나무자동화

Tree automaton
나무 자동화에 대한 다른 개념은 나무 자동화를 참조하십시오.

나무자동차는 상태기계의 일종이다.나무 오토마타는 더 전통적인 상태 기계의 현이 아닌 나무 구조를 다룬다.

다음 기사는 나뭇가지 나무 오토마타를 다루고 있는데, 이것은 나무의 정규 언어에 해당한다.

고전적인 자동화와 마찬가지로 유한 나무 자동화는 결정론적 자동화가 될 수도 있고 아닐 수도 있다.자동화가 입력 트리를 처리하는 방식에 따라 유한 나무 자동화는 (a) 바닥 위로, (b) 위 아래로 두 가지 유형으로 구성될 수 있다.이것은 중요한 문제인데, 비결정론적 (ND) 하향식 자동화와 ND 상향식 트리 자동화는 표현력이 동일하지만 결정론적 하향식 자동화는 결정론적 상향식 자동화에 비해 절대적으로 덜 강력하다. 왜냐하면 결정론적 하향식 자동화는 결정론적 하향식 트리 자동화에 의해 지정된 트리 특성은 경로 받침대에만 의존할 수 있기 때문이다.에르티. (결정론적인 상향식 트리 자동화는 ND 트리 자동화와 같이 강력하다.)

정의들

F에 대한 상향식 유한 나무 automaton 주의는 집합 투플(Q, F, Qf, Δ),, F는 위치를 차지하고 알파벳(즉, 알파벳의 기호 연결된 arity다), 막바지 상태의 Qf ⊆는 집합 형태 f(q1(x1)의 전환 규칙,...,qn(xn))→ q(f(x1,...,xn)cmΔ 있는,n-ary f에 ∈ F, q키 ∈ Q, 크시 초본으로 정의된다.iables면 끝나.오팅 하위 트리즉, Δ의 구성원은 자식들의 뿌리가 상태인 노드부터, 뿌리가 상태인 노드까지 규칙을 다시 쓰는 것이다.따라서 노드의 상태는 그 자식들의 상태에서 추론된다.

n=0, 즉 상수 기호 f의 경우 위의 전환 규칙 정의는 f() → q()로 읽는다. 편의를 위해 빈 괄호를 생략하는 경우가 많다. f → q(f)상수 기호(리브)에 대한 이러한 전환 규칙에는 상태가 필요하지 않으므로 명시적으로 정의된 초기 상태는 필요하지 않다.상향식 트리 자동화는 모든 잎에서 동시에 시작하여 위쪽으로 이동하여 각 하위 용어와 Q의 런 상태를 연관시킨다.이 용어는 그 근원이 Q부터f 수용 상태와 연관되어 있는 경우 받아들여진다.[1]

F에 대한 하향식 유한 나무 자동화는 투플(Q, F, Qi, Δ)로 정의되며, 상향식 나무 자동화와 두 가지 차이가 있다.첫째, 초기 상태의 집합인 Qi ⊆ Q는 Q를f 대체하고, 둘째, 그 전환 규칙은 q(x1, ...xn) → f(q11), q(x), qn(xn), q(x), q(x)의 역방향으로, n-ary f variables F, q, qi(x) 및 x 변수가i 하위 트리를 나타낸다.즉, Δ의 구성원들은 여기서 뿌리가 상태인 노드부터 아이들의 뿌리가 상태인 노드까지 규칙을 다시 작성한다.하향식 자동화는 루트 초기 상태의 일부에서 시작하여 각 하위 용어와 런 상태를 따라 연결하면서 트리의 가지를 따라 아래로 이동한다.모든 나뭇가지가 이런 식으로 통과할 수 있다면 나무는 인정된다.[2]

나무 자동화를 결정론적(약칭 DFTA)이라고 하는데, 만일 Δ의 두 규칙이 동일한 왼손 측면을 가지고 있지 않다면, 나무 자동화를 비결정론적(약칭 DFTA)이라고 한다.[3]비결정론적인 하향식 나무 오토마타는 비결정론적인 상향식 나무와 같은 표현력을 가지고 있다;[4] 전환 규칙은 간단히 뒤바뀌고 최종 상태는 초기 상태가 된다.

이와는 대조적으로, 결정론적 하향식 트리 오토마타는[5] 상향식 트리 오토마타보다 덜 강력하다. 결정론적 트리 오토마토에서는 두 전환 규칙이 동일한 좌측을 가지지 않기 때문이다.트리 오토마타의 경우 전환 규칙은 다시 쓰기 규칙이며, 하향식 규칙의 경우 왼쪽은 상위 노드가 된다.따라서 결정론적 하향식 트리 자동화는 모든 분기에서 참인 트리 특성에 대해서만 테스트할 수 있을 것이다. 각 자식 분기에 쓸 상태의 선택은 하위 분기의 내용을 알지 못한 채 상위 노드에서 결정되기 때문이다.

예

상향식 자동 허용 부울 목록

F와 Q의 멤버를 구별하기 위해 색소를 사용하고, arity 2와 arity 0의 다른 모든 기호를 가진 순위 알파벳 F={ false, true,nil,cons(,.)}를 사용하여 모든 유한한 부울 값 리스트 집합을 수용하는 상향식 트리 자동화를 Q={Bool,{Bool,{Bool)와 함께 (Q, F, Ff, Q, Δ)로 정의할 수 있다.규칙으로f 구성된 BList }, Q={ BList }, Δ

거짓의 → 불(거짓) (1),
진실의 → 불(참) (2),
못을 박다 → 블리스트(nil) (3) 및
cons(Bool(x1),BLISt(x2) → BList(cons(x1,x2)) (4).

이 예에서 규칙은 각 용어에 상향식으로 그 유형을 할당하는 것으로 직관적으로 이해할 수 있다. 예를 들어 규칙 (41)은 "x1,x는2 bool, x는 blist를 가지고 있다. 단2, x는 bool, blist를 각각 가지고 있다."로 읽을 수 있다.허용 가능한 실행 예는 다음과 같다.

단점 거짓, 단점 사실이야 못을 박다 ))
⇒ 단점 거짓, 단점 사실이야 블리스트(nil) )) (3)로
⇒ 단점 거짓, 단점 Bool(참), 블리스트(nil) )) (2)로
⇒ 단점 거짓, BLISt(컨설팅) 사실이야 못을 박다 ))) (4)로
⇒ 단점 Bool(거짓말), BLISt(컨설팅) 사실이야 못을 박다 ))) (1)로
⇒ BLISt(컨설팅) 거짓, 단점 사실이야 못을 박다 ))) (4)에 의해 승인된다.

Cf. 일반 나무 문법에 나타난 자동화에 해당하는 일반 나무 문법에서 같은 용어의 유래#예.

거부 예제 런은

단점 거짓, 진실의 )
⇒ 단점 거짓, 불(참) ) (1)로
⇒ 단점 Bool(거짓말), 불(참) ) (2) 더 이상의 규정은 적용되지 않는다.

직관적으로 이것은 cons(허위, 참)라는 용어가 잘 활자화되지 않는 것에 해당한다.

2진수 표기법에서 3의 배수를 허용하는 하향식 자동화

(A) (B) (C) (D)
끈
문법
규칙. 		끈
오토매틱
전환 		나무
오토매틱
전환 		나무
문법
규칙.
0
1
2
3
4
5
6
S0 → ε
S0 → 0 S0
S0 → 1 S1
S1 → 0 S2
S1 → 1 S0
S2 → 0 S1
S2 → 1 S2
Δ(S0,0) = S0
Δ(S0,1) = S1
Δ(S1,0) = S2
Δ(S1,1) = S0
Δ(S2,0) = S1
Δ(S2,1) = S2
S0(nil) → 못을 박다
S0(0)(x) → 0(S0(x))
S0(1(x)) → 1(S1(x))
S1(0)(x) → 0(S2(x))
S1(1(x)) → 1(S0(x))
S2(0)(x) → 0(S1(x))
S2(1(x)) → 1(S2(x))
S0 → 못을 박다
S0 → 0(S0)
S0 → 1(S1)
S1 → 0(S2)
S1 → 1(S0)
S2 → 0(S1)
S2 → 1(S2)
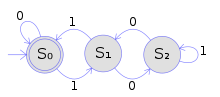이항 표기법에서 3의 배수를 수용하는 결정론적 유한(끈) 자동

위와 동일한 색상을 사용하여, 이 예는 나무 자동화가 일반 문자열 자동화를 어떻게 일반 문자열 자동화하는지를 보여준다.그림에 표시된 유한 결정론적 문자열 자동화는 3의 배수를 나타내는 이진수의 모든 문자열을 허용한다.결정론적 유한 자동#형식 정의의 개념을 사용하여 다음과 같이 정의한다.

  • 상태0 설정 Q는 { S, S, S12 },
  • 입력 알파벳: { 0, 1 },
  • 초기 상태는 S0,
  • 최종 상태 집합은 {S0}이고
  • 표의 열(B)에 표시된 것과 같은 전환

트리 자동 설정에서 입력 알파벳이 변경되어 기호 0과 1이 모두 단항이고, 나무 잎에 nil을 사용한다고 하는 무효 기호가 된다.예를 들어 문자열 자동 설정의 이진 문자열 "110"은 트리 자동 설정의 "1(1(0(nil))""에 해당하며, 이렇게 하면 문자열을 나무 또는 용어로 일반화할 수 있다.이항 문자열 표기법에서 3의 배수에 해당하는 모든 용어의 집합을 허용하는 하향식 유한 트리 자동화는 다음에 의해 정의된다.

  • 상태 설정 Q는 여전히 { S0, S, S12 },
  • 순위 입력 알파벳은 {0, 1, nil }이며, 설명과 같이 Arity(0)=Ariity(1)=1 및 Arity(nil)=0이 있다.
  • 초기 상태 집합은 {S0}이고
  • 표의 열(C)에 표시된 것과 같은 전환

예를 들어, "1(0(nil)" 트리는 다음과 같은 트리 자동 실행으로 허용된다.

S0() 1( 1( 0( 못을 박다 ))))
⇒ 1( S1() 1( 0( 못을 박다 )))) 2시까지
⇒ 1( 1( S0() 0( 못을 박다 )))) 4시까지
⇒ 1( 1( 0( S0() 못을 박다 )))) 1로
⇒ 1( 1( 0( 못을 박다 ))) 0로

반대로 "1(0(nil)"이라는 용어는 승인되지 않은 자동 실행을 다음과 같이 이끈다.

⇒ S0() 1( 0( 못을 박다 )))
⇒ 1( S1() 0( 못을 박다 )))) 2시까지
⇒ 1( 0( S2() 못을 박다 )))) 3시까지, 더 이상의 규칙은 적용되지 않는다.

자동운전을 시작할 초기 상태는 S0 외에 없기 때문에, 나무 자동화에 의해 "1(0(nil)"이라는 용어는 받아들여지지 않는다.

비교를 위해 표는 각각 자동문법과 동일한 언어를 수용하는 컬럼 (A)와 (D)에 각각 (우)정규(현)문법과 일반 나무문법을 제공한다.

특성.

인식성

상향식 자동화의 경우 t(t)에서 시작하여 q(t)로 끝나는 감소가 존재한다면 t(즉, 트리)라는 용어가 허용된다. 여기서 q는 최종 상태다.하향식 자동화의 경우, q(t)에서 시작하여 t로 끝나는 감소가 존재하는 경우, q가 초기 상태일 때 t를 허용한다.

나무 자동 A에 의해 인정되거나 인정된 나무 언어 L(A)은 A가 인정하는 모든 지상 용어들의 집합이다.지면 용어 세트는 그것을 받아들이는 나무 자동화가 존재한다면 알아볼 수 있다.

선형(즉, 경락을 보존하는) 나무 동형성은 인식성을 보존한다.[6]

완전성 및 감소

모든 가능한 기호 상태 조합에 사용 가능한 전환 규칙이 하나 이상 있는 경우 비결정론적 유한 나무 자동화가 완료된다.상태 q는 t에서 q(t)로 감소하는 기초 용어 t가 존재하는 경우 접근할 수 있다.NFTA는 모든 주에 접근할 수 있으면 축소된다.[7]

펌핑 보조정리

인식 가능한 트리 언어 L에서 충분히 큰[8] 모든 지상 용어 t는 중간 부분의 임의 반복("펌핑")이 결과 용어를 L로 유지하도록 수직으로 3분할[9] 수 있다.[10][11]

위의 예에서 나온 모든 유한 부울 값 목록의 언어의 경우, 높이 제한 k=2를 초과하는 모든 항은 단점 발생을 포함해야 하므로 펌핑할 수 있다.예를 들면.

반대(거짓말, cons(진실, nil) ) ,
반대(거짓말), 반대(허위), cons(진실, nil) )) ,
동의(거짓말), 동의(거짓말), 동의(거짓말), cons(진실, nil) ))) , ...

모두 그 언어에 속한다.

폐쇄

인지할 수 있는 트리 언어의 클래스는 결합, 보완, 교차점에 따라 폐쇄된다.[12]

마이힐-네로드 정리

순위에 따른 알파벳 F에 대한 모든 나무 집합의 합치는 u1 ≡ v와1 ...와 un vn v가 모든 f every F에 대해 f(u1,...,un) f f(v1,...,vn)를 암시하는 등가관계다.등가 등급의 수가 유한할 경우 지표가 유한하다.

주어진 트리 언어 L의 경우, 각 컨텍스트 C에 대해 C[u] ∈ L if C[v] if L이면 u Lv로 합치를 정의할 수 있다.

나무 오토마타에 대한 마이힐-네로드 정리는 다음과 같은 세 가지 문장이 동등하다고 명시하고 있다.[13]

  1. L은 인식 가능한 트리 언어다.
  2. L은 유한 지수의 합성에 대한 일부 동등성 등급의 결합이다.
  3. 관계 ≡L은 유한 지수의 합이다.

참고 항목

메모들

  1. ^ 코몬 외 2008, 제1.1장, 페이지 20.
  2. ^ 코몬 외 2008, 1.6장, 페이지 38.
  3. ^ 코몬 외 2008, 제1.1장, 페이지 23.
  4. ^ Comon 등 2008, 1.6장, 정리 1.6.1, 페이지 38.
  5. ^ 엄격한 의미에서 결정론적 하향식 자동화는 코몬 외 연구진에 의해 정의되지 않는다. (2008) 그러나 그들은 그곳에서 사용된다(1.6절, 제안서 1.6.2, 페이지 38).그들은 경로 폐쇄형 트리 언어의 등급(섹션 1.8, 연습 1.6, 페이지 43-44)을 받아들인다.
  6. ^ 코몬 등의 개념. 나무 동형주의(2008, 1.4, 정리 1.4.3, 페이지 31-32)는 "나무 동형주의"의 그것보다 더 일반적이다.
  7. ^ 코몬 외 2008, 제1.1장, 페이지 23-24.
  8. ^ 형식: 높이(t) > k, k > 0은 L에만 의존하고 t에는 의존하지 않는다.
  9. ^ 형식: c[.], context C'[.], t = C[C][u]와 같은 ground term u가 있다."콘텍스트" C[.]]는 하나의 구멍이 있는 나무(또는 그에 상응하여 하나의 변수가 발생하는 항)이다.트리가 홀 노드(또는 해당 용어가 변수일 경우)로만 구성된 경우 컨텍스트를 "티비얼"이라고 한다.표기 C[t]는 C[t]의 구멍에 나무 t를 삽입한 결과(또는 그에 상응하여 변수를 t로 인스턴스화)를 의미한다.코몬 외 2008, 페이지 17은 공식적인 정의를 내린다.
  10. ^ 형식: C[C][nu] ∈ L 전체 n ≥표기법n C[ α]는 C[ α]의 복사본 n개를 다른 복사본, cf에 쌓은 결과를 의미한다.코몬 외 2008년, 페이지 17.
  11. ^ 코몬 외 2008, 제1.2장, 페이지 29.
  12. ^ 코몬 외 2008, 1.3장 정리 1.3.1, 페이지 30.
  13. ^ 코몬 외 2008, 1.5장, 페이지 36.

참조

  • Comon, Hubert; Dauchet, Max; Gilleron, Rémi; Jacquemard, Florent; Lugiez, Denis; Löding, Christof; Tison, Sophie; Tommasi, Marc (November 2008). Tree Automata Techniques and Applications (PDF). Retrieved 11 February 2014.
  • Hosoya, Haruo (4 November 2010). Foundations of XML Processing: The Tree-Automata Approach. Cambridge University Press. ISBN 978-1-139-49236-2.

외부 링크

구현

  • Grappa - 랭킹 및 랭킹이 없는 트리 자동 라이브러리(OCaml)
  • Timbuk - 도달 가능성 분석 및 나무 자동 계산(OCaml)을 위한 도구
  • REACH - 유한 나무 및 헤지 오토마타 작업을 위한 라이브러리(Java)
  • 기계 점검 트리 오토마타 라이브러리(Isabelle [OCaml, SML, Haskell])
  • VATA - 비결정적 트리 오토마타(C++)의 효율적인 조작을 위한 라이브러리