횡단(계기 제작)
Transversal (instrument making)횡단면은 졸업식을 보다 정밀하게 읽을 수 있도록 과학적인 기구에 기하학적 구조를 말한다.현대에는 횡단면이 버니어 비늘로 대체되었다.이 방법은 인터셉트 정리(탈레스의 정리라고도 한다)에 근거한다.
역사
정교하게 채색된 악기를 만들기 어려운 시기에 횡단기를 사용하였다.그것들은 14세기 초부터 악기에서 발견되었지만, 발명가는 알려져 있지 않다.1342년 Levi Ben Gerson은 Jacob의 스태프라고 불리는 악기를 도입하여(Jacob Ben Makir가 전 세기를 발명한 것으로 보인다) 언급된 악기에 적용되는 횡단 축척의 방법을 설명했다.[1][2]
토마스 디지스는 횡단적 규모의 발견을 항해사 겸 탐험가 리처드 챈슬러(일부 저자들이 시계 제작자와 다른 이름, 그 중 다음과 같은 이름으로 칭함)의 탓으로 잘못 돌렸다.리처드 [3][4][5][6][7][8]챈슬러 또는 리처드 칸츨러).그것은 16세기 후반에야 천문학 기구에 쓰이기 시작했다.Tycho Brahe는 그것들을 사용했고 그 기술을 대중화하기 위해 많은 것을 했다.[9][10]이 기술은 피에르 베르니에가 이 기술을 도입한 지 1세기가 지난 18세기 후반에 버니어가 보편화되면서 사라지기 시작했다.
트랜스버스와 버니어 눈금 사이의 중간에는 페드로 누네스에 의해 개발된 노니우스 시스템이 사용되었다.하지만, 그것은 결코 흔한 일이 아니었다.타이코도 노니우스 방법을 사용했지만, 그렇게 한 유일한 저명한 천문학자로 보인다.
선형 횡단
선형 횡단면들은 선형 눈금에 사용되었다.선 그리드는 선형 눈금에 바로 인접하여 작성되었다.눈금 위로 뻗은 선들이 그리드의 일부를 형성했다.그리드에서 확장된 졸업선에 수직인 라인 수는 계기 제작자가 제공하고자 하는 정밀도의 정도에 따라 달라졌다.
5행의 격자는 졸업생의 5분의 1로 측정치를 결정할 수 있다.10줄의 격자는 10분의 1을 측정할 수 있다.선 사이의 거리는 거리가 정확하게 균일한 한 중요하지 않다.거리가 길수록 정확도가 높아진다.
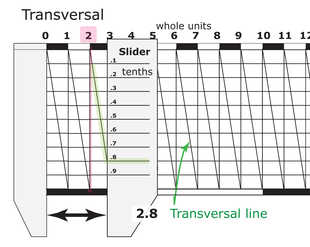
오른쪽 그림에서 보듯이 일단 그리드를 스크리빙하면, 대각선(횡단선)은 그리드의 기둥 상단 모서리에서 반대쪽 가장 낮은 모서리로 스크리빙되었다.이 선은 격자의 교차선을 등간격으로 교차한다.커서, 알리데이드 또는 유사한 측정 지표를 사용하여 횡단면이 그리드를 가로지르는 가장 가까운 지점을 결정한다.그것은 그 조치의 졸업의 분수를 나타낸다.
그림에서 판독치는 수직 빨간색 선으로 표시된다.이것은 알리데이나 비슷한 장치의 가장자리가 될 수 있다.커서가 위에서 네 번째 격자선에 가장 가까운 횡단면을 가로지르기 때문에 판독치(가장 왼쪽 긴 졸업선이 0.0이라고 가정)는 0.54이다.
원형 횡단
원형 횡단보도는 원형 호를 제외하고 선형 횡단보도와 동일한 기능을 수행한다.이 경우, 그리드의 건설은 훨씬 더 복잡하다.직사각형 격자는 작동하지 않을 것이다.방사형 선과 원주 호 그리드를 생성해야 한다.또한 선형 횡단선은 방사형 그리드를 동일한 세그먼트로 분할하지 않는다.원형 호 세그먼트는 정확한 비율을 제공하기 위해 횡단형으로 구성되어야 한다.
타이코 브라헤
Tycho Brahe는 두 개의 잘린 사지를 형성하는 두 그룹의 호 사이에 세컨트로 만들어진 횡단선 격자를 만들었다.세컨트는 사지의 분할을 다른 사지의 다음 분할과 결합하여 그려진다(티코 브라헤의 사분면 2도 배율 반경 2m의 그림 참조).[9]
그는 각 도마다 "V"를 형성하는 대체 모드에서 6개의 직선 횡단면을 그렸고, 각각의 횡단면은 10개의 부분으로 나눈 9개의 점으로 구성되었고, 6에 60분을 곱했다.[11]압드 알 문알 아밀레(16세기)는 모두 같은 방향으로 그렸지만(그의 악기는 정밀도가 떨어지지만)는 모두 같은 방향으로 그렸다.[12]
기타저작
천문학적, 지리학적 기구에서 원형 또는 반원형의 사지 각도의 측정에 적용되는 "직선 횡단"의 방법은 여러 저자에 의해 다루어졌다.이 시스템의 정확성을 연구하면서, 그들 중 일부는 "직선 횡단" 대신 "순환 횡단"을 사용하는 것이 편리함을 나타냈다.[13]
참고 항목
참조
- ^ Bernard R. Goldstein (6 December 2012). The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Springer Science & Business Media. pp. 164–. ISBN 978-1-4613-8569-1.
- ^ Brian Lasater (2008). The Dream of the West, Pt II. Lulu.com. pp. 355–. ISBN 978-1-4303-1382-3.
- ^ Thomas Digges (1573). Alae seu scalae mathematicae, quibus visibilium remotissima coelorum theatra conscendi, & planetarum omnium itinera nouis & inauditis methodis explorari: ... Thoma Diggeseo, ... authore. pp. 86–.
- ^ Joseph Needham (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 296–. ISBN 978-0-521-05801-8.
- ^ Jean Baptiste Joseph Delambre (1819). Histoire de l'astronomie du moyen age; par m. Delambre, chevalier de Saint-Michel et de la Legion-d'honneur . mme ve Courcier, imprimeur-libraire pour les sciences. pp. 372–.
- ^ Aimé Laussedat (1898). Recherches sur les instruments: Aperçu historique sur les instruments et les méthodes. La topographie dans tous les temps. Gauthier-Villars.
- ^ Maurice Daumas (1953). Les Instruments scientifiques aux XVIIe et XVIIIe siècles. Presses Universitaires de France.
- ^ A.D. Morrison-Low (2 March 2017). Making Scientific Instruments in the Industrial Revolution. Taylor & Francis. pp. 61–. ISBN 978-1-351-92074-2.
- ^ a b Tycho Brahe (1946). Tycho Brahe's description of his instruments and scientific work: as given in Astronomiae instauratae mechanica (Wandesburgi 1598). I Kommission hos E. Munksgaard.
- ^ John Louis Emil Dreyer (13 February 2014). Tycho Brahe. Cambridge University Press. pp. 58–. ISBN 978-1-108-06871-0.
- ^ Tycho Brahe (1602). Tychonis Brahe-Astronomiæ instauratæ mechanica. Noribergae [Nürnberg]: Levinum Hvlsivm.
- ^ The Instruments of Istanbul Observatory (1977). The Instruments of Istanbul Observatory. p. 108.
- ^ Allain Manesson-Mallet (1702). La Geometrie pratique: Tome second. Contenant la trigoniometrie, ou la mesure des distances par les instrumens geometriques ... chez Anisson directeur de l'Imprimerie Royale. pp. 32–.
참고 문헌 목록
- 다음아스, 모리스, 17, 18세기의 과학 악기들과 그들의 제작자들, 포트만 북스, 런던 1989 ISBN 978-0-7134-0727-3
외부 링크
| 위키미디어 커먼즈에는 노모그램과 관련된 미디어가 있다. |