초해상도 광학변동영상화

초고해상도 광학변동영상(SOFI)은 독립적으로 변동하는 형광 방출기의 시간적 상관관계를 바탕으로 기록된 영상 시계열에서 초해상 영상을 계산하기 위한 후처리 방법이다.

SOFI는 독립적으로 변동하는 형광 방출체(유기 염료, 형광 단백질)로 라벨이 부착된 생물학적 시료의 초해상도용으로 개발됐다.단일 분자 로컬리제이션에 의존하여 회절 제한 영역(DLA) 및 시점당 하나의 활성 분자만 허용하는 SCON 또는 PALM과 같은 다른 초해상도 현미경 기법에 비해 SOFI는 긴 영상 시간뿐만 아니라 제어된 광스위치 및/또는 광 활성화가 필요하지 않다.^[1][2][3][4]그럼에도 불구하고, 그것은 실제 온/오프 상태 또는 형광 강도가 다른 상태 중 두 가지 구별 가능한 상태를 순환하는 불소포어를 요구한다.수학적 용어로 SOFI 이미징은 두 가지 구별 가능한 방법이 존재하는 경우 적산물의 계산에 의존한다.하나는 정의상 각 픽셀 자체의 정보에만 의존하는 자동 큐뮬런트를^[3] 통해 영상을 계산할 수 있고, 다른 하나는 개선된 방법이 교차 큐뮬런트의 계산을 통해 서로 다른 픽셀의 정보를 활용한다.^[5]두 방법 모두 누적 계산에는 한계가 있지만 최종 영상 분해능을 크게 높일 수 있다.실제로 SOFI는 3차원 모두 해상도를 높일 수 있다.^[3]

원리

다른 초해상도 방법과 마찬가지로 SOFI는 CCD- 또는 CMOS 카메라에 영상 시리즈를 기록하는 것에 기초한다.다른 방법과는 달리, 방출체의 정확한 국산화 작업이 필요하지 않으므로, 기록된 시계열은 회절 제한 면적당 더 많은 양의 활성 불소 형상이 허용되기 때문에 실질적으로 더 짧을 수 있다.n번째 순서의 SOFI-이미지의 픽셀 값은 n번째 순서 누적분 형태의 픽셀 시계열 값에서 계산되는 반면, 픽셀에 할당된 최종 값은 상관함수에 대한 적분으로 상상할 수 있다.마지막으로 할당된 픽셀 값 강도는 형광 신호의 밝기 및 상관 관계를 측정한 것이다.수학적으로 n번째 순서 누적분은 n번째 순서 상관 함수와 관련이 있지만, 결과적인 이미지 분해능과 관련하여 몇 가지 장점을 보인다.SOFI에서는 DLA당 여러 개의 방출체가 허용되므로, 각 픽셀의 광자 카운트는 근처에 활성화된 모든 방출체의 신호의 중첩에서 발생한다.누적된 계산은 이제 신호를 걸러내고 높은 상관 관계가 있는 변동만을 남긴다.이것은 대조도 향상을 제공하고 따라서 좋은 측정을 위한 배경 축소를 제공한다.왼쪽 그림에서 암시하듯이 형광원 분포:

${\displaystyle \sum _{k=1}^{N}\delta ({\vec{r}-{r}_{k}}\vecdot \varepsilon _{k}\cdot s_{k}(t)}}$

시스템의 포인트 스프레드 기능(PSF) U(r)와 함께 해결된다.따라서 시간 t 및 위치 $r{\displaystyle \stackrel{}{}}$→ ${\$에서 형광 신호가 제공됨$$

${\displaystyle F({\vec {r},t)=\sum _{k=1}^{{n}U({\vec {{r}-{r}_{k}}\cdot \varepsilon _{k}}(t).}$

위의 방정식 내에서 N은 $시간$에 ${\displaystyle {따른}_{}}$ 분자 밝기 ${\displaystyle {\epsilon }_{}}$ k${\displaystyle {}_{}}\epsilon {\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\epsilon }_{}}$ k ${\$$displaystyle{\vec}_{k}}}{\$$displaystyle \varepsilon _{k}}}}}$에 위치한 방출체의 양이며, 여기서$$ $\epsilon {\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$은 일정한$$ 분자 brig의 변수다.tness and $s{\displaystyle {}_{}}$ ${\displaystyle k_{}}$( ${\displaystyle t}$) ${\displaystyle s_{k}(t)}$은 시간변동변동함수다.분자 밝기는 단지 형광 계수 평균을 특정 지역 내의 분자 수로 나눈 것이다.단순화를 위해 표본이 고정 평형 상태여서 형광 신호는 0-평균 변동으로 표현될 수 있다고 가정해야 한다.

${\displaystyle \delta F({\vec {r},t)=F({\vec{r},t)-\langle F({\vec{r},t)\angle _{t}}$

여기서 $⟨{\displaystyle }$ ${\displaystyle {}_{}}$ ${\displaystyle t_{}}$ t ${\$은 시간 평균을 나타낸다$$.여기서의 자동 상관관계(예: 2차 주문)는 특정 시간 지연 $\tau {\displaystyle }$ ${\displaystyle \tau }$에 대해 다음과 같이 연역적으로 설명할 수 있다$.$

${\displaystyle \delta F({\vec {r},t)=\langle \delta F({\vec {r},t+\tau )\cdot \delta F({\vec {r},t)\rangele _{t}}}}$

이러한 방정식에서 광학 시스템의 PSF는 상관관계의 순서에 따라 힘을 얻어야 한다.따라서 2차 상관 관계에서 PSF는 $2{\displaystyle \sqrt{\mathrm{}}}$ ${\$}의$$인수만큼 모든 차원에 따라 감소할 것이다$.$ 그 결과 SOFI 이미지의 분해능은 이 인자에 따라 증가한다.

누적분포함수 대 상관 계수

픽셀 값의 재할당을 위해 단순 상관 함수만 사용하면 교차 상관 용어가 새로운 픽셀 값에 기여하지 않는 방식으로 적시에 방출자의 변동이 독립적이기 때문이다.고차 상관 함수의 계산은 저차 상관 관계 항이 모두 사라지기 때문에 어떤 이유로 적산물을 계산하는 것이 우수한지에 대한 저차 상관 관계 때문에 어려움을 겪을 수 있다.

누적 계산

오토큐뮬런트

계산상의 이유로 고차 응고제의 모든 시간 지연을 0으로 설정하는 것이 편리하여 n번째 순서 자동 응고제에 대한 일반적인 표현을 찾을 수 있다.^[3]

${\displaystyle AC_{n1}({\vec{r},\tau _{1\ldots n-1}=0)=\sum _{k=1}{{n1}U^{n}({\vec{r}_{k})\varepsilon _{k}{nw_{n}{k}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"$

${\displaystyle w_{}}$ ${\displaystyle k_{}}$ ${\$는 적산물의 순서에 영향을 받고 주로 방출체의 변동 특성에 따라 영향을 받는 특정한 상관관계에 기초한 가중치 함수다$$.

적산물의 매우 높은 순서를 계산하여 PSF의 FWHM을 축소하는 데는 근본적인 제한이 없지만, 최종 이미지에 할당된 값의 가중치에 따라 실질적인 한계가 있다.분자 밝기가 높은 방출체는 고차에서 할당된 픽셀 누적값의 측면에서 강한 증가를 보일 것이며, 이 성능은 다양한 방출체의 변동으로 기대할 수 있다.따라서 결과 영상의 광범위한 강도 범위를 예상할 수 있으며, 결과적으로 흐릿한 방출체가 고차 영상에서 밝은 방출체에 의해 가려질 수 있다.^[3][5]자동 응고제의 계산은 수학적인 의미에서 매우 매력적인 방법으로 실현될 수 있다.n번째 순서 누적분은 순간의 기본^[6] 반복으로 계산할 수 있다.

${\displaystyle K_{n}({\vec {r}})=\mu _{n}({\vec {r}})-\sum _{i=1}^{n-1}{\begin{pmatrix}n-1\\i\end{pmatrix}}K_{n-i}({\vec {r}})\mu _{i}({\vec {r}})}$

여기서 K는 지수 순서의 누적분이며, 마찬가지로 $\mu {\displaystyle }$ ${\displaystyle \mu }$은 순간들을 나타낸다$$.괄호 안의 항은 이항계수를 나타낸다.이러한 계산 방법은 표준 공식으로 적산물을 계산하는 것과 비교하면 간단하다.계산 시간이 얼마 남지 않은 적출액 계산이 가능하며, 잘 구현된 만큼 대형 영상에서 고차적 적출액 계산에도 적합하다.

크로스큐뮬란트

보다 진보된 접근법에서 교차 큐뮬런트는 몇 픽셀의 정보를 고려하여 계산된다.교차 응고제는 다음과 같이 설명할 수 있다.^[5][7]

${\displaystyle CC_{n}({\vec {r}},\tau _{1\ldots n-1}=0)=\prod _{j<l}^{n}U{\Bigg (}{\frac {{\vec {r}}_{j}-{\vec {r}}_{l}}{\sqrt {n}}}{\Bigg )}\cdot \sum _{i=1}^{N}U^{n}{\Bigg (}{\vec {r}}_{i}-{\frac {\sum _{k}^{n}{\vec {r}}_{k}}{n}}{\Bigg )}\varepsilon _{i}^{n}w_{i}(0)}$

j, l, k는 기여 픽셀에 대한 지수인 반면 나는 현재 위치에 대한 지수인 것이다.다른 모든 값과 지수는 이전과 같이 사용된다.이 방정식과 자동 응고제 방정식의 비교에서 주요한 차이는 가중 $인자{\displaystyle }$ U${\displaystyle }$(${\displaystyle r_{}}$ j${\displaystyle {}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle l\sqrt{}{}_{}}$/ n$){\displaystyle U(r_{j}-r_{l}/{\sqrt{n}}}}}$의 출현이다$.$이 가중-요인(거리-요인이라고도 함)은 PSF형이며, 각 픽셀의 기여도가 거리를 따라 PSF형식으로 감소한다는 점에서 교차 상관관계 픽셀의 거리에 의존한다.원칙적으로 이는 거리 요인이 더 멀리 떨어져 있는 픽셀의 경우 더 작다는 것을 의미한다.교차 큐뮬런트 접근방식은 효과적인 픽셀 크기를 줄임으로써 라벨링된 시료에 대한 진정한 정보를 보여주는 새로운 가상 픽셀을 만드는 데 사용될 수 있다.이 픽셀들은 단순한 보간술에서 발생하는 픽셀보다 더 많은 정보를 가지고 있다.

또한 앞서 언급한 것처럼 교차 상관에서 "손실"로 인한 가상 픽셀의 강도 차이를 이용하여 광학 시스템의 PSF를 추정할 수 있다.^[5]각 가상 픽셀은 픽셀의 거리 인자 역률로 재가중할 수 있어 진정한 누적값의 복원이 가능하다.마지막으로 PSF를 사용하여 "광학적 전달 함수"(OTF)를 재가중하여 n번째 순서 누적분에 대한 n번째 분해능 종속성을 생성할 수 있다.^[5]또한 이 단계는 더 적은 계산 비용과 관련된 디콘볼루션에 PSF를 사용하는 것으로 대체될 수 있다.

교차 계산은 파티션에 대한 합계의 계산을 구성하는 훨씬 더 비싼 계산식을 사용해야 한다.이것은 물론 새로운 값을 할당하기 위해 다른 픽셀의 조합에 기인한다.따라서 이 시점에서는 빠른 재귀적 접근법을 사용할 수 없다.교차 큐뮬런트의 계산에는 다음과 같은 방정식을 사용할 수 있다.^[8]

${\displaystyle K_{n}{\vec{r}={\frac{1}{n}}\sum _{i=1}^{n}{\vec {r_{i}}}{\Bigg )}=\sum _{P}-1(P -1)^{P -1}(P -1)!\prod _{p\in P}{\Big \langle }\prod _{i\in p}F({\vec{r}})_{i}{\Big \rangele }_{t}}}}$

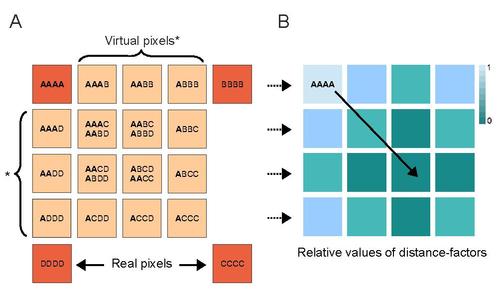
이 방정식에서 P는 가능한 파티션의 양을 나타내며, p는 각 파티션의 다른 부분을 나타낸다.또한 i는 계산 중에 고려된 여러 픽셀 위치에 대한 인덱스로서 F에 대한 것은 기여하는 여러 픽셀의 영상 스택일 뿐이다.교차큐뮬런트 접근방식은 앞서 언급한 적층물의 순서에 따라 가상 픽셀의 생성을 촉진한다.이러한 가상 픽셀은 4차선 교차 큐뮬런트 영상에 대한 원본 픽셀에서 특정 패턴으로 계산할 수 있으며, 하단 이미지인 파트 A에 묘사되어 있다.패턴 자체는 원본 영상 픽셀 A, B, C 및 D의 가능한 모든 조합의 계산에서 단순하게 발생한다.여기서 이것은 "반복과 결합"의 계획에 의해 이루어졌다.가상 픽셀은 상관 관계 자체로 인한 강도 손실을 나타낸다.두 번째 이미지의 파트 B는 교차 상관에 있는 가상 픽셀의 일반적인 의존성을 묘사한다.의미 있는 픽셀 값을 복원하기 위해 가상 픽셀 그리드의 각 픽셀에 대한 거리 요소를 PSF 모양으로 정의하고 동일한 거리 요인과 관련된 모든 이미지 픽셀에 반전을 적용하는 루틴에 의해 영상이 평활화된다.^[5][7]

참조