슬라이스 샘플링

슬라이스 샘플링은 의사 난수 샘플링을 위한 마르코프 체인 몬테카를로 알고리즘의 일종으로, 즉 통계적 분포에서 랜덤 표본을 추출하기 위한 것이다.이 방법은 랜덤 변수를 표본으로 추출하기 위해 밀도 함수의 그래프 아래 영역에서 균일하게 표본을 추출할 수 있다는 관측에 기초한다.^[1][2][3]

동기

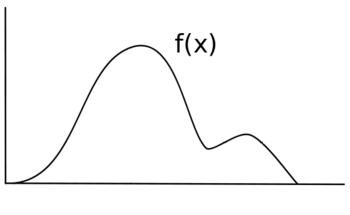
분포 f(x)를 사용하여 일부 랜덤 변수 X를 표본으로 추출한다고 가정합시다.다음은 f(x)의 그래프라고 가정해 보자.f(x)의 높이는 그 지점에서의 가능성과 일치한다.

X를 균일하게 표본으로 추출할 경우 각 값은 표본 추출 가능성이 동일하며 분포는 일부 불균일 함수 f(x) 대신 일부 y 값에 대해 f(x) = y 형식이 될 것이다.원래 검은색 선 대신, 당신의 새로운 분포는 파란 선과 더 비슷할 것이다.

분포 f(x)를 유지하는 방법으로 X 표본을 추출하기 위해서는 f(x)의 각 범위에 대한 다양한 가능성을 고려하는 일부 표본 추출 기법을 사용해야 한다.

방법

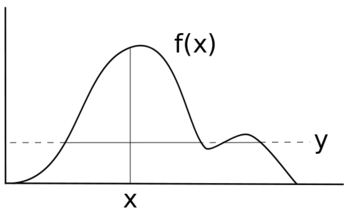
가장 간단한 형태의 슬라이스 샘플링은 다음과 같이 어떤 점도 기각할 필요 없이 곡선 f(x) 아래에서 균일하게 샘플을 추출한다.

1. f(x₀)가 0보다 큰 시작 값 x를₀ 선택하십시오.
2. 샘플 ay0과 f(x₀) 사이의 값이 균일하다.
3. 이 때 곡선을 가로지르는 수평선 그리기y위치를 정하다
4. 점 샘플링(x,y곡선 내의 선 세그먼트에서 )
5. 신품을 사용하여 2단계부터 반복하십시오.x가치를 매기다

여기서의 동기는 임의 곡선 내에서 점을 균일하게 표본으로 추출하는 한 가지 방법이 먼저 전체 곡선을 가로질러 얇은 균일 높이 수평 슬라이스를 그리는 것이다.그런 다음, 이전 반복에서 x 위치의 곡선 아래나 아래로 떨어지는 슬라이스를 임의로 선택한 다음 슬라이스를 따라 x 위치를 랜덤하게 선택하여 곡선 내의 점을 표본으로 추출할 수 있다.알고리즘의 이전 반복에서 얻은 x 위치를 사용하여 장기적으로는 곡선 내 세그먼트의 길이에 비례하는 확률을 가진 슬라이스를 선택한다.이 알고리즘에서 가장 어려운 부분은 수평 슬라이스의 경계를 찾는 것인데, 여기에는 샘플링 대상 분포를 설명하는 함수를 뒤집는 것이 포함된다.이것은 특히 절편이 여러 개의 불연속 부품으로 구성될 수 있는 다중 모델 분포의 경우에 문제가 된다.이를 극복하기 위해 거절 샘플링의 형태를 사용하는 경우가 종종 있는데, 여기서 우리는 문제의 원하는 슬라이스를 포함하는 것으로 알려진 더 큰 슬라이스에서 샘플을 추출한 다음 원하는 슬라이스 외부에 있는 점을 폐기한다.이 알고리즘은 함수가 1에 통합되는지 여부에 관계없이 어떤 곡선 아래 면적에서 샘플링하는 데 사용할 수 있다.실제로 상수에 의한 함수의 스케일링은 샘플링된 x-포지션에 영향을 미치지 않는다.이는 확률밀도함수가 계산 통계에서 흔히 볼 수 있는 상수(즉, 정규화 상수를 알 수 없는)까지만 알고 있는 분포로부터 표본을 추출하는 데 알고리즘을 사용할 수 있다는 것을 의미한다.

실행

슬라이스 샘플링은 첫 번째 단계에서 이름을 얻는다. 보조 $변수{\displaystyle }$ Y ${\displaystyle$ Y$}$에서 샘플링하여 슬라이스를 정의한다$.$ 이 변수는${\displaystyle }$[ 0${\displaystyle ,}$ ${\displaystyle f}$( ${\displaystyle x}$) ${\displaystyle ]}$ ${\displaystyle [0,f(x)]$에서 샘플링된다$.$ $여기$서 f${\displaystyle }$( ${\displaystyle x}$) ${\displaystyf(x)$는 X의 확률밀도함수(PDF)이거나 최소한$$ PDF)와 비례한다.. $이것$은 F (${\displaystyle x}$) ${\displaystyle \ge }$ Y ${\displaystyle f(x)\geq Y}$의 한 조각을 정의한다$.$ 다시 말하면, 우리는 현재 확률밀도가 적어도 $Y{\displaystyle }$ ${\displaystyle Y}$인 X의 영역을 보고 있다$.$ 그러면 X의 다음 값은 이 슬라이스에서 균일하게 샘플링된다.$Y{\displaystyle }$ ${\displaystyle Y}$의 새로운 값이 샘플링된 다음 X 등으로 샘플링된다$$.이는 PDF에 따라 y 위치를 샘플링한 다음 포인트의 x 위치를 샘플링하는 것으로 시각화할 수 있으며, 따라서 Xs는 원하는 분포로부터 나온 것이다.$Y{\displaystyle }$ ${\displaystyle Y}$ 값은$$ 절차에 대한 유용성 외에 특별한 결과나 해석을 포함하지 않는다.

PDF와 PDF의 역수를 모두 사용할 수 있고 분포가 단수일 경우 슬라이스 찾기 및 샘플링이 간단하다.그렇지 않은 경우, 끝점이 슬라이스 외부에 있는 지역을 찾기 위해 발판 절차를 사용할 수 있다.그런 다음 거부 샘플링을 사용하여 슬라이스에서 샘플을 추출할 수 있다.이를 위한 다양한 절차가 닐에 의해 자세히 설명되어 있다.^[2]

균일하지 않은 분포로부터 난수를 생성하기 위해 이용 가능한 많은 방법과는 대조적으로, 이 접근방식에 의해 직접 생성된 난수변수는 연속적인 통계적 의존성을 나타낼 것이다.다음 표본을 그리기 위해 현재 표본에 대한 f(x) 값을 기준으로 슬라이스를 정의하기 때문이다.

다른 방법에 비해

슬라이스 샘플링은 마르코프 체인 방식으로, 깁스 샘플링 및 메트로폴리스와 같은 목적을 제공한다.메트로폴리스와 달리 후보 기능이나 후보 표준 편차를 수동으로 조정할 필요가 없다.

메트로폴리스가 스텝 사이즈에 민감하다는 것을 기억하라.스텝 크기가 너무 작을 경우 무작위 보행은 실내 장식을 느리게 한다.스텝 규모가 너무 크면 높은 거부율로 인한 비효율성이 크다.

Metropolitania와 대조적으로 슬라이스 샘플링은 밀도 함수의 국소 모양에 맞게 단계 크기를 자동으로 조정한다.구현은 깁스 샘플링이나 간단한 메트로폴리스 업데이트보다 훨씬 쉽고 효율적이다.

균일하지 않은 분포로부터 난수를 생성하기 위해 이용 가능한 많은 방법과는 대조적으로, 이 접근방식에 의해 직접 생성된 난수변수는 연속적인 통계적 의존성을 나타낼 것이다.즉, 모든 점이 같은 독립적 선택 가능성을 갖는 것은 아니다.다음 표본을 그리기 위해 현재 표본에 대한 f(x) 값을 기준으로 슬라이스를 정의하기 때문이다.그러나 생성된 샘플은 마크노비안(markovian)이므로 장기적으로 정확한 분포로 수렴할 것으로 예상된다.

슬라이스 샘플링은 샘플링할 분포를 평가할 수 있어야 한다.이 요구사항을 완화하는 한 가지 방법은 진정한 비평가 분포에 비례하는 평가 가능한 분포를 대체하는 것이다.

일변량 케이스

주어진 표본 x의 경우, y 값은 [0, f(x)]에서 선택된다. 이 값은 분포의 "슬라이스"를 정의한다(솔리드 수평선으로 표시).이 경우 분포 범위 밖의 영역으로 분리된 두 개의 슬라이스가 있다.

농도 f(x)로 랜덤 변수 X를 표본으로 추출하기 위해 보조 변수 Y를 도입하고 다음과 같이 반복한다.

• 표본 x에 따라 [0, f(x)] 구간에서 랜덤으로 y를 균일하게 선택한다.
• y를 지정하면 ${\displaystyle {\mathrm{f}}^{}}$- 1${\displaystyle {}^{}}$[ ${\displaystyle y}$ , + $+$ $displaystyle f^{-1}[y,+\fty )}$ 집합에서 x를 임의로 선택한다$.$
• x의 표본은 y 값을 무시하여 얻는다.

우리의 보조 변수 Y는 분포의 수평 "슬라이스"를 나타낸다.각 반복의 나머지 부분은 고려 대상 지역의 밀도를 나타내는 x 값을 슬라이스에서 샘플링하는 데 사용된다.

실제로 다모달 분포의 수평 슬라이스에서 추출하는 것은 어렵다.큰 샘플링 영역을 획득하고 그에 따라 분배 공간에서 큰 움직임을 보이는 것과 효율을 높이기 위해 샘플링 영역을 단순화하는 것 사이에는 긴장이 있다.이 과정을 단순화하기 위한 한 가지 방법은 지역적 확장과 수축이다.

• 첫째, 폭 매개변수 w는 주어진 'x 값을 포함하는 영역을 정의하는 데 사용된다. 이 영역의 각 끝점은 지정된 슬라이스 외부에 있는지 확인하기 위해 테스트된다. 그렇지 않은 경우, 영역은 w에 의해 적절한 방향으로 확장되며, 끝은 두 끝점이 슬라이스 외부에 위치할 때까지 확장된다.
• 후보 표본은 이 지역 내에서 균일하게 선택된다.후보 샘플이 슬라이스 안에 있으면 새 샘플로 인정된다.만약 그것이 조각 밖에 있다면, 후보 지점은 지역의 새로운 경계선이 된다.새로운 후보 샘플은 균일하게 채취된다.후보 샘플이 슬라이스 내에 있을 때까지 프로세스가 반복된다.(시각적 예는 도표 참조).

일련의 슬라이스가 주어진 샘플 찾기(슬라이스는 여기서 파란색 선으로 표시되며 f(x)의 이전 그래프에서 단색 선 슬라이스에 해당함). w 폭 매개변수 w가 설정된다. b) w의 넓이 영역은 주어진 점 x$$을 중심으로 $식별$된다(\$displaystyle$ x_{$0$ 두 끝점이 모두 바깥에 있을 때까지 w로 영역이 확장된다.고려된 슬라이스 중에서. $d{\displaystyle {}_{}}$) ${\displaystyle {x\mathrm{}}_{}}$1 {\$displaystyle x_{$1}{1}를 지역에서 균일하게 선택한다$$.e) $x{\displaystyle {}_{}}$ ${\$}는 고려된 슬라이스 외부에 있으므로$$, 영역의 왼쪽 경계를 $x{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$f) 또 다른 균일한 $샘플{\displaystyle }$ x$${\$displaystyle$ x$}$는 고려된 슬라이스 내에 있으므로 샘플로 받아들여진다.

→

조각군-기브스 표본 추출

Gibbs sampler에서는 모든 완전 조건 분포로부터 효율적으로 도출할 필요가 있다.완전 조건 밀도에서 샘플링이 쉽지 않은 경우, 해당 변수에서 샘플링하기 위해 Gibbs 내에서 슬라이스 샘플링의 단일 반복 또는 Metropolitan-Hastings 알고리즘을 사용할 수 있다.전체 조건 밀도가 로그 콘케이브일 경우, 보다 효율적인 대안은 적응 거부 샘플링(ARS) 방법을 적용하는 것이다.^[4][5]ARS 기법을 적용할 수 없을 때(전체 조건이 로그 콘카베가 아니기 때문에), 적응 거부 Metropolitude 샘플링 알고리즘이 채택되는 경우가 많다.^[6][7]

다변량법

각 변수를 독립적으로 처리

단일 변수 슬라이스 샘플링은 Gibbs 샘플링에서처럼 각 변수를 차례대로 반복적으로 샘플링하여 다변량 사례에서 사용할 수 있다.그렇게 하려면 각 구성 요소 x ${\displaystyle i_{}}$ ${\$에 대해 $p{\displaystyle }$( x ${\displaystyle {}_{}}$ ${\displaystyle x{}_{}{}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$.${\displaystyle }$. . . $){\displaystyle p(x_{i} x_{0})$에 비례하는 함수를$$ 계산할 수 있어야 한다.$x_{n}}}$.

무작위 보행 동작을 방지하기 위해 과완화 방법을 사용하여 각 변수를 차례대로 업데이트할 수 있다.^{[citation needed]}과완화는 Gibbs에서 행해진 것과 같이 분포로부터 새로운 독립적 값을 선택하는 것과는 반대로, 모드 반대편의 새로운 값을 현재 값에서 선택한다.

초직각 슬라이스 샘플링

이 방법은 다변량 사례에 단변량 알고리즘을 적용하여, 원문에서 사용하는 1차원 w영역에 대해 초직각을 대체한다.고직각 H는 슬라이스 위에 임의의 위치로 초기화된다.그 후 H는 그것의 포인트가 거부됨에 따라 축소된다.

반사 슬라이스 샘플링

반사 슬라이스 샘플링은 경계에 도달한 후 샘플링 방향을 슬라이스를 향해 안쪽으로 "반사"함으로써 분배 f(x)의 연속 후보 샘플이 슬라이스 범위 내에 유지되는 무작위 보행 동작을 억제하는 기법이다.

반사 샘플링의 이 그래픽 표현에서 형상은 샘플링 슬라이스의 경계를 나타낸다.점들은 샘플링 워크의 시작점과 정지점을 나타낸다.샘플이 슬라이스 한계에 도달하면 샘플링 방향이 다시 슬라이스로 "반사"된다.

예

단일 변수 예를 고려하십시오.Suppose our true distribution is a normal distribution with mean 0 and standard deviation 3, ${\displaystyle g(x)\sim N(0,3^{2})}$. So: ${\displaystyle f(x)={\frac {1}{\sqrt {2\pi \cdot 3^{2}}}}\ e^{-{\frac {(x-0)^{2}}{2\cdot 3^{2}}$$\}\}\}\}.$ 분포의 최고점은 $분명히{\displaystyle }$x = ${\displaystyle 0}${\$displaystyle$ x$=0}$이며$,$ $이때{\displaystyle }$ f${\displaystyle (x}$ ${\displaystyle )}$는 0${\displaystyle .1330}$ ${\displaystyle$f$(x)\약 0.1330}$이다$.$

1. 우리는 먼저 우리의 슬라이스를 정의하기 위해 f(x)의 범위에서 균일한 무작위 값 y를 그린다. f(x)의 범위는 0에서 ~0.1330까지이므로 이 두 극단 사이의 값은 모두 충분하다.y = 0.1을 사용한다고 가정합시다.문제는 y 값이 0.1보다 큰 점을 어떻게 표본으로 추출하느냐가 된다.
2. 다음으로, 우리는 우리의 고려 영역을 확장하기 위해 사용할 폭 매개변수를 설정한다.이 값은 임의의 값이다.w = 2라고 가정합시다.
3. 다음으로 x에 대한 초기값이 필요하다. f(x) > 0.1(우리의 y 매개변수)을 만족하는 f(x) 영역 내의 균일한 분포로부터 x를 끌어낸다.x = 2라고 가정합시다.이것은 f(2) = ~0.1065 > 0.1이기 때문에 효과가 있다.^[8]
4. x = 2 및 w = 2이기 때문에 현재 관심 영역은 (1, 3)으로 제한된다.
5. 이제, 이 영역의 각 끝점이 주어진 슬라이스 밖에 있는지 확인하기 위해 테스트된다.우리의 오른쪽 경계는 우리의 슬라이스(f (3) = ~0.0807 < 0.1) 밖에 있지만, 왼쪽 값은 (f(1) = ~0.1258 > 0.1)가 아니다.우리는 slice의 한도를 지나 확장될 때까지 w를 거기에 더함으로써 왼쪽 경계를 확장한다.이 과정을 거쳐 우리 관심 영역의 새로운 한계는 (-3, 3)이다.
6. 다음으로 (-3, 3) 내에서 균일한 표본을 채취한다.이 표본이 x = -2.9를 산출한다고 가정합시다.이 샘플은 우리의 관심 영역 내에 있지만, 우리의 슬라이스 (f(2.9) = ~0.08334 < 0.1) 내에 있지 않기 때문에, 우리는 우리의 관심 영역의 왼쪽 경계를 이 지점으로 수정한다.이제 (-2.9, 3)에서 균일한 샘플을 채취한다.이번에 우리의 샘플이 x = 1을 산출한다고 가정하자. 이는 우리의 슬라이스 샘플링에 의해 승인된 샘플 출력이다.만약 우리의 새로운 x가 우리의 조각 안에 없다면, 우리는 유효한 x가 한계 내에 있을 때까지 수축/재샘플링 과정을 계속할 것이다.

분포의 정점에 관심이 있다면, 새로운 점이 원래의 점보다 높은 f(x)에 해당하기 때문에 이 과정을 계속 반복할 수 있다.

다른 예

To sample from the normal distribution ${\displaystyle N(0,1)}$ we first choose an initial x—say 0. After each sample of x we choose y uniformly at random from ${\displaystyle (0,e^{-x^{2}/2}/{\sqrt {2\pi }}]}$, which is bounded the pdf of ${\displaystyle N(0,1)}$.After each y sample we choose x uniformly at random from ${\displaystyle [-\alpha ,\alpha ]}$ where ${\displaystyle \alpha ={\sqrt {-2\ln(y{\sqrt {2\pi }})}}}$. This is the slice where ${\displaystyle f(x)>y}$.

Macsyma 언어로 구현된 내용은 다음과 같다.

slice(x) :=block([y, alph), y:sni(expx^2 / 2.0) / sqrt(2.0 * dfloat(%pi)), alpha:sqrt2.0 * ln(y * sqrt(2.0 * dfloat(%pi)), x:signum * rand(lossignum );

참고 항목

• 마르코프 체인 몬테카를로

참조

외부 링크

• http://www.probability.ca/jeff/java/slice.html