살리논
Salinon살리논(그리스어로 '소금-셀라'라는 뜻)은 4개의 반원형으로 이루어진 기하학적 형상이다. 아르키메데스에게 귀속된 작품인 레마스의 책에 처음 소개되었다.[1]
건설
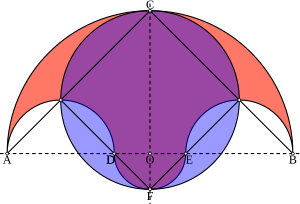
O를 데카르트 비행기의 기원이 되게 하라. A, D, E, B를 한 줄에 4점, 그 순서대로 O를 이등분하여 AB로 한다. AD = EB로 하자. 반원은 AB선 위에 지름 AB, AD, EB로 그리고 또 다른 반원은 지름 DE로 그려진다. 살리논은 이 네 개의 반원으로 둘러싸인 형상이다.[2]
특성.
면적
아르키메데스는 유클리드 원소의 제2권 제10호를 적용하여 레마스의 저서에서 살리논을 소개했다. 아르키메데스는 "모든 반원[]의 원형으로 경계를 이룬 인물의 면적이 지름으로 CF 상의 원의 면적에 해당한다"[3]고 지적했다.
즉, 살리논의 면적은 다음과 같다.[4]
아르벨로스
D점과 E점이 O와 수렴할 경우, 그것은 아르키메데스의 또 다른 창조물 중 하나인 아르벨로를 형성하고, Y축을 따라 대칭을 이루게 된다.[3]
참고 항목
참조
- ^ Heath, T. L. (1897). "On the Salinon of Archimedes". The Journal of Philology. 25 (50): 161–163.
- ^ Nelsen, Roger B. (April 2002). "Proof without words: The area of a salinon". Mathematics Magazine. 75 (2): 130. doi:10.2307/3219147. JSTOR 3219147.
- ^ a b Bogomolny, Alexander. "Salinon: From Archimedes' Book of Lemmas". Cut-the-knot. Retrieved 2008-04-15.
- ^ Weisstein, Eric W. "Salinon". MathWorld.
외부 링크
- 라르벨로스 Partie 2 by Hamza Khelif, CNRS www.images.math.cnrs.fr