무작위 결정 규칙

통계결정론에서 무작위결정규칙 또는 혼합결정규칙은 확률과 결정론적 의사결정규칙을 연관짓는 결정규칙이다.유한 의사결정 문제에서 무작위 의사결정 규칙은 비임의 의사결정 규칙의 위험 지점의 볼록한 껍질인 위험 집합을 정의한다.

랜덤화된 베이즈 규칙에 대한 비랜덤화 대안은 항상 존재하기 때문에, 베이지안 통계에는 랜덤화가 필요하지 않다. 그러나 빈도주의 통계 이론은 때때로 최소값과 같은 최적 조건을 충족하기 위해 랜덤화 규칙을 사용해야 하며, 특히 이산 프로바비에 대한 신뢰 구간과 가설 테스트를 도출할 때 가장 두드러진다.리티 분포

랜덤화 결정 규칙을 이용한 통계 테스트를 랜덤화 테스트라고 합니다.

정의와 해석

$p_{1},p_{2},...,p_{h}$ ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ { ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ 、 ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ 2 ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ . . , ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ h $}$ { $displaystyle$ { D } = \ { $d$ _ { d _ { $}$ , d _ { $h$ } 、 $d_$ { displaystyle p ${\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}$ _ { $1$ } 、 . $p_{1},p_{2},...,p_{h}$ 、 $p$ } { $h$ } $p_{1},p_{2},...,p_{h}$ 、 { $displaystyle$ p _ { discal p _ { D } } } 。d $\sum _{i=1}^{h}p_{i}d_{i}$ i $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ $\sum _{i=1}^{h}p_{i}d_{i}$ $\sum _{i=1}^{h}p_{i}d_{i}$ p i $\sum _{i=1}^{h}p_{i}d_{i}$ { $displaystyle \sum$ _ { i $\sum _{i=1}^{h}p_{i}d_{i}$ = { $i$ } p _ { $h$ $R(\theta ,d^{*})$ $d$ _ { $\sum _{i=1}^{h}p_{i}d_{i}$ $i$ } its $\sum _{i=1}^{h}p_{i}d_{i}$ its its $R(\theta ,d^{*})$ its its $R(\theta ,d^{*})$ its its $its$ R ( \ $theta$ , $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ $^$ { * $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ } ) $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ = $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ p $\sum _{i=1}^{h}p_{i}R(\theta ,d_{i})$ ( \ $sum$ stylash , $display$ $style$ ) $_$ 1 .이 규칙은 d1 $d_{1},...,d_{h}\in {\mathcal {D}}$ . $d_{1},...,d_{h}\in {\mathcal {D}}$ . $d_{1},...,d_{h}\in {\mathcal {D}}$ . , $d_{1},...,d_{h}\in {\mathcal {D}}$ h $d_{1},...,d_{h}\in {\mathcal {D}}$ D { $displaystyle d_{1}$ , . . . $mathcal$ { $D}$ \ $in$ \ mathcal { D } \ $d_{h$ } $d_{1},...,d_{h}\in {\mathcal {D}}$ $d_{1},...,d_{h}\in {\mathcal {D}}$ $p_{1},...p_{h}$ , $p_{1},...p_{h}$ . . $p_{1},...p_{h}$ . $p_{1},...p_{h}$ \ $displaystyle p_{$ } ... selected rules $p_{1},...p_{h}$ rules rules rules rules rules rules rules rules rules rules rules rules rules d d d with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with with $p_{1},...p_{h}$ with with with $p_{h}}$ 입니다 $p_{1},...p_{h}$ .^[2]

또는 무작위 의사결정 규칙은 표본 공간의 각 구성원에 대해 작용 ${\mathcal {A}}$ 의 ${\mathcal {A}}$ $요소$ 에 직접 확률을 할당할 수 있다 $.$ 좀 더 형식적으로 d $d^{*}(x,A)$ ( $d^{*}(x,A)$ , $d^{*}(x,A)$ A ) \ $displaystyle$ d $^{*} ($ x , $d^{*}(x,A)$ A )는 $d^{*}(x,A)$ $a\in {\mathcal {A}}$ $a\in {\mathcal {A}}$ \ $displaystyle a$ \ $in$ \ mathcal { $A$ } 가 선택되었을 확률을 나타냅니다.이 접근법에서 손실함수는 직접 다음과 같이 정의됩니다 $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ A $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ ( $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ , $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ ) $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ ( $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ , $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ ) $\int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA$ A \ $display$ style \ $int$ _ { $A$ \ $in$ \ $mathcal$ { $A$ } d^ { * （ $x$ , $A$ ) $L$ ( \ $theta , A$ ) $DA$ ^[3]

따라서 무작위 의사결정 규칙의 도입은 통계학자가 자신의 결정을 선택할 수 있는 더 큰 의사결정 공간을 만든다.비랜덤화 의사결정 규칙은 하나의 의사결정 또는 행동이 확률 1을 갖는 무작위 의사결정 규칙의 특수한 경우이므로, 원래의 ${\mathcal {D}}$ 공간 ${\mathcal {D}}$ D $(\$ $displaystyle\mathcal {D})$ 는 $\mathcal D$ 새로운 의사결정 ${\mathcal {D}}^{*}$ D $(\displaystyle\mathcal {D$ ^[4]의 적절한 부분 집합이다.

무작위 의사결정 규칙 선택

빈 원으로 표시된 위험 집합의 극한점은 랜덤화되지 않은 의사결정 규칙에 해당하며 굵은 선은 허용 가능한 의사결정 규칙을 나타낸다.

랜덤화되지 않은 의사결정 규칙과 마찬가지로 랜덤화 의사결정 규칙은 수용성, 최소성 및 베이스와 같은 유리한 속성을 충족할 수 있다.이는 유한한 의사결정 문제, 즉 매개변수 공간이 k $\displaystyle$ k $k$ 의 $k$ 유한 세트인 문제의 경우에 설명되어야 한다.이후 S $(\$ 로 ${\mathcal {S}}$ 되는 리스크세트는 모든 벡터의 집합입니다.각 엔트리는 특정 파라미터의 랜덤화 결정 규칙과 관련된 리스크 함수의 값입니다.이 값에는 $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ 모든 형식의 벡터( $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " ( $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " 1, $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " , $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ d " ) $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ ) , $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ . $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ . $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ ( " $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ k , $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ ) $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ , $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " ) ) ) , " " " " $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " $(R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}$ " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " $§$ $R(\theta$ _ ${k}, d^{*}), d^{*}\in {mathcal {D$ 랜덤화된 의사결정 규칙의 정의에 따라 $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ 집합은 $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ 의 $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ 볼록한 선체( $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ ( 1 1, $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ ) $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ , . $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ R ( $θ$ $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ ) , $、$ $(R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}$ { $tyledisplay$ \ $tyle$ } ) 。 $R(\theta$ _ ${k$ }, $d),d\in {mathcal {D$ ^[5]

파라미터 공간에 1 $(\$ $displaystyle$ $\theta$ _ ${1})$ 과 $\theta _{1}$ $(\$ _ ${2$ 의 두 요소만 있는 경우, 이는 $\mathbb {R} ^{2}$ 2(\ $displaystyle \mathbb {R$ 의 서브셋을 구성하므로 $R_{1}$ R $R_{1}$ (\ $displaystyle R_1})$ 과 $R_{1}$ R dis 2 $($ )에 대해 그릴 수 있습니다.§^[6] $($ _ ${1})$ 및 $\theta _{1}$ § $($ _ ${2})$ 에 $\theta _{2}$ 해당하는 $playstyle R_{2}.$ 오른쪽에 예가 나와 있습니다.

수용성

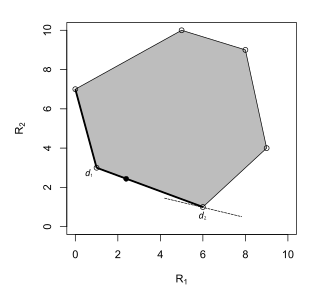
허용 가능한 의사결정 규칙은 다른 의사결정 규칙에 의해 지배되지 않는 규칙이다. 즉, 모든 매개변수에 대해 위험과 같거나 낮은 위험을 가지며 일부 매개변수에 대해서는 위험보다 엄격하게 낮은 의사결정 규칙이 없다.유한 결정 문제에서 허용 결정 규칙의 위험 지점은 다른 모든 위험 지점보다 낮은 x-변환율 또는 y-변환율을 갖거나 $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $보다 형식적으로 {$ ( $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ 1, $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ ) : $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ a $(a,b)$ , $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ 2 $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $(a,b)$ $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ $\{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)$ 형태의 $(a,b)$ 위험 지점을 갖는 규칙 $(a,b)$ 이다. $\{(R_{1},R_{2}):$ $R_{1}\leq$ a, $R_{2}\leq$ b $\}\cap {mathcal {S}=(a,b$ 따라서 위험 집합의 하위 경계 왼쪽은 허용되는 결정 ^[6]^[7]규칙 집합이다.

미니맥스

minimax Bayes ${\mathcal {D}}^{*}$ 은 D의 모든 의사결정 규칙 중 Supremum $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ sup $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ （ $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ 、 d $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ sometimes $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ ） \ $displaystyle$ \ $sup$ _ { \ $theta$ \ $in$ \ $Theta } R$ ( \ $theta$ , $d^$ { * } ){ $displaystyle$ \ $mathcal$ { $D$ }^{ * } ${\mathcal {D}}^{*}$ }}}}}}}}의 $\sup _{\theta \in \Theta }R(\theta ,d^{*})$ 규칙을 최소화하는 경우가 있습니다.존중이다.^[1]

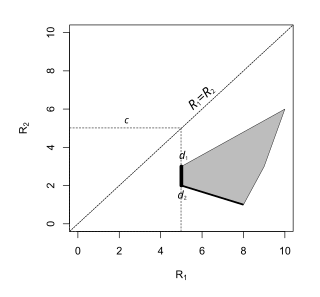
2개의 가능한 파라미터가 있는 유한한 결정문제의 경우 $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ 미니맥스규칙은 $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ ( c ) $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ { ( $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ , $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ R $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ ) : $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ R $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ , 0 $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ R $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ {\ c $Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}$ ( \ $displaystyle$ Q ( c ) = \ { ( $R$ _ { $1$ , R _ $2$ } \ 0 $q$ R _ 1 $le$ :S $(\$ 에 ${\mathcal {S}}$ ${\mathcal {S}}$ 가장 작은 정사각형에 대한 c $(\displaystyle$ c $)$ $c$ 은 $c$ 최소 위험이며 위험 집합에서 대응하는 하나 이상의 점이 최소 규칙입니다.

위험 집합이 $R_{1}=R_{2}$ $R_{1}=R_{2}$ $=$ ({ $displaystyle R_{1$ }= $R_{2$ 와 교차하는 경우, 라인 상에 허용되는 결정 규칙은 미니맥스입니다. $R_{2}>R_{1}$ 2 $R_{2}>R_{1}$ > $R_{2}>R_{1}$ $R_{2}>R_{1}$ (\ $style R_{$ 2} > $R_{1}$ ) $R_{1}>R_{2}$ R $R_{1}>R_{2}$ > $R_{1}>R_{2}$ 2 (\ $displaystyle R_{1}$ > $R_{2}})$ 이 $R_{1}>R_{2}$ 리스크 세트의 모든 포인트에 대해 유지되고 있는 $R_{2}>R_{1}$ 미니맥스 규칙은 극단점(즉, 랜덤하지 않은 결정 규칙) 또는 2개의 극단점을 연결하는 회선(랜덤화되지 않은 결정 규칙)^[9]^[6]이 될 수 있습니다.

minimax 규칙은 랜덤화된 결정 $(1-p)d_{1}+pd_{2}$ 규칙( $(1-p)d_{1}+pd_{2}$ - $(1-p)d_{1}+pd_{2}$ p ) $(1-p)d_{1}+pd_{2}$ + $(1-p)d_{1}+pd_{2}$ $(1-p)d_{1}+pd_{2}$ 2 { $displaystyle (1-p) d_{1}$ + $pd_{2$ 입니다.
minimax 규칙은 $({$ 입니다.
미니맥스 규칙은 $(1-p)d_{1}+pd_{2}$ ( $(1-p)d_{1}+pd_{2}$ - p ) $(1-p)d_{1}+pd_{2}$ + $(1-p)d_{1}+pd_{2}$ d $(1-p)d_{1}+pd_{2}$ 2 { { $displaystyle$ ( $(1-p)d_{1}+pd_{2}$ 1 - p ) $d$ _ { $1$ $0\leq p\leq 1$ + $pd$ _ {2} $(1-p)d_{1}+pd_{2}$ } , $0\leq p\leq 1$ 1 $0\leq p\leq 1$ { $displaystyle$ 0 $\leq p\leq$ 1 $0\leq p\leq 1$ 형식의 규칙입니다.

베이즈

랜덤화된 Bayes 규칙은 모든 의사결정 규칙 중 최소 Bayes $r(\pi ,d^{*})$ r ( " $r(\pi ,d^{*})$ , $r(\pi ,d^{*})$ " $){$ r ( \ $pi$ , $d^$ { * } )를 $r(\pi ,d^{*})$ 갖는 규칙입니다.파라미터 공간에 2개의 요소가 있는 특수한 경우, 행 $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ 1 $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ + ( $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ 1 - $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ 1 ) $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ $\pi _{1}R_{1}+(1-\pi _{1})R_{2}=c$ $=$ c \ $display style$ \ $pi$ _ { $1}R_{1}+(1-\pi$ _ ${1})$ $R_{2}=c$ 여기서 $\pi _{1}$ $\pi _{1}$ 1 $(\displaystyle$ \ $pi _{$ 1}) 및 $\theta _{2}$ $\pi _{2}$ 2 $(\$ $theta$ _ ${2})$ 는 $\pi _{2}$ $\theta _{2}$ 각각 $\theta _{1}$ 1(\ $displaystyle$ $\$ $theta$ $\theta _{1}$ _ $c$ $2$ })의 $\theta _{1}$ 이전 확률을 나타냅니다 $).$ 따라서 의사결정 문제에 대한 Bayes의 최소 위험은 선이 위험 ^[10]^[11]세트에 닿도록 최소 $c$ \ $displaystyle c이다$ 이 선은 위험 집합의 한 극단점(즉, 비랜덤화 의사결정 규칙)에만 닿거나 위험 집합의 전체 측면(즉, 두 가지를 결합한 두 가지 비랜덤 의사결정 규칙 및 무작위 의사결정 규칙)과 겹칠 수 있다.이는 다음 세 가지 상황에서 확인할 수 있습니다.

베이즈 규칙은 ( $(1-p)d_{1}+pd_{2}$ - $(1-p)d_{1}+pd_{2}$ $(1-p)d_{1}+pd_{2}$ $(1-p)d_{1}+pd_{2}$ + $(1-p)d_{1}+pd_{2}$ $(1-p)d_{1}+pd_{2}$ ({ $displaystyle (1-p) d_{1}$ + $pd_{2$ $0\leq p\leq 1$ $0\leq p\leq 1$ $0\leq p\leq 1$ $0\leq p\leq 1$ $0\leq p\leq 1$ $({$ $displaystyle$ 0 $\leq$ p $\leq$ 1 $0\leq p\leq 1$ $(1-p)d_{1}+pd_{2}$ 형식의 결정 규칙 세트입니다.
Bayes 규칙은 $(\$ 입니다.
Bayes 규칙은 $({$ 입니다.

서로 다른 선행으로 인해 다른 기울기가 발생하므로, 이전의 일부 규칙과 관련하여 베이즈인 모든 규칙 집합은 허용 가능한 ^[12]규칙 집합과 동일하다.

랜덤화되지 않은 Bayes 규칙이 존재하지 않고 랜덤화 된 Bayes 규칙이 존재하는 상황은 없습니다.랜덤화된 베이즈 규칙의 존재는 랜덤화되지 않은 베이즈 규칙의 존재를 암시한다.이는 파라미터 공간이 무한하고 Bayes 리스크가 무한하며 Bayes 리스크가 최소가 ^[3]^[12]될 수 있는지 여부에 관계없이 일반적인 경우에도 마찬가지입니다.이는 통계학자가 통계적 ^[4]의사결정에 도달하기 위해 무작위화를 이용할 필요가 없다는 직관적 개념을 뒷받침한다.

실제로

랜덤화된 베이즈 규칙은 항상 랜덤화되지 않은 대안을 가지고 있기 때문에, 베이지안 통계에서는 불필요하다.그러나 빈도주의 통계에서 랜덤화 규칙은 이론적으로 특정 ^[13]상황에서 필요하며, 처음 발명되었을 때 실제로 유용한 것으로 생각되었다.Egon Pearson은 그들이 '강력한 ^[14]반대에 부딪히지 않을 것'이라고 예측했다.그러나 요즘은 실제로 ^[14]^[15]이를 시행하는 통계학자는 거의 없다.

랜덤화 테스트

랜덤화 검정은 치환 ^[16]검정과 혼동해서는 안 됩니다.

우도비 검정의 일반적인 공식에서는 우도비 $\Lambda$ \ $displaystyle\Lambda}$ 가 $\Lambda$ $상수$ K(\ $displaystyle$ K $K$ 보다 작을 때마다 귀무 가설이 기각되고 그렇지 않을 경우 받아들여진다.그러나 $\Lambda$ (\ $displaystyle \Lambda)$ 가 $\Lambda$ 귀무 가설에서 이산형인 경우 $\Lambda =K$ = K(\displaystyle \ $Lambda = K)$ 가 $\Lambda =K$ 가능한 경우 문제가 발생할 수 있습니다.

해결책은 테스트 함수 $\phi (x)$ ( $\phi (x)$ $)\displaystyle \phi (x$ 를 정의하는 것입니다.이 값은 귀무 가설이 ^[17]^[18]받아들여질 확률입니다.

$\phi (x)=\left\{\text{array}{l}1&{\text{if}}\Lambda >K\p(x)&{\text{if}}}\Lambda =K\0&{\text{array}}\오른쪽.$

이는 $\Lambda =k$ (\ $displaystyle$ \ $Lambda =k$ )일 $p(x)$ $\Lambda =k$ 때마다 헤드가 반환되고 헤드가 ^[15]나타나면 귀무 가설을 거부할 $p(x)$ p $(x)$ 로 편향된 동전을 던지는 것으로 해석된다.

Neyman-Pearson 준칙의 일반화된 형태에는 이 테스트가 동일한 $\alpha$ 수준α $(\displaystyle$ \alpha $\alpha$ 의 모든 테스트 중에서 최대 힘을 가지며, 그러한 테스트는 $\alpha$ 수준α $(\displaystyle$ \alpha $\alpha$ 에 대해 존재해야 하며, 테스트는 ^[19]정상적인 상황에서 고유하다고 명시되어 있다.

는 내부 분포는 베르누이 확률 p{p\displaystyle}과 한 예로서, 그리고 우리는 대립 가설 p대리자에 대한 공 가설 p≤ λ{p\leq \lambda\displaystyle}를 테스트해 보고 싶;λ{\displaystyle p>, \lambda} k{\displaystyl을 선택하는 것이 자연적인 고려해 보라.ek} P $P({\hat {p}}>k|H_{0})=\alpha$ ( $P({\hat {p}}>k|H_{0})=\alpha$ > $P({\hat {p}}>k|H_{0})=\alpha$ $P({\hat {p}}>k|H_{0})=\alpha$ ) $P({\hat {p}}>k|H_{0})=\alpha$ (\ $displaystyle$ P $({\hat$ {p $}}$ > $k H_{0$ }) = \alpha $P({\hat {p}}>k|H_{0})=\alpha$ } 이며 ${\hat {p}}>k$ ${\hat {p}}$ p ${\hat {p}}>k$ $^$ {\ $displaystyle {p}}} > k$ } ${\hat {p}}>k$ 늘을 거부합니다. ${\hat {p}}$ 서 p ^ {\ $displaystyle {p}$ 은 ${\hat {p}}$ 테스트 통계 정보입니다.그러나 p ${\hat {p}}=k$ ^ ${\hat {p}}=k$ ${\hat {p}}=k$ \ $displaystyle$ \ $hat {$ p} $=$ 인 경우를 ${\hat {p}}=k$ 하여 테스트 함수를 정의합니다.

$\phi (x)=\left\{\hat{array}{l}1&{\text{if}}{\hat {p}}}=k\0&{\text{if}}{\hat {p}}}{\hat {p}}}{\text{\hat {array}}}\right}\right}.$

$여기서$ P $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ ( $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ $>$ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ 0 ) $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ + $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ P ( $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ ^ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ 0 ) $α$ ( \ $displaystyle$ P ( { \ $hat$ { $p$ } } ) + \ $gamma$ P ( { \ $hat$ { p } $=$ k $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ H $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ _ 0 ） = $alpha$ $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ 로 $P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha$ 됩니다.

랜덤화된 신뢰 구간

신뢰 구간의 구성에서도 유사한 문제가 발생합니다.예를 들어, 이항 분포의 이산적 특성 때문에 Clopper-Pearson 구간은 항상 보수적입니다.다른 방법으로는 다음 방정식을 ^[14]풀어서 U\ $displaystyle$ $U$ $\$ $displaystyle$ L $\$ displaystyle U $\$ displaystyle L $\$ 의 $U$ $L$ 신뢰 $U$ 과 하한을 구하는 방법이 있습니다.

$\displaystyle \left\{\begin{array}{l}Pr({\hat {p}})+\gamma P({\hat {p}}=k p=U)&=\alpha /2\Pr({\hat {p}})&gamma P({\hat {\})=L)}$

$\gamma$ 서 $"\displaystyle\$ display $"$ 는 $\gamma$ (0, 1)의 균일한 랜덤 변수입니다.

「」를 참조해 주세요.

각주

^ ^a ^b Young and Smith, 페이지 11
^ Bickel and Doksum, 28페이지
^ ^a ^b 파르미지아니, 페이지 132
^ ^a ^b 디그루트, 페이지 128-129
^ Bickel and Doksum, 페이지 29
^ ^a ^b ^c Young and Smith, 페이지 12
^ Bickel and Doksum, 32페이지
^ Bikkel and Doksum, 페이지 30
^ 영과 스미스, 페이지 14-16
^ Young and Smith, 13페이지
^ Bickel and Doksum, 29~30페이지
^ ^a ^b Bickel and Doksum, 페이지 31
^ 로버트, 페이지 66
^ ^a ^b ^c 아그레스티와 고타드, 페이지 367
^ ^a ^b Bickel and Doksum, 224페이지
^ Onghena, Patrick (2017-10-30), Berger, Vance W. (ed.), "Randomization Tests or Permutation Tests? A Historical and Terminological Clarification", Randomization, Masking, and Allocation Concealment (1 ed.), Boca Raton, FL: Chapman and Hall/CRC, pp. 209–228, doi:10.1201/9781315305110-14, ISBN 978-1-315-30511-0, retrieved 2021-10-08
^ Young and Smith, 페이지 68
^ 로버트, 페이지 243
^ Young and Smith, 페이지 68

참고 문헌

Agresti, Alan; Gottard, Anna (2005). "Comment: Randomized Confidence Intervals and the Mid-P Approach" (PDF). Statistical Science. 5 (4): 367–371. doi:10.1214/088342305000000403.
Bickel, Peter J.; Doksum, Kjell A. (2001). Mathematical statistics : basic ideas and selected topics (2nd ed.). Upper Saddle River, NJ: Prentice-Hall. ISBN 978-0138503635.
DeGroot, Morris H. (2004). Optimal statistical decisions. Hoboken, N.J: Wiley-Interscience. ISBN 978-0471680291.
Parmigiani, Giovanni; Inoue, Lurdes Y T (2009). Decision theory : principles and approaches. Chichester, West Sussex: John Wiley and Sons. ISBN 9780470746684.
Robert, Christian P (2007). The Bayesian choice : from decision-theoretic foundations to computational implementation. New York: Springer. ISBN 9780387715988.
Young, G.A.; Smith, R.L. (2005). Essentials of Statistical Inference. Cambridge: Cambridge University Press. ISBN 9780521548663.

[ys11-1] Young and Smith, 페이지 11

[2] Bickel and Doksum, 28페이지

[parm-3] 파르미지아니, 페이지 132

[groot-4] 디그루트, 페이지 128-129

[bd29-5] Bickel and Doksum, 페이지 29

[ys12-6] Young and Smith, 페이지 12

[7] Bickel and Doksum, 32페이지

[bd30-8] Bikkel and Doksum, 페이지 30

[9] 영과 스미스, 페이지 14-16

[10] Young and Smith, 13페이지

[11] Bickel and Doksum, 29~30페이지

[bd31-12] Bickel and Doksum, 페이지 31

[13] 로버트, 페이지 66

[ag-14] 아그레스티와 고타드, 페이지 367

[bd224-15] Bickel and Doksum, 224페이지

[16] Onghena, Patrick (2017-10-30), Berger, Vance W. (ed.), "Randomization Tests or Permutation Tests? A Historical and Terminological Clarification", Randomization, Masking, and Allocation Concealment (1 ed.), Boca Raton, FL: Chapman and Hall/CRC, pp. 209–228, doi:10.1201/9781315305110-14, ISBN 978-1-315-30511-0, retrieved 2021-10-08

[17] Young and Smith, 페이지 68

[18] 로버트, 페이지 243

[19] Young and Smith, 페이지 68

[2]

[3]

[4]

[5]

[6]

[7]

[1]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

Search

무작위 결정 규칙

네임스페이스

더

목차

정의와 해석

무작위 의사결정 규칙 선택

수용성

미니맥스

베이즈

실제로

랜덤화 테스트

랜덤화된 신뢰 구간

「」를 참조해 주세요.

각주

참고 문헌

Search

무작위 결정 규칙

정의와 해석

무작위 의사결정 규칙 선택

수용성

미니맥스

베이즈

실제로

랜덤화 테스트

랜덤화된 신뢰 구간

「 」를 참조해 주세요.

각주

참고 문헌

「」를 참조해 주세요.