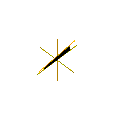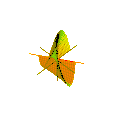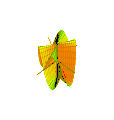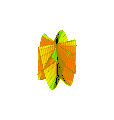플뤼커 코노이드

기하학에서 플뤼커의 코노이드(Conoid)는 독일의 수학자 율리우스 플뤼커(Julius Plucker)의 이름을 딴 지배된 표면이다.원뿔형 쐐기 또는 원통형 원통형이라고도 불리지만, 후자의 이름은 "실린드로이드"도 타원형 원통을 지칭할 수 있기 때문에 모호하다.

Plucker의 conoid는 다음 두 변수의 함수로 정의되는 표면이다.

${\displaystyle z={\frac {2xy}{x^{2}+y^{2}}.}$

이 함수는 기원에 본질적인 특이점을 가지고 있다.

우주에서 원통형 좌표를 사용하여 위의 함수를 파라메트릭 방정식으로 쓸 수 있다.

$[\displaystyle x=v\cos u,\display y=v\sin u,\display z=\sin 2u.}$

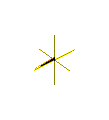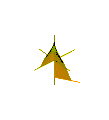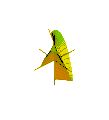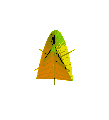
따라서 플뤼커의 코노이드(conoid)는 우측 코노이드로, 축의 세그먼트[-1, 1]를 따라 진동 운동(주기 2π)으로 z축에 대한 수평선을 회전시켜 얻을 수 있다(그림 4).

Plucker의 코노이드의 일반화는 파라메트릭 방정식에 의해 주어진다.

$\displaystyle x=v\cos u, \display y=v\sin u, \display z=\sin nu.}$

여기서 n은 표면의 접힘 수를 나타낸다.차이점은 z축을 따라 움직이는 진동 주기가 2㎛/n이라는 것이다(n = 3)

• 

  n=2가 붙은 플커 코노이드의 애니메이션

• 

  n=2가 있는 플커 코노이드

• 

  플커코노이드 n=3

• 

  n=2가 붙은 플커 코노이드의 애니메이션

• 

  n=3을 사용한 플럭커 코노이드의 애니메이션

• 

  플커코노이드 n=4

참고 항목

• 지배면
• 오른쪽 코노이드

참조

• A. Gray, E. Abbena, S. S. Salamon, Mathematica를 사용한 곡선과 표면의 현대적 차등 기하학, 3차 에드.플로리다 주 보카 라톤:CRC 프레스, 2006.[1] ( ISBN978-1-58488-448-4))
• 블라디미르 Y.Rovenskii, MAPLE을 사용한 곡선과 표면의 기하학 [2] (ISBN 978-0-8176-4074-3)

외부 링크

• Weisstein, Eric W. "Plücker's Conoid". MathWorld.