비명령 신호 흐름 그래프

오토마타 이론과 제어 이론, 수학, 이론 컴퓨터 과학 및 시스템 공학의 분과에서, 비전속 신호 흐름 그래프는 지시된 그래프의 가장자리를 링이나 연기에 매핑하여 상호 연결된 시스템과 상태 기계를 모델링하는^[1] 도구다.

단일 에지 중량은 복잡한 시스템의 일련의 충동 응답(오른쪽 그림 참조)^[2]을 나타낼 수 있고, 알파벳 문자는 유한 자동화의 입력 테이프를 떼어낼 수 있으며,^[3] 그래프는 정보 흐름이나 상태 전환을 나타낼 수 있다.

이러한 응용 프로그램들이 다양한 만큼, 그들은 많은 동일한 기초 이론을 공유한다.^[4][5]

정의

이 글은 독자들에게 혼란스럽거나 불명확할 수 있다.특히, 여기서 정의되는 것은 무엇인가? 기사에 대해 명확하게 설명할 수 있도록 도와주십시오. 토크 페이지에서 이에 대한 논의가 있을 수 있다.(2015년 9월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

n+1 변수 {x₀, x₁, ...,x_n}을(를) 포함하는 n 방정식을 고려하십시오.

${\displaystyle x_{i}=\sum _{j=0}^{na_{ij}x_{j}}\;\;1\leq i\leq n,}$

원소를_ij 링에 넣거나 R을 연마하는 것.자유 변수 x는₀ 소스 꼭지점 v에₀ 해당하므로 정의 방정식이 없다.각 방정식은 그림에서 볼 수 있는 방향 그래프 G=(V,E)의 조각에 해당한다.

에지 가중치는 E에서 R까지의 함수 f를 정의한다.마지막으로 출력 정점 v_m. 신호 흐름 그래프는 이 데이터 S = (G=(V,E), v₀,v_m${\displaystyle }$∈ ${\displaystyle \in }$, f : E → R)의 모음입니다.방정식은 해답이 없을 수도 있지만, 해답이 있을 때

${\displaystyle x_{m}=Tx_{0},}$

T와 함께 이득이라 불리는 R의 원소.

연속 제거

이 구간은 확장이 필요하다.추가하면 도움이 된다.(2012년 5월)

리턴 루프 방법

메이슨의 통치에 대한 몇 가지^[2] 명확한 일반화가 있다.^{[clarification needed]}가장 일반적인 방법은 리턴 루프 방식(전방 리턴 루프 방식(FRL이라고도 함)으로 이중 리턴 루프 방식(BRL)이 있다.첫 번째 엄격한^{[clarification needed]} 증거는 리글에게 귀속되기 때문에 리글의 규칙이라고 부르기도 한다.^[2][6]

메이슨의 규칙과 마찬가지로, 이러한^{[clarification needed]} 이득 표현은 그래프-이론적 방식(루프-게인, 경로 제품 등)으로 용어를 결합한다.그들은 임의의 비협조적인 고리 위에 그리고 정규 표현식의 줄 위에 있는 것으로 알려져 있다.^[5]

형식 설명

메소드는^{[clarification needed]} j${\displaystyle }$paths {\$displaystyle \in }$에 의해 인덱싱된 ^{[clarification needed]}입력에서 출력까지의 모든 경로를 열거하는 것으로 시작한다. 우리는 다음과 같은 정의를 사용한다.

• j-th 경로 제품은 (표기법 남용에 의한) k_j 에지 중량의 튜플이다.

${\displaystyle p_{j}=(w_{k_{j}^{(j)},\ldots,w_{2}^{{2}^{(j)}).}$^{[필요하다]}

• 꼭지점 v를 분할하는 것은 그것을 소스로 대체하고 원래의 발생률과 가중치를 존중하여 싱크하는 것이다(이는 출처를 취하고 v로 가라앉는 그래프 형태론의 역이다).
• 서브그래프 H의 루프 게인은 H에 포함되지 않은 모든 정점을 제거한 후 v에서 분할된 신호 흐름 그래프의 소스로부터 싱크까지의 게인이다.
• 각 경로는 그것을 따라 정점의 순서를 정의한다.이동 경로 j, i번째 FRL(BRL) 노드 계수는 (1-S_i^(j))⁻¹이며, 여기서_i^(j) S는₀ (뒤)의 (뒤) 정점과 v를 제거하여 얻은 하위 그래프를 따라 i번째 정점의 루프 이득이다.

이득에 대한 j-th 경로의 기여는 경로에 따른 제품이며, 경로 제품 중량과 노드 요인 간에 교대된다.

${\displaystyle T_{j}=\prod _{i=k_{j}}^{1}(1-S_{i}^{(j)}^{-1}w_{i}^{j}}}}}}}$

그래서 총 이득은

${\displaystyle T=\sum _{j\in J}T_{j}.}$

예

표시된 신호 흐름 그래프를 고려하십시오.x부터 z까지, (d)와 (e,a)의 두 가지 경로 제품이 있다.(d)를 따라, FRL과 BRL 기여도는 양쪽이 동일한 루프 게인을 공유함에 따라 일치한다(이러한 분할은 아래 표의 오른쪽 상단에 다시 나타난다).

${\displaystyle f+e(1-b)^{-1}c,}$

노드 팩터와 경로 가중치를 곱하면 이득 기여도는 다음과 같다.

${\dplaystyle T_{d}=\left[1-f-e(1-b)^{-1}c\오른쪽]^{-1}d.}$

경로(e,a), FRL과 BRL은 약간 다르며, 각각 아래 표와 같이 정점 y와 z가 뚜렷하게 갈라져 있다.

노드 요인과 경로 가중치의 교번 산물인_d T에 더하면 두 가지 게인 식을 얻을 수 있다.

${\displaystyle T^{(FRL)}=\왼쪽[1-f-e(1-b)^{-1-1}c\오른쪽]^{-1d+\왼쪽[1-f-e(1-b)^{-1e(1-b)^{-1e(1-b)^{-1}a,},}$

그리고

${\displaystyle T^{(BRL)}=\왼쪽[1-f-e(1-b)^{-1-1}c\오른쪽]^{-1d+(1-f)^{-1e\왼쪽[1-b-c(1-f)^{e}\오른쪽]^{-1}a,}$

이러한 값은 ID(ab)⁻¹ = ba⁻¹⁻¹ 및 a(1-ba)=(⁻¹1-ab)⁻¹a를 사용하여 동일하다고 쉽게 볼 수 있다.

적용들

행렬 신호 흐름 그래프

방정식 고려

${\displaystyle y_{i}=\sum _{j=1}^{2}a_{ij}x_{j}+\sum _{j=1}^{2}b_{ij}y_{j}}}}}}}}}}}}$

그리고

${\displaystyle z_{i}=\sum _{j=1}^{2}c_{ij}y_{j}}}}$

이 시스템은 다수의 입력과 출력이 있는 스칼라 신호 흐름 그래프로 모델링될 수 있다.그러나 변수는 자연스레 층으로 떨어져 벡터 x=(x₁,x₂)^t y=(y₁,y₂),^t z=(z₁,z₂)로 수집할 수 있다.^t이로 인해 기사의 상단에 있는 그림에 표시된 것처럼 훨씬 간단한 매트릭스 신호 흐름 그래프가 생성된다.

전진 리턴 루프 방식을 적용하는 것은 단일 경로 제품(C,A)이 있고 단일 루프 게인 B가 y에 있기 때문에 사소하다.따라서 매트릭스로서 이 시스템은 입력-출력 맵을 매우 콤팩트하게 표현하고 있다.

${\displaystyle T=C(1-B)^{-1}A.}$

유한 오토마타

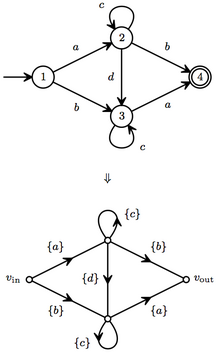
중요한 종류의 비전속 신호 흐름 그래프는 알파벳 $[\displaystyle \Sigma }$에 대한 유한 상태 자동이다$.$^[3][4]

직렬 연결은 단어의 결합에 해당하며, 자유단조 ${\$ $^\{*\}\}$의 하위 집합으로 확장할 수 ${\displaystyle {\mathrm{}}^{}}$. A의 경우, B${\displaystyle }$⊆ { { $\$

$A,b,b\cdot B=\{ab\mid a\in B\}}$

병렬 연결은 설정된 결합에 해당하며, 이 맥락에서 종종 A+B라고 쓰여진다.

마지막으로 셀프 루프는 자연스럽게 클라인 폐쇄에 대응한다.

${\displaystyle A^{*}=\{\lambda \}+A+AA+AAA+\cdots ,}$

여기서 $\lambda {\displaystyle }$ ${\displaystyle \lambda }$은(는) 빈 단어다.무한 기하학 계열과의 유사성

${\displaystyle (1-x)^{-1}=1+x+x^{2}+x^{3}}\cdots,}$

이 형식의 표현은 이 의미에서의 '반전'으로 작용하기 때문에 피상적인 것 이상이다.^[7]

이러한 방법으로 이 세 가지 연산 중 거의 대부분에서 빌드된$$ ${\$의 하위 집합을 정규식의 의미와 함께 식별할 수 있다.마찬가지로 $\sigma {\displaystyle {\mathrm{}}^{}}$ $∗{\$^{*}의 부분 집합에 의해 가장자리가 가중되는 유한 그래프도 그림에서와 같이 일반적으로 그 이론은 싱글톤 집합에서 시작되지만 유한한 오토마타로 식별할 수 있다$$.

이 오토매틱은 결정론적이어서 우리는 말로 경로를 분명히 열거할 수 있다.Return 루프 방법을 사용하여 경로 기여도는 다음과 같다.

• 경로 ab에는 노드 요인(c^*, $\lambda {\displaystyle }$ ${\displaystyle \lambda }$ )이 있으며,$$ 이로 인해 이득 기여가 발생함

${\displaystyle ac^{*}b,}$

• 경로 ada는 노드 요인(c^*, c^*, c, $\lambda {\displaystyle }$, ${\displaystyle \lambda }$ )을 가지고 $$있어 이득 기여를 한다.

${\displaystyle ac^{*}dc^{*a,}$

• 경로 ba에는 노드 인자(c^*, $\lambda {\displaystyle }$ ${\displaystyle \lambda }$ )가 있어 $$이득 기여가 있음

${\displaystyle bc^{*}a.}$

따라서 이 자동화에 의해 받아들여지는 언어(신호 흐름 그래프의 이득)는 이 용어들의 합이다.

${\displaystyle L=ac^{*}b+ac^{*}dc^{*a+bc^{*}a.}$

기록 노트

이 구간은 확장이 필요하다.추가하면 도움이 된다.(2012년 5월)

참고 항목

• 신호 흐름 그래프
• 메이슨 법칙
• 유한오토마타
• 정규식

메모들

참조

• Andaloussi, C.; Chalh, Z.; Sueur, C. (2006). "Infinite zero of linear time varying bond-graph models: Graphical rules". Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications. pp. 2962–2967. doi:10.1109/CACSD-CCA-ISIC.2006.4777109.
• Book, Ronald; Even, Shimon; Greibach, Sheila; Ott, Gene (1971). "Ambiguity in graphs and expressions" (PDF). IEEE Transactions on Computers. IEEE. 100 (2): 149–153. doi:10.1109/t-c.1971.223204. S2CID 20676251.
• Brzozowski, J.A.; McCluskey Jr., E.J. (1963). "Signal flow graph techniques for sequential circuit state diagrams". IEEE Transactions on Electronic Computers. IEEE (2): 67–76. doi:10.1109/PGEC.1963.263416.
• Greibach, Sheila (1965). "A new normal-form theorem for context-free phrase structure grammars". Journal of the ACM. ACM. 12 (1): 42–52. doi:10.1145/321250.321254. S2CID 12991430.
• Kuich, Werner; Salomaa, Arto (1985). Semirings, automata and languages. Springer-Verlag.
• Lorens, Charles S. (1964). Flowgraphs: For the Modeling and Analysis of Linear Systems. McGraw-Hill.
• Pliam, John; Lee, E. Bruce (1995). "On the global properties of interconnected systems". IEEE Transactions on Circuits and Systems I: Fund. Theory and Apps. IEEE. 42 (12): 1013–1017. doi:10.1109/81.481196.
• Riegle, Daryle; Lin, P.M. (1972). "Matrix signal flow graphs and an optimum topological method for evaluating their gains". IEEE Transactions on Circuit Theory. IEEE. 19 (5): 427–435. doi:10.1109/tct.1972.1083542.