모듈식 분해

그래프 이론에서 모듈 분해는 그래프를 모듈이라 불리는 정점의 하위 집합으로 분해하는 것이다.모듈은 그래프의 연결된 구성요소를 일반화한 것이다.그러나 연결된 구성 요소와는 달리 한 모듈은 다른 모듈의 적절한 하위 집합이 될 수 있다.따라서 모듈들은 단순히 파티션 대신 그래프를 반복적으로 분해(계층적)하게 된다.

방향을 잡지 않은 그래프와 지시된 그래프를 위한 모듈식 분해의 변형들이 있다.각 방향 지정되지 않은 그래프에 대해 이 분해는 고유하다.

이 개념은 다른 구조(예: 지시된 그래프)로 일반화될 수 있으며, 일부 그래프 클래스의 인식, 비교가능성 그래프의 전이적 방향 찾기, 그래프 최적화 문제, 그래프 도면에 대한 효율적인 알고리즘을 설계하는 데 유용하다.

모듈

모듈의 개념이 많은 영역에서 재발견됨에 따라 모듈들은 자율 집합, 동질 집합, 안정 집합, 집단 집합, 위원회, 외부 관련 집합, 간격, 비경시적 하위 네트워크, 부분적 집합(Brandstédt, Le & Spinrad 1999)이라고도 불려왔다.아마도 이들에 대한 가장 초기의 언급과 모듈형 인용구에 대한 첫 번째 설명과 그들이 야기하는 그래프 분해는 (갈라이 1967)에 나타나 있었다.

그래프의 모듈은 연결된 구성요소를 일반화한 것이다.$연결$된 구성 요소는 고정점의 $X$ ${\displaystyle$ X$}$ $세트$라는 속성을 가지므로 X ${\displaystyle$ X}의 모든 구성원이 $X{\displaystyle }$ ${\displaystyle$ X$}$에 없는 모든 정점의 비근접 구성$$ 요소$($이 속성을 가진 경우만 해당)가 된다.보다 일반적으로, X$${\$displaystyle$X}의 각 ${\displaystyle \mathrm{꼭지점}}$ v${\displaystyle }$x X$${\$displaystyle$ v$\not \in$X$\}$에 $대해{\displaystyle }$ X ${\$$displaystyle$ x$}$의 모든 $멤버$가 v$${\$displaystyle$ v$$$}$의 인접인$$ $경우{\displaystyle }$$$X$${\$displaystystyle v}$은 모듈이다$.$

마찬가지로 $X{\displaystyle }$ ${\displaystyle X}$의 모든 멤버가 $X{\displaystyle }$ ${\displaystyle X}$에 없는 꼭지점 중 이웃의 집합이 동일한$$ 경우 X ${\$displaystyle X$}$은 모듈이다$.$

연결된 구성 요소와는 반대로, 그래프의 모듈은 보완의 모듈과 동일하며, 모듈은 "내포"될 수 있다. 즉, 한 모듈은 다른 모듈의 적절한 하위 집합이 될 수 있다.그래프의 $정점$ V$${\$displaystyle V}$이(가) 하나의 기본 하위 집합과 빈 집합과 마찬가지로 모듈이며, 이를 사소한 모듈이라고 한다.그래프에는 다른 모듈이 있을 수도 있고 없을 수도 있다.그래프는 모든 모듈이 사소한 경우 prime이라고 불린다.

이러한 차이에도 불구하고 모듈은 연결된 $구성요소{\displaystyle }$ X {\$displaystyle X}$이(가$$) 유도하는 ${\displaystyle \mathrm{하위그래프}}$ G${\displaystyle }$[${\displaystyle }$X$$$]$ {\$displaystyle G[$X]}의 많은 속성이 그래프의 나머지 부분과 독립적이라는$$ 바람직한 속성을 보존한다.모듈에서 유도하는 서브그래프에도 유사한 현상이 적용된다.

따라서 그래프의 모듈은 알고리즘적인 관심이 크다.모듈 분해의 예가 되는 중첩된 모듈 세트를 사용하여 비교가능성 그래프의 인식 및 변환 방향, 순열 그래프의 순열 표현 인식 및 찾기, 그래프가 cograph a인지 여부를 인식하는 것과 같은 많은 조합 문제의 재귀적 해결책을 그래프로 안내할 수 있다.nd 질문에 대한 답변 인증서 찾기, 구간 그래프 인식 및 구간 표현 찾기, 거리-계통 그래프 정의(Spinrad, 2003), 그래프 그리기용(Papadopulos, 2006)그들은 완벽한 그래프 정리에 대한 로바스의 유명한 증거에 중요한 역할을 한다(골룸빅, 1980).

거리-계통 그래프와 원 그래프를 인식하는 경우 분할 분해라고 하는 모듈식 분해의 추가 일반화가 특히 유용하다(Spinrad, 2003).

위의 정의에서 모호성의 가능성을 피하기 위해, 우리는 다음과 같은 모듈의 공식 정의를 제공한다.${\displaystyle G}$=${\displaystyle }$( ${\displaystyle V}$, ${\displaystyle E}$) ${\displaystyle$ G$=(V,E$ $M{\displaystyle }$ ${\displaystyle \subseteq }$ V ${\displaystyle M\subseteq V}$은 $다음$과 같은 경우$$ G ${\displaystyle G}$의 모듈이다.

• the vertices of ${\displaystyle M}$ cannot be distinguished by any vertex in ${\displaystyle V\backslash M}$, i.e., ${\displaystyle \forall u,v\in M,\forall x\in V\backslash M}$, either ${\displaystyle x}$ is adjacent to both ${\displaystyle u}$ and ${\displaystyle v}$ or $$${\displaystyle x}$ ${\displaystyle x}$은(는) $u{\displaystyle }$ ${\$$displaystyle u}$에 인접하지 않으며 v {\$displaystyle$ v$}$에도 $인접$하지 않음$.$
• $M{\displaystyle }$ ${\displaystyle M}$의 꼭지점에는 동일한 외부 이웃 집합이$$ 있다. 즉,${\displaystyle \mathrm{}u}$ ${\displaystyle u,}$ ${\displaystyle v}$m${\displaystyle }$M, ${\displaystyle N}$ (${\displaystyle u}$ )${\displaystyle }$∖${\displaystyle }$M =${\displaystyle N}$ ( )${\displaystyle m}$ M ${\display$ style \$for u,v\in M,N(u)\setminus M=N(v)\setminus M$

${\displaystyle \mathrm{\varnothing }}$ ${\displaystyle \emptyset$ $\},$ $V{\displaystyle }$ ${\displaystyle$ $V}$ 및$$ $V{\displaystyle }$ ${\displaystyle \in }$ V ${\displaystyle$$\{v\}}}$에 대한 모든 단골격은 모듈이며, 사소한 모듈이라고 불린다.모든 모듈이 사소한 것이라면 그래프는 프라임이다.그래프 $G{\displaystyle }$ ${\displaystyle G}$또는 그 보완 그래프의 연결된 구성 요소도 $G{\displaystyle }$ ${\displaystyle G}$의 모듈이다$.$

${\displaystyle M}$ is a strong module of a graph ${\displaystyle G}$ if it does not overlap any other module of ${\displaystyle G}$: ${\displaystyle \forall M'}$ module of ${\displaystyle G}$, either ${\displaystyle M\cap M'=\emptyset }$ or ${\displaystyle M\subseteq$$M'}$ 또는$$ $M{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\displaystyle \subseteq }$ ${\displaystyle M}$ ${\displaystyle$ M$'\subseteq$ M$\}.$

모듈형 인용구 및 요인

$X{\displaystyle }$ ${\displaystyle X}$과 Y ${\displaystyle Y}$이(가) 분리 모듈인$$ 경우, $X{\displaystyle }$ ${\displaystyle X}$의 모든 구성원이 Y ${\displaystyle$ $Y$$}$의 모든 요소의 이웃이거나$,$ $X{\displaystyle }$$$${\$$displaystyty$ $X}$의 구성원이 $}$의 어떤 구성원과도 인접하지$$ 않음을 쉽게 알 수 있다$.$ 따라서 관계가 없다.두 개의 분리 모듈 사이의 ip는 인접하거나 인접하지 않다.이 두 극단 사이에 어떤 관계도 존재할 수 없다.

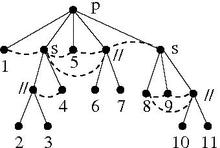
이 때문에 각 파티션 클래스가 모듈인$$ $V{\displaystyle }$ ${\displaystyle V}$의 모듈 파티션이 특히 관심사다.$P{\displaystyle }$ ${\displaystyle P}$이(가) 모듈식 파티션이라고 가정하십시오.Since the partition classes are disjoint, their adjacencies constitute a new graph, a quotient graph ${\displaystyle G/P}$, whose vertices are the members of ${\displaystyle P}$. That is, each vertex of ${\displaystyle G/P}$ is a module of G, and the adjacencies of these modules are the edges of ${\displaystyle G/P}$$(\displaystyle G/P$

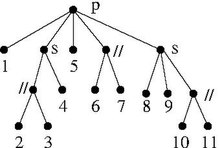
아래 그림에서 정점 1, 정점 2~4, 정점 5, 정점 6과 7, 정점 8~11은 모듈식 파티션이다.오른쪽 상단 다이어그램에서 이들 집합 사이의 가장자리는 이 분할에 의해 주어진 몫을 나타내고, 반면에 집합의 내부 가장자리는 해당 요인을 나타낸다.

파티션$$${\displaystyle }${${\displaystyle V\}}$ ${\displaystyle \{V\}$ 및 {${\displaystyle }$x${\displaystyle }$} ${\displaystyle x}$ ${\displaystyle \in }$ ${\displaystyle V}$ ${\displaystyle \}}$ ${\displaystyle \{x\} x\in$ V$\}$은(는) 사소한 모듈형 파티션이다.${\displaystyle G}$/${\displaystyle }${ ${\displaystyle V}$} ${\displaystyle$ G$/\{V\}}$은(는) 하나의 버텍스 그래프일$$ 뿐이고, $G{\displaystyle }$/${\displaystyle }${${\displaystyle }$x${\displaystyle }$} x${\displaystyle \}V}$ $}$ = G {\$displaystyle$G/\{$x\} x$\${\displaystyle \mathrm{in}}$ $V\}=G$ $X{\displaystyle }$ ${\\displaystystyle X}$은 비교 모듈이라고 가정합시다.그러면 $X{\displaystyle }$ ${\displaystyle$ X$}$과($)$ V ${\displaystyle \mathrm{\setminus }}$ X {\$displaystyle V\backslash$ X$}$의 단일 요소 하위 집합은 $V{\displaystyle }$ ${\displaystyle V}$의 비경쟁적 모듈 파티션이다$.$ 따라서 비경쟁적 모듈의 존재는 비경쟁적 모듈 파티션의 존재를 암시한다.일반적으로 $P{\displaystyle }$ ${\displaystyle P}$의 많은 또는 모든 구성원은 비독점적 모듈일$$ 수 있다.

$P{\displaystyle }$ ${\displaystyle P}$이(가) 비종교적 모듈형 파티션이라면 G/$P{\displaystyle }$${\displaystyle G/P$}은$($는) P ${\$$displaystyle$ $P}$의 서로 다른 파티션 클래스에 끝점이 있는 모든 가장자리를 압축적으로 표현한 것이다$.$ $P{\displaystyle }$ {\$displaystystyle$ P}의 각 파티션 클래스 $X{\displaystyle }$ ${\$에 $대해{\displaystyle }$ 하위 그래프 G $]$$X{\displaystyle }$ ${\displaystyle X}$이(가) 유도하는$$ 디스플레이 $스타일 G[X]}$을(를) 인수라고 하며 두 $끝점$을$$모두 X {\$displaystyle X}$로 나타내므로 $G{\displaystyle }$ ${\displaystyle G}$의 가장자리는 지수 $그래프{\displaystyle }$ G${\displaystyle /P}$ ${\displaystyle G/P}$와 그 요인만 주어 재구성할$$ 수 있다$.$prime graph라는 용어는 prime graph가 사소한 인용구와 요인만을 가지고 있다는 사실에서 유래한다.

$G{\displaystyle }$[ ${\displaystyle X}$ ${\displaystyle ]}$ ${\displaystyle G[X]}$이(가) 모듈형 지수 $G{\displaystyle /P}$ ${\displaystyle$ G$/P}$의 인자인$$ 경우 G${\displaystyle }$[ ${\displaystyle X}$ ${\displaystyle ]}$ ${\displaystyle G[X]}$이(가) 인자와 인수로 재분할 수 있다$$$.$각 재귀의 레벨은 지수를 상승시킨다.기본 사례로서 그래프에는 꼭지점이 하나만 있다.집합적으로 $G{\displaystyle }$ ${\displaystyle G}$은(는) 아래에서 위로 인자를 재구성하여 각 레벨의 인자와 인자를 결합하여 분해 단계를 역전시켜 귀납적으로 재구성할 수 있다$$.

아래 그림에서 그러한 재귀적 분해는 초기 모듈형 파티션의 인자를 더 작은 모듈형 파티션으로 재귀적으로 분해하는 한 가지 방법을 나타낸 트리로 표현된다.

그래프를 인자와 인수로 재귀적으로 분해하는 방법은 고유하지 않을 수 있다.(예를 들어, 전체 그래프의 정점의 모든 하위 집합은 모듈이며, 이는 그래프를 재귀적으로 분해하는 다양한 방법이 있다는 것을 의미한다.)어떤 방법은 다른 방법보다 더 유용할 수 있다.

모듈식 분해

다행히도, 모든 분해 방법을 암묵적으로 나타내는 그래프의 재귀적 분해(recursive discolation)가 존재한다. 이것이 모듈형 분해(modular discolation)이다.그것은 그 자체로 그래프를 반복적으로 시세로 분해하는 방법이지만 다른 모든 것을 잠식한다.아래 그림에 표시된 분해는 주어진 그래프에 대해 이 특별한 분해다.

다음은 모듈화 분해를 이해하는 데 있어 중요한 관찰 사항이다.

$X{\displaystyle }$ ${\$$displaystyle$ $X}$이(가) G ${\displaystyle G$$}$의 모듈이고 Y ${\displaystyle Y}$이(가$)$ X ${\$$displaystyle$ $X}$의 하위 집합인 경우$,$ $Y{\displaystyle }$ ${\$$displaystytle$ Y$}$은$$G}의 모듈이고, G [$X]$의 모듈인 경우에만 해당된다$.$

(갈라이, 1967)에서 갈라이는 다음과 같이 꼭지점 집합 $V{\displaystyle }$ ${\displaystyle V}$이$($가) 설정된 그래프에 모듈식 분해법을 반복적으로 정의했다.

1. 기본 사례로 $G{\displaystyle }$ ${\displaystyle$ G$}$에 꼭지점이 하나만 있으면 모듈식$$ 분해는 단일 트리 노드.
2. $G{\displaystyle }$ ${\displaystyle G}$이(가) 연결되어$$ 있고 그 보완도 $마찬가지$라면 V ${\displaystyle V}$의 적절한 하위 집합인 최대 모듈은 V ${\displaystyle V}$의 파티션이라고$$ Gallai는 보여주었다$.$그러므로 그것들은 모듈형 파티션이다.그들이 정의하는 지수는 프라임이다.트리의 루트에는 프라임 노드가 라벨로 표시되어 있으며, 이 $모듈들$은$$V {\$displaystyle$V}의 하위 모듈로 할당되어 있다$.$ 이 모듈들은 최대치이기 때문에 $지금$까지 표시되지 않은 모든 모듈은 V ${\displaystyle V}$의 $하위{\displaystyle }$ $X{\displaystyle }$ ${\displaystyle$ $X$$}$에 포함되어 있다$.$ $각{\displaystyle }$ 하위 X ${\displaystyle V$ replaystrac.모듈식 분해 트리가 $G{\displaystyle }$[ ${\displaystyle X}$ ${\displaystyle ]}$ ${\displaystyle G[X]}$인 $ing{\displaystyle }$ X ${\displaystyle X}$은$($는) 위의 키 관찰에 $의해{\displaystyle }$ G$${\$displaystyle G}$의 모든 모듈을 나타낸다$$.
3. $G{\displaystyle }$ ${\displaystyle G}$이(가) 분리되면$$ 해당 보완 장치가 연결된다.연결된 구성 요소의 모든 결합은 $G{\displaystyle }$ ${\displaystyle G}$의 모듈이다$.$ 다른 모든 모듈은 연결된 단일 구성 요소의 하위 집합이다.이는 연결된 구성 요소의 하위 세트를 제외한 모든 모듈을 나타낸다.각 구성 요소 $X{\displaystyle }$ ${\displaystyle X}$에 대해 G $[$ ${\displaystyle X}$ {\$displaystyle$ $G{\displaystyle }$[$X$의 모듈식 분해 트리로$$ $X{\displaystyle }$ {\$displaystyle X$$}$을(를$)$ 대체하는 것은 위의 키 관찰에 $의해{\displaystyle }$ G$${\$displaystyle G$의 모든 모듈을 나타낸다$$.트리의 루트는 평행 노드라는 레이블이 붙으며, 루트의 $자식$으로서 X ${\displaystyle X}$ 대신 부착된다.아이들이 정의한 몫은 완전한 그래프를 보완한 것이다.
4. $G{\displaystyle }$ ${\displaystyle G}$의 보수가 분리되면$$ G ${\displaystyle G}$이(가) 연결된다$$.$V{\displaystyle }$ ${\displaystyle V}$의 하위 트리인 하위 트리는 G ${\displaystyle G}$이(가) 분리된$$ 사례와 대칭되는 방식으로 정의되며$$, 이는 그래프의 모듈이 해당 보어의 모듈과 동일하기 때문이다.나무의 뿌리는 직렬 노드에 라벨이 붙어 있고, 아이들이 정의한 몫은 완전한 그래프다.

최종 트리는 베이스 케이스로 인해 $G{\displaystyle }$ ${\displaystyle G}$의 정점 세트를 잎으로 가지고$$ 있다.$G{\displaystyle }$ ${\displaystyle G}$ 정점의$$ Y {\$displaystyle$ Y$} 집합$은 트리 $노드{\displaystyle }$ 또는 직렬 또는 병렬 노드의 자식 결합인 경우에만 모듈이다$$.이것은 $암시적$으로 V ${\displaystyle V}$의 모든 모듈형 파티션을 제공한다$.$ 이러한 의미에서 모듈형 분해 $트리$는$$G {\$displaystyle$ G$}$을 재귀적으로 분해하는 다른 모든 방법을 "submesses"한다$$.

알고리즘 문제

모듈식 분해 트리를 나타내는 데이터 구조는 노드를 입력하고 노드가 $나타내는$ G ${\displaystyle G}$의 정점 집합을 반환하는 작업을 지원해야 한다.이를 위한 분명한 방법은 각 노드에 그것이$$ 나타내는 $K{\displaystyle }$ ${\displaystyle k}$ 꼭지점$$ 목록을 할당하는 것이다.노드에 포인터가 주어지면, 이 구조는 $O{\displaystyle \mathcal{}}$(${\displaystyle k}$ ) ${\displaystyle${\$mathcal {O}(k)}$시간에서$$ $나타내는$ G ${\displaystyle G}$의 꼭지점 집합을 반환할 수 있다.그러나 이 데이터 구조에는 최악의 경우 $\theta {\displaystyle \mathrm{}({}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$) ${\displaystyle \Teta(n^{2})$ 공간이$$ 필요하다.

이 성능과 일치하는 $O{\displaystyle \mathcal{}}$(${\displaystyle n}$) {\$displaystyle$ {\$mathcal{O}(n)}$ -공간$$ 대안은 모든 $표준{\displaystyle \mathcal{}}$O ($){\displaystyle${\$mathcal}{O}}($n$$) 루트 트리 데이터 구조를 사용하여 모듈식 분해 트리를 나타내고 각 잎에 다시$$ $사용$하는$$G {\$displaysty G}$의 꼭지점으로 라벨을 표시함으로써 얻을 수 있다.nts. 내부 노드 $v{\displaystyle }$ ${\displaystyle v}$이(가) 나타내는 집합은 잎 하위 그룹의 레이블 집합에 의해 주어진다$$.$k$ ${\displaystyle k}$ 잎이 있는 뿌리 트리는 최대 $k{\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle k-1}$개의 내부$$ 노드를 가지고 있다는 것은 잘 알려져 있다.$v{\displaystyle }$ ${\displaystyle v}$에서 시작하는 깊이 우선 검색을 사용하여$$ $v{\displaystyle }$ ${\displaystyle v}$의 잎-세속 레이블을 $O{\displaystyle \mathcal{}(k)}$ ${\displaystyle {\mathcal {O}(k)}$시간으로$$$$ 보고할 수 있다.

각 노드 $X{\displaystyle }$ ${\displaystyle X}$은(는) $G{\displaystyle }$ ${\displaystyle G}$의 꼭지점 $집합$이며, X$${\$displaystyle$ X$}$이(가) 내부 노드인 경우$,$ 설정된 P {\$displaystyle$ $P$$}$은 각 파티션 클래스가 $모듈$인 X ${\displaystyle$ X$}$의 $파티션$이다.They therefore induce the quotient ${\displaystyle G[X]/P}$ in ${\displaystyle G[X]}$. The vertices of this quotient are the elements of ${\displaystyle P}$, so ${\displaystyle G[X]/P}$ can be represented by installing edges among the children of ${\displaystyle X}$. If ${\displaystyle Y}$${\displaystyle Y}$ and ${\displaystyle Z}$ are two members of ${\displaystyle P}$ and ${\displaystyle u\in Y}$ and ${\displaystyle v\in Z}$, then ${\displaystyle u}$ and ${\displaystyle v}$ are adjacent in ${\displaystyle G}$ if and only if ${\displaystyle Y}$ and ${$$\displaystyle Z}$은(는) 이 지수에 인접해 있다$$.$G{\displaystyle }$ ${\displaystyle G}$의 꼭지점$$ $u},v\}$의 모든 쌍에 대해 모듈식 분해 트리에서${\displaystyle }${$}$ {\$displaystyle$\{$u\}$${\displaystyle }$및$$ {$}$ {\$displaystyle$\{$v\}}$의 최소 공통 조상의 자식에서 인수에 의해 결정된다$.$따라서, 이러한 방법으로 인수로 라벨을 붙인 모듈식 분해는 $G{\displaystyle }$ ${\displaystyle G}$의 완전한 표현을 제공한다$.$

$많은{\displaystyle }$ 조합문제는 G ${\displaystyle G}$에서 이러한 각 인용구에 대해 개별적으로 문제를 풀면 해결할$$ 수 있다.예를 들어 $G{\displaystyle }$ ${\displaystyle G}$은(는) 이러한 각 인수가 비교가능성 그래프인 경우에만 비교가능성 그래프다$$(갈라이, 67; 뫼링, 85).따라서 그래프가 비교가능성 그래프인지 아닌지를 알아내기 위해서는 각 인용구들이 비교가능성 그래프인지 여부만 알아내면 된다.실제로 비교가능성 그래프의 전이적 방향을 찾기 위해서는 모듈화 분해의 이러한 인용구(Galai, 67; Möhring, 85)를 각각 과도적으로 방향만 잡으면 된다(Galai, 67; Möhring, 85)순열 그래프(McConnell 및 Spinrad '94), 구간 그래프(Hsu 및 Ma '99), 완벽한 그래프 및 기타 그래프 클래스에도 유사한 현상이 적용된다.그래프의 중요한 조합 최적화 문제는 유사한 전략을 사용하여 해결할 수 있다(Möhring, 85).

Cographs는 모듈식 분해 트리에 병렬 또는 직렬 노드만 있는 그래프다.

그래프의 모듈식 분해 트리를 계산하는 최초의 다항 알고리즘은 1972년(제임스, 스탠튼 & 코원 1972)에 발표되었으며, 이제 선형 알고리즘을 사용할 수 있다(McConnell & Spinrad 1999, Tedder et al. 2007, Cournier & Habib 1994).

일반화

지시된 그래프의 모듈식 분해는 선형 시간에 수행할 수 있다(McConnell & de Montgolfier 2005).

소수의 간단한 예외를 제외하고, 비교 모듈식 분해 기능이 있는 모든 그래프에도 스큐 파티션이 있다. (Red 2008)

참조

• Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy P. (1999). Graph Classes: A Survey. Society for Industrial and Applied Mathematics. doi:10.1137/1.9780898719796. ISBN 978-0-89871-432-6.
• Gallai, Tibor (1967). "Transitiv orientierbare Graphen". Acta Mathematica Academiae Scientiarum Hungaricae. 18 (1–2): 25–66. doi:10.1007/BF02020961. MR 0221974. S2CID 119485995.
• James, Lee O.; Stanton, Ralph G.; Cowan, Donald D. (1972). "Graph decomposition for undirected graphs". Proc. 3rd Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1972). Florida Atlantic University. pp. 281–290. MR 0351909.
• Golumbic, Martin C. (1980). Algorithmic Graph Theory and Perfect Graphs. Academic Press. ISBN 0-444-51530-5.
• Hsu, W.L.; Ma, T. (1999). "Fast and simple algorithms for recognizing chordal comparability graphs and interval graphs". SIAM Journal on Computing. 28 (3): 1004–1020. CiteSeerX 10.1.1.104.4647. doi:10.1137/S0097539792224814.
• McConnell, Ross M.; de Montgolfier, Fabien (2005). "Linear-time modular decomposition of directed graphs". Discrete Applied Mathematics. 145 (2): 198–209. doi:10.1016/j.dam.2004.02.017.
• McConnell, Ross M.; Spinrad, Jeremy P. (1999). "Modular decomposition and transitive orientation" (PDF). Discrete Mathematics. 201 (1–3): 189–241. doi:10.1016/S0012-365X(98)00319-7. MR 1687819.
• Möhring, Rolf H. (1985). I. Rival (ed.). "Algorithmic aspects of comparability graphs and interval graphs". Graphs and Order. D. Reidel: 41–101. doi:10.1007/978-94-009-5315-4_2. ISBN 978-94-010-8848-0.
• Möhring, Rolf H. (1985). "Algorithmic aspects of the substitution decomposition in optimization over relations, set systems and Boolean functions". Annals of Operations Research. 4: 195–225. doi:10.1007/BF02022041. S2CID 119982014.
• Papadopoulos, Charis; Voglis, Constantinos (2005). "Drawing graphs using modular decomposition" (PDF). Proc. 13th International Symposium on Graph Drawing (GD'05). Lecture Notes in Computer Science. Vol. 3843. Springer-Verlag. pp. 343–354. doi:10.1007/11618058_31. MR 2229205.
• Reed, Bruce (2008). "Skew partitions in perfect graphs" (PDF). Discrete Applied Mathematics. 156 (7): 1150–1156. doi:10.1016/j.dam.2007.05.054. MR 2404228. Archived from the original (PDF) on 2015-09-19. Retrieved 2012-08-13.
• Spinrad, Jeremy P. (2003). Efficient Graph Representations. Fields Institute Monographs. American Mathematical Society. ISBN 0-8218-2815-0.
• Tedder, Marc; Corneil, Derek; Habib, Michel; Paul, Christophe (2008). "Simpler Linear-Time Modular Decomposition Via Recursive Factorizing Permutations". Proc. 35th International Colloquium on Automata, Languages and Programming (ICALP 2008). Lecture Notes in Computer Science. Vol. 5125. Springer-Verlag. pp. 634–645. arXiv:0710.3901. doi:10.1007/978-3-540-70575-8_52.
• Zahedi, Emad; Smith, Jason (31 July 2019). "Modular Decomposition of Graphs and the Distance Preserving Property". Discrete Applied Mathematics. 265 (7): 192–198. arXiv:1805.09853. Bibcode:2018arXiv180509853Z. doi:10.1016/j.dam.2019.03.019.

외부 링크

• 모듈식 분해 알고리즘의 Perl 구현
• 모듈식 분해 알고리즘의 자바 구현
• 모듈화 분해 알고리즘의 Julia 구현