생쥐 문제

수학에서 생쥐 문제는 다수의 생쥐(혹은 곤충, 개, 미사일 등)가 일반 다각형의 모서리에 배치되는 것으로 간주되는 연속적인 추격-탈진 문제다.고전적인 설정에서 각각은 바로 인접한 위치(시계 방향 또는 시계 반대 방향)를 향해 움직이기 시작한다.목표는 종종 그 쥐들이 몇 시에 만나는지 알아내는 것이다.

가장 일반적인 버전은 유닛 사각형의 모서리에서 시작하여 유닛 속도로 움직이는 마우스를 가지고 있다.이 경우 그들은 한 단위의 시간 후에 만난다. 왜냐하면 이웃한 두 생쥐 사이의 거리는 항상 한 단위의 속도로 감소하기 때문이다.n의 unit-length 면{n\displaystyle}정다각형을 위해 1−. 왜냐하면⁡(2π/n){1-\cos(2\pi /n)\displaystyle}의 속도로 더 일반적으로, 이웃의 쥐들 사이의 거리 감소한다, 그래서 그들은 1/(1−. 왜냐하면 ⁡(2π/n)){\displaystyle 1/{\bigl(}1-\cos(2\pi /n){\bigr)}의 시간 후에 만나}.[1]는 경우.2]

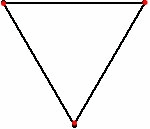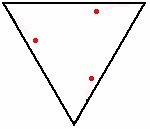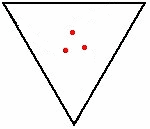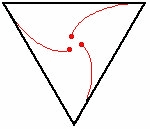
쥐의 경로

모든 일반 다각형에 대해, 각 마우스는 로그 나선형 모양의 추적 곡선을 추적한다.이 곡선은 다각형의 중심에서 만난다.^[3]

미디어에서

다라오브라이인에서: Hard Sums 학교, 생쥐 문제가 논의되었다.생쥐 4마리 대신 볼룸 댄서 4마리가 사용된다.^[4]

참조

외부 링크

• 제노의 생쥐 문제와 로그 나선형 - 방정식 도출이 있는 유튜브 강의