키쿠치 선(물리학)

Kikuchi lines (physics)
키쿠치 선은 육각23 사파이어(AlO)의 300 keV 전자에 대해 1/1å까지 쌍을 이루며, 일부 교차로에는 라벨이 붙어 있다.

키쿠치 선은 산란으로 형성된 전자의 무늬다.그들은 짝을 지어 단일 결정 표본에서 전자 회절의 띠를 형성하고, 거기서 그들이 보고 있는 것이 불확실한 현미경학자들에게 "방향 공간의 도로" 역할을 한다.전송 전자현미경에서 그것들은 다중 산란을 충분히 할 수 있을 정도로 두꺼운 표본의 영역에서 쉽게 회절된다.[1]기쿠치 밴드는 크리스털을 기울이면서 깜빡이는 회절점(회절점)과 달리 교차로(구역이나 극이라 불림)와 한 교차로에서 다음 교차로로 연결되는 경로가 잘 정의된 방향공간을 표시한다.

키쿠치 밴드 기하학의 실험적이고 이론적인 지도와 그 직공간 아날로그(예: 굽힘 윤곽, 전자 채널링 패턴, 프린지 가시성 지도)는 결정체와 나노크리스탈린의 전자 현미경 검사에서 점점 더 유용한 도구다.[2]각 기쿠치 선은 격자 평면의 한 쪽에서 브라그 회절과 연관되기 때문에, 이 선들은 개별 회절 지점을 식별하는 데 사용되는 동일한 밀러 또는 상호 격자 지수로 라벨을 붙일 수 있다.반면 키쿠치 밴드 교차로 또는 구역은 직격 지수(즉, 격자 기준 벡터 a, b, c의 정수 배수를 나타내는 지수)로 지수화된다.

키쿠치 선은 열원자 진동의 결과처럼 산란된 전자를 분산시켜 회절 패턴으로 형성된다.[3]이들을 정량적으로 이해하기 위해서는 확산 비탄성 산란이라는 역동적 이론이 필요하지만,[4] 기쿠치 세이시가 1928년에 제안한 단순한 탄성 메커니즘에서 이들의 기하학의 주요 특징을 추론할 수 있다.[5]

X선 산란에서는 이러한 선을 코셀 선[6](Walther Kosel의 이름을 따서 명명)이라고 한다.

실험용 키쿠치 패턴 및 지도 기록

300 keV 전자빔으로 찍은 단일 결정 실리콘의 수렴 빔 회절 패턴의 키쿠치 선

왼쪽 그림은 (004) 기쿠치 밴드를 따라 구역에서 약 7.9° 떨어진 빔 방향으로 취한 실리콘[100] 구역으로 통하는 키쿠치 라인을 보여준다.영상의 동적 범위는 필름의 일부분만 과도하게 노출되지 않을 정도로 크다.키쿠치 선은 비록 눈과 사진 매체 모두 조도에 대한 대략적인 로그 반응을 가지고 있음에도 불구하고, 종이나 필름에 움직이지 않는 것을 캡처하는 것보다 형광 스크린에 어두운 적응의 눈으로 따라 하기 훨씬 쉽다.따라서 그러한 회절 기능에 대한 완전한 정량적 연구는 CCD 검출기의 큰 선형 동적 범위에 의해 지원된다.[7]

이 이미지는 10° 이상의 각도 범위와 일반적인 카메라 길이보다 짧은 L의 사용을 필요로 한다.키쿠치 밴드 폭 자체(거의 roughL/d는 해당 평면에 대한 Bragg 각도의 약 2배인 electronsL/d)는 전자 파장 97(이 경우 약 1.97 피코미터)이 격자 평면 d스페이스 자체보다 훨씬 작기 때문에 1°보다 훨씬 낮다.비교를 위해, 실리콘(022)의 d-스페이스는 약 192피코미터인 반면, 실리콘(04)의 d-스페이스는 약 136피코미터다.

비탄성 평균 자유 경로(약 200나노미터)보다 두꺼운 결정 영역에서 이미지를 추출해 확산 산란 특징(키쿠치 선)이 일관성 있는 산란 특징(분산점)에 비해 강하도록 했다.디스크가 밝은 키쿠치 선과 교차하면서 살아남은 회절점이 나타난다는 것은 회절 패턴을 수렴성 전자빔으로 취했다는 뜻이다.실제로 기쿠치 선은 선택된 영역이나 수렴 빔 전자 회절 패턴의 두꺼운 영역에서 쉽게 볼 수 있지만, 크기(대신 격자-프링 가시성 효과가 중요해지는 대신) 100nm 미만의 결정에서 회절에서는 보기 어렵다.이 이미지는 수렴 빔으로 기록되었는데, 그것 또한 필름에 기록되어야 하는 대비의 범위를 감소시키기 때문이다.

스테레아디안보다 더 많이 커버하는 키쿠치 지도를 컴파일하려면 점진적으로만 변경되는 틸트(예: 각 방향으로 2°씩)에서 많은 영상을 촬영해야 한다.이것은 지루한 작업이 될 수 있지만, 3차원으로 격자 대칭이 명확하게 드러날 수 있기 때문에 알 수 없는 구조를 가진 결정체를 조사할 때 유용할 수 있다.[8]

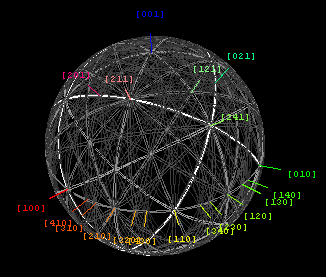
키쿠치 선 지도와 그 입체 투영

[001] 다이아몬드 얼굴 중심 큐빅 크리스털을 위한 구역 스테레오그래피 키쿠치 지도
FCC 결정에서 8개의 <111> 영역 중 4개 영역 사이의 틸트 트래버스 애니메이션

왼쪽 그림은 실리콘 방향 공간의 더 큰 부분을 위한 키쿠치 선을 표시한다.실리콘의 경우 하단에 있는 [011]과 [001] 구역 사이의 각도가 45°이다.오른쪽 하단의 네 개 영역(여기서 [001]이라는 레이블이 붙어 있음)은 위의 실험 패턴에서 [100]이라는 레이블이 붙어 있는 영역과 대칭과 방향이 동일하지만, 그 실험 패턴은 약 10°만 미분할 뿐이다.

또한 왼쪽 그림은 [001] 영역을 중심으로 한 입체 투영에서 발췌한 것이라는 점에 유의하십시오.그러한 등각 투영은 교차점의 국부 각도를 보존하면서 구면 표면의 조각을 평면에 매핑할 수 있게 한다.그러한 지도를 그리려면 곡률 반경이 매우 큰 원호를 그릴 수 있어야 한다.예를 들어, 왼쪽 그림은 컴퓨터가 등장하기 전에 그려진 것이므로 빔 나침반을 사용해야 했다.컴퓨터의 도움을 받아 곡률 반경이 큰 곡선을 그리기가 훨씬 쉽기 때문에 오늘날 빔 나침반을 찾는 것은 상당히 어려울 수 있다.

입체 플롯의 각도 보존 효과는 오른쪽 그림에서 더욱 뚜렷하게 나타나며, 이는 예를 들어 금이나 알루미늄과 같은 얼굴 중심 또는 입방체 밀폐 결정의 방향 공간의 180°를 완전히 소계한다.애니메이션은 <111> 영역 사이에 있는 얼굴 중심의 입방정정의 {220}개의 가장자리 가시성 대역을 따르며, 이때 60° 지점 회전으로 원래 시퀀스의 반복을 통해 다음 <111> 영역으로의 이동을 설정한다.프린지 가시성 대역은 키쿠치 대역과 동일한 글로벌 지오메트리를 가지지만 얇은 표본의 경우 폭이 d-스페이스에 비례한다.키쿠치 밴드로 실험적으로 얻을 수 있는 각도장 폭(및 틸트 범위)은 일반적으로 훨씬 작지만, 애니메이션은 키쿠치 밴드가 정보 결정학자들이 단일 결정 표본의 방향 공간에서 랜드마크 사이에서 길을 찾는 데 어떻게 도움을 주는지 광각도를 제공한다.

실제 공간 아날로그

실리콘 [100] 구부러진 윤곽 거미, 약 500나노미터 넓이의 타원형 영역 위에 갇힘

키쿠치 선은 두꺼운 표본의 회절 영상에서 격자 평면의 가장자리를 강조해 주는 역할을 한다.높은 에너지 전자의 회절에서 Bragg 각도가 매우 작기 때문에 (~)300 keV의 경우 1⁄4 도), 키쿠치 대역은 상호 공간에서는 상당히 좁다.이것은 또한 실제 공간 영상에서 격자 평면의 가장자리 온이 확산 산란 특징이 아니라 일관성 있는 산란과 관련된 대조적으로 장식된다는 것을 의미한다.이러한 일관성 있는 산란 특징에는 추가 회절(곡선 포일의 구부러진 윤곽에 대한 책임), 더 많은 전자 침투(결정 표면의 전자 영상 스캔에서 전자 채널링 패턴이 발생함), 격자 프린지 대비(빔 방향에 격자 프린지 강도의 의존성을 초래함)가 포함된다.검체 두께와 연결됨).대비 세부사항은 다르지만 이러한 특징과 기쿠치 지도에 대한 격자 평면 추적 기하학은 동일하다.

구부러진 윤곽선 및 흔들림 곡선

시료 두께 및 빔 기울기의 함수로 등고선 및 격자 프린지 가시성 구부리기

흔들의 곡선[9](왼쪽)은 입사 전자 빔 사이의 각도와 표본의 격자 평면 사이의 각도의 함수로서 산란 전자 세트의 그림이다.이 각도가 에지온(전자 빔이 격자 평면에 평행하고 정상과 수직으로 흐르는 방향)에서 어느 방향으로 변화하면, 빔은 Bragg 확산 상태로 이동하며 더 많은 전자가 현미경의 후방 초점 평면 구멍 밖으로 확산되어 보이는 다크 라인 쌍(밴드)이 발생한다.오른쪽 이미지에 표시된 구부러진 실리콘 호일의 이미지

이 이미지의 [100] 벤드 윤곽선 "스파이더"는 크기가 마이크로미터보다 작은 타원형 시계유리 모양의 실리콘 영역에 갇혀 300 keV 전자로 이미징되었다.수정을 기울이면 거미는 마치 나가려는 것처럼 타원형의 가장자리 쪽으로 움직인다.예를 들어, 이 이미지에서 거미의 [100] 교차점이 시료를 왼쪽으로 기울이면서 타원 우측으로 이동했다.

거미의 다리, 그리고 그 교차점은 위의 실험 기쿠치 패턴에 관한 섹션에서 [100] 부근의 기쿠치 패턴과 정확히 같은 방법으로 색인화할 수 있다.따라서 원칙적으로 이 구부러진 윤곽선을 사용하여 타원형의 모든 지점에서 포일의 벡터 기울기(밀리라디안 정확도 포함)를 모델링할 수 있다.

격자 프린지 가시성 맵

위의 흔들곡선에서 볼 수 있듯이, 표본 두께가 10나노미터와 더 작은 범위(예: 0.23nm에 가까운 300 keV 전자 및 격자 스페이스의 경우)로 이동할 때 회절 및/또는 격자-프링의 대비를 일으키는 틸트의 각도 범위는 표본 두께에 반비례하게 된다.따라서 격자-프링 가시성의 기하학은 단일 결정 시료(예: 10마이크로미터 범위에서 두께가 있는 금속 및 반도체 시료) 연구에 유용한 것처럼 나노물질의 전자현미경 연구에 유용하게 된다.[10][11]nanostructure에 예를 들어 응용:(나는)이미지를 무작위로 지향적 나노 입자의 다른 tilts,[12](ii)프린지 지문에서 찍은 사진에서 개별 나노 입자의 3D격자 매개 변수 결정을 포함한다,(iii)입자 두께 지도 기울기, 정 20면체 결연의(iv)탐지에 프린지 대비 변화에 기초하여.fr임의의 방향의 나노 입자의 격자 이미지 및 (v) 나노 입자와 원통형 지지대 사이의 방향 관계 분석.

전자 채널링 패턴

300keV 전자에 의한 브릴루인 존 구조

위의 기법들은 모두 얇은 시편을 통과한 전자의 검출, 대개 전송 전자현미경으로 이루어진다.반면에 전자현미경을 스캔하는 것은 보통 두꺼운 표본을 가로질러 집중된 전자빔을 발사할 때 "키워진" 전자를 본다.전자 채널링 패턴은 전자 현미경 2차 및/또는 백스캐터 전자 영상을 스캔할 때 나타나는 에지온 격자 평면과 관련된 대비 효과다.

대비 효과는 우선 구부러진 등고선의 경우와 유사하게 순서를 정하는 것이다. 즉, 확산 조건 하에서 결정 표면으로 들어가는 전자는 채널(에너지 손실 없이 시료 안으로 더 깊이 침투)하는 경향이 있고, 따라서 검출하기 위해 진입 표면 근처에서 더 적은 전자를 시동한다.따라서 현재 잘 알려진 키쿠치 선 지오메트리와 함께 빔/래티스 방향에 따라 밴드가 형성된다.

첫 번째 스캐닝 전자 현미경(SEM) 이미지는 실리콘 강철의 전자 채널링 대비 이미지였다.[13]그러나 일반적으로 마멸 손상 또는 비정형 코팅의 얇은 층만 대비를 모호하게 하는 데 적합하기 때문에 이 기법의 실용적 사용은 제한적이다.[14]검체가 충전을 방지하기 위해 검사 전에 전도성 코팅을 해야 하는 경우, 이 역시 대비를 모호하게 할 수 있다.쪼개진 표면과 원자 척도로 자체 조립된 표면에서 전자 채널링 패턴은 앞으로 몇 년 안에 현대 현미경으로 점점 더 많이 응용될 가능성이 있다.

참고 항목

참조

  1. ^ David B. Williams; C. Barry Carter (1996). Transmission electron microscopy: A textbook for materials science. Plenum Press, NY. ISBN 978-0-306-45324-3.
  2. ^ K. Saruwatari; J. Akai; Y. Fukumori; N. Ozaki; H. Nagasawa; T. Kogure (2008). "Crystal orientation analyses of biominerals using Kikuchi patterns in TEM". J. Mineral. Petrol. Sci. 103: 16–22.
  3. ^ Earl J. Kirkland (1998). Advanced computing in electron microscopy. Plenum Press, NY. p. 151. ISBN 978-0-306-45936-8.
  4. ^ S. Kikuchi (1928). "Diffraction of Cathode Rays by Mica". Japanese Journal of Physics. 5 (3061): 83–96. Bibcode:1928Natur.121.1019N. doi:10.1038/1211019a0.
  5. ^ P. Hirsch; A. Howie; R. Nicholson; D. W. Pashley; M. J. Whelan (1977). Electron microscopy of thin crystals. Butterworths/Krieger, London/Malabar FL. ISBN 978-0-88275-376-8.
  6. ^ R. W. James (1982). "Chapter VIII". The Optical Principles of the Diffraction of X-Rays'. Ox Bow Press, Woodbridge, Connecticut. ISBN 978-0-918024-23-7.
  7. ^ J. C. H. Spence and J. Zuo (1992). "Ch. 9". Electron microdiffraction. Plenum, New York. ISBN 978-0-306-44262-9.
  8. ^ E. Levine; W. L. Bell; G. Thomas (1966). "Further applications of Kikuchi diffraction patterns; Kikuchi maps". Journal of Applied Physics. 37 (5): 2141–2148. Bibcode:1966JAP....37.2141L. doi:10.1063/1.1708749.
  9. ^ H. Hashimoto; A. Howie; M. J. Whelan (1962). "Anomalous Electron Absorption Effects in Metal Foils: Theory and Comparison with Experiment". Proceedings of the Royal Society A. 269 (1336): 80. Bibcode:1962RSPSA.269...80H. doi:10.1098/rspa.1962.0164.
  10. ^ P. Fraundorf; Wentao Qin; P. Moeck; Eric Mandell (2005). "Making sense of nanocrystal lattice fringes". Journal of Applied Physics. 98 (11): 114308–114308–10. arXiv:cond-mat/0212281. Bibcode:2005JAP....98k4308F. doi:10.1063/1.2135414.
  11. ^ P. Wang; A. L. Bleloch; U. Falke; P. J. Goodhew (2006). "Geometric aspects of lattice contrast visibility in nanocrystalline materials using HAADF STEM". Ultramicroscopy. 106 (4–5): 277–283. doi:10.1016/j.ultramic.2005.09.005.
  12. ^ Wentao Qin; P. Fraundorf (2003). "Lattice parameters from direct-space images at two tilts". Ultramicroscopy. 94 (3–4): 245–262. arXiv:cond-mat/0001139. doi:10.1016/S0304-3991(02)00335-2. PMID 12524195.
  13. ^ Knoll M. (1935). "Aufladepotentiel und sekundäremission elektronenbestrahlter körper (Static potential and secondary emission of bodies under electron irradiation)". Z. Tech. Phys. 11: 467–475.
  14. ^ J. I. Goldstein; D. E. Newbury; P. Echlin; D. C. Joy; A. D. Romig Jr.; C. E. Lyman; C. Fiori; E. Lifshin (1992). Scanning electron microscopy and X-ray microanalysis. Plenum Press, NY. ISBN 978-0-306-44175-2.

외부 링크