커널 주성분 분석

다변량 통계학 분야에서 커널 주성분 분석(Kernel PCA)^[1]은 커널 방법의 기법을 이용한 주성분 분석(PCA)의 확장이다.커널을 사용하여 PCA의 원래 선형 연산은 재현 커널 힐버트 공간에서 수행된다.

배경: 선형 PCA

기존의 PCA는 제로 중심 데이터에서 작동한다는 점을 상기하십시오. 즉,

${\displaystyle \frac{\mathrm{1N}}{}}$ ${\displaystyle \sum \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{i}}}$= ${\displaystyle \underset{}{\overset{}{}}}$ x ${\displaystyle {}_{}}$= ${\displaystyle 0\mathbf{}}$ ${\${$x$}$_{i}=\mathbf {0$

여기서 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$는 $N{\displaystyle }$ ${\displaystyle N}$ 다변량$$ 관측치 중 하나이다.공분산 행렬을 대각선화하여 작동하며,

${\displaystyle C={\frac {1}{{N}\sum _{i=1}^{N}\mathbf {x} _{i}^{\top }}}}}$

즉, 공분산 행렬의 구성을 다음과 같이 제공한다.

${\displaystyle \lambda \mathbf {v} =C\mathbf {v}}$

라고 다시 쓸 수 있는.

${\displaystyle \lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}}~i=1,\ldots ,N}$.^[2]

(다음 항목 참조):선형 측정 시스템으로서의 공분산 행렬)

PCA에 커널 소개

커널 PCA의 효용, 특히 클러스터링을 이해하려면 일반적으로 N 지점은 < N ${\displaystyle d<N}$ 차원으로 선형 분리될 수 없지만, 거의 항상 $d{\displaystyle }$ ${\displaystyle \ge }$ ${\displaystyle N}$ ${\displaystyle d\geq N}$ 차원으로$$ 선형 분리될 수 있음을 관찰하십시오.즉, N개의 점이 ${\displaystyle {}_{}}$ x i ${\$을(를$)$ 사용하여 N차원 공간에 매핑하면

${\displaystyle \mathrm{\phi }}$( ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \Phi (\mathbf {x} _{i}}$ 여기서$$ $\phi {\displaystyle \mathrm{}}$: ${\displaystyle {}^{}}$ d${\displaystyle {}^{}}$→ R ${\displaystyle {}^{}}$ ${\$ $\},$ .

점을 임의의 클러스터로 나누는 하이퍼플레인 구축이 용이하다.물론 이 $\phi {\displaystyle \mathrm{}}$ ${\displaystyle \Phi }$은(는) 선형 독립$$ 벡터를 생성하므로 선형 PCA에서처럼 명시적으로 eigendecomposition을 수행할 공분산은 없다.

그 대신 커널 PCA에서 비독점적이고 임의적인 ${\displaystyle \Phi}$ 함수는$$ 명시적으로 계산되지 않는 '초센'으로, 만약 우리가 그 공간에서 실제로 데이터를 평가할 필요가 없다면 매우 고차원 ${\displaystyle \Phi$s를 사용할 수 있다.우리는 일반적으로 $\phi {\displaystyle \mathrm{}}$ ${\displaystyle \Phi }$ -space에서$$ 일하는 것을 피하려고 하기 때문에, 우리는 N-by-N 커널을 만들 수 있다.

${\displaystyle K=k(\mathbf {x},\mathbf {y})=(\Phi(\mathbf {x}),\Phi(\mathbf {y} )=\Phi(\mathbf {x} )^{{{}T}\Phi(\mathbf {y} )}$

다른 난해한 형상 공간의 내부 제품 공간(Gramian matrix 참조)을 나타낸다.커널 생성에서 발생하는 이중 형태는 ${\displaystyle a\mathbf{}}$ (x ) ${\displaystyle \Phi (\mathbf {x})}$ -space$$ (커널 트릭 참조)에서 공분산 행렬의 고유 벡터와 고유값을 실제로 결코 실제로 해결하지 못하는 PCA 버전을 수학적으로 공식화할 수 있게 해준다.K의 각 열에 있는 N 요소는 모든 변환된 점(N점)에 대해 변환된 데이터의 한 점의 점 산물을 나타낸다.몇몇 잘 알려진 커널은 아래 예에 나와 있다.

우리는 피쳐 공간에서 직접 작업하지 않기 때문에 PCA의 커널 형성은 PCA가 주성분 그 자체가 아니라 그 요소들에 대한 우리의 데이터의 투영법을 계산한다는 점에서 제한된다.형상 공간 $\phi {\displaystyle \mathrm{}(x\mathbf{}}$) ${\displaystyle \Phi(\mathbf {x})$의 한 지점에서 ${\displaystyle {k번째}^{}}$ 주성분 $V{\displaystyle {}^{}}$ k ${\$ V$^{k}}$에 대한$$ 투영을 평가하려면($$여기서 상위첨자 k는 k의 전원이 아닌 성분 k를 의미한다)

${\displaystyle {\mathbf {V}^{k}}^{{}}}T}\Phi(\mathbf {x} )=\왼쪽(\sum _{i=1}^{N}\mathbf {a_{i}}^{k}\Phi(\mathbf {x_{i}} )\오른쪽)^{T}\Phi(\mathbf {x} )}$

We note that ${\displaystyle \Phi (\mathbf {x_{i}} )^{T}\Phi (\mathbf {x} )}$ denotes dot product, which is simply the elements of the kernel ${\displaystyle K}$. It seems all that's left is to calculate and normalize the ${\displaystyle \mathbf {a_{i}} ^{k}}$, which can be done by 고유벡터 방정식 해결

${\displaystyle N\lambda \mathbf {a} =K\mathbf {a}}$

여기서 N은 집합의 데이터 포인트 수이고, $\lambda {\displaystyle }$ ${\displaystyle \lambda }$과($와{\displaystyle \mathbf{}}$) ${\$a} {a$}$은$($는) $K{\displaystyle }$ ${\$의 고유값 및 고유 벡터입니다$.$ 그런 다음, 고유 벡터를 정규화하려면 k {$k$을 정규화하십시오.

${\displaystyle 1=(\mathbf {V}^{k})^{{}^{{}}}T}\mathbf {V} ^{k}}}$

$x{\displaystyle }$ ${\displaystyle x}$의 원래 공간에 0-평균이 있든 없든 피쳐 공간(우리는 명시적으로 계산하지 않는다)의 중심이 되는 것이 보장되지 않는다는 사실에 주의해야 한다.효율적인 주성분 분석을 수행하려면 중심 데이터가 필요하므로 $K{\displaystyle }$ ${\displaystyle K}$을(를) '중앙집중화'$하여$ K${\displaystyle {}^{}}${$${\$displaystyle K'$가 된다.

${\displaystyle K'=K-\mathbf {1_{N}K-K\mathbf {1_{N} +\mathbf {1_{N}K\mathbf {1_{N}}}}}}}$

여기서 ${\displaystyle {1N\mathbf{}}_{}}$ ${\${${\displaystyle 1\_}$${N}}}$은(는) 각 요소가 $값{\displaystyle \mathrm{}}$ 1${\displaystyle }$/ N ${\displaystyle 1/N}$을(를) 취하는 N-by-N 매트릭스를$$ 의미한다$.$ 위에서 설명한 커널 PCA 알고리즘을 수행하기 $위해$ K${\displaystyle {}^{}}$′ ${\$을 사용한다.

커널 PCA에 대한 한 가지 주의사항이 여기에 설명되어야 한다.선형 PCA에서는 고유값을 사용하여 각 주성분에 의해 수집되는 데이터의 변동량을 기준으로 고유 벡터의 순위를 매길 수 있다.이는 데이터 차원성 감소에 유용하며 KPCA에도 적용될 수 있다.그러나 실제로 데이터의 모든 변형이 동일한 경우가 있다.이것은 일반적으로 커널 스케일의 잘못된 선택에 의해 발생한다.

대규모 데이터셋

실제로 큰 데이터 세트는 큰 K로 이어지고, K를 저장하는 것이 문제가 될 수 있다.이를 처리하는 한 가지 방법은 데이터 집합에서 클러스터링을 수행하고 커널을 클러스터링의 수단으로 채우는 것이다.이 방법이라도 비교적 큰 K를 산출할 수 있기 때문에, 고유값의 상위 P 고유값과 고유값의 고유 벡터만 이런 식으로 계산하는 것이 일반적이다.

예

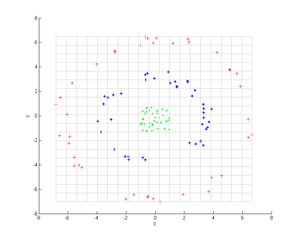
세 개의 동심원형 점 구름(표시)을 고려하십시오. 우리는 커널 PCA를 사용하여 이러한 그룹을 식별하고자 한다.점의 색상은 알고리즘에 관련된 정보를 나타내지 않고 변환이 데이터 점의 위치를 다시 지정하는 방법만 보여준다.

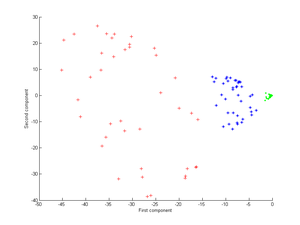
첫째, 커널을 고려하라.

${\displaystyle k({\boldsymbol {x},{\boldsymbol {y})=({\boldsymbol {x}^{\boldsymbol {T}}{\boldsymbol {y}+1)^{2}}$

이것을 커널 PCA에 적용하면 다음 이미지가 생성된다.

이제 가우스 커널을 고려하십시오.

${\displaystyle k({\boldsymbol{x},{\\boldsymbol{y}}=e^{\frac {-}-{\{symbol {x}-{2}}\{2\sigma ^{2}}},}$

즉, 이 커널은 폐쇄성의 척도로, 점이 일치할 때 1과 같고 무한에서 0과 같다.

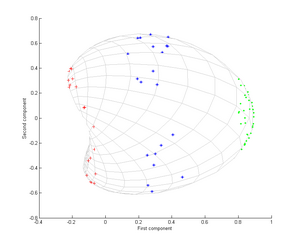
특히, 선형 PCA는 이러한 동심점 구름이 선형적으로 분리할 수 없는 주어진 (이 경우 2차원) 공간에서만 작동하기 때문에 선형 PCA만을 사용하여 불가능한 세 개의 다른 그룹을 구별하기에 충분하다는 점에 유의한다.

적용들

커널 PCA는 새로움 감지^[3] 및 이미지 디노이즈에 유용한 것으로 입증되었다.^[4]

참고 항목

• 군집 분석
• 비선형 차원성 감소
• 스펙트럼 클러스터링

참조