그레이엄 스캔

그레이엄의 스캔은 시간 복잡성이 O(n log n)인 평면에서 유한한 점 집합의 볼록 선체를 찾는 방법이다. 1972년 원래의 알고리즘을 발표한 로널드 그레이엄의 이름을 따서 지은 것이다.^[1] 이 알고리즘은 경계를 따라 정렬된 볼록 선체의 모든 정점을 찾아낸다. 그것은 효율적으로 경계의 결점을 감지하고 제거하기 위해 스택을 사용한다.

알고리즘.

이 알고리즘의 첫 번째 단계는 가장 낮은 y 좌표로 점을 찾는 것이다. 집합에서 가장 낮은 y 좌표가 한 점 이상 존재하는 경우 후보 중에서 가장 낮은 x 좌표가 있는 점을 선택해야 한다. 이 점을 P라고 불러라. 이 단계에서는 O(n)를 사용하며 여기서 n은 문제의 포인트 수입니다.

다음으로 포인트 세트는 X축으로 포인트 P가 만드는 각도 및 포인트의 증가 순서로 정렬해야 한다. 예를 들어 Hapsort(O(n log n))와 같은 범용 정렬 알고리즘이 이에 적합하다.

각도 순서대로 정렬하는 것은 각도를 계산할 필요가 없다. $[{\displaystyle }$ ${\displaystyle 0,}$ ${\displaystyle \pi }$ ${\displaystyle ]}$ $[\displaystyle [0,\pi ]}$ 간격에서 단조로운 각도의 모든 기능을 사용할 수 있다.$$ 코사인(cosine)은 도트 제품을 사용하여 쉽게 계산하거나 선의 기울기를 사용할 수 있다. 숫자 정밀도가 위태로운 경우, 정렬 알고리즘에 의해 사용되는 비교 함수는 교차 제품의 기호를 사용하여 상대 각도를 결정할 수 있다.

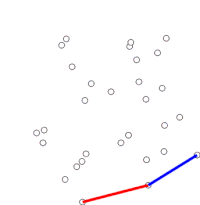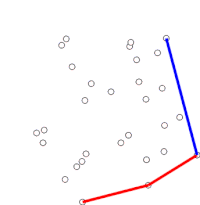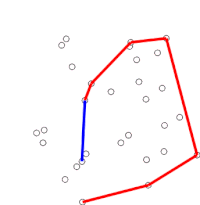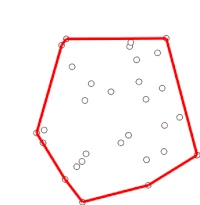
알고리즘은 정렬된 배열의 각 점을 순차적으로 고려하여 진행한다. 각 점에 대해, 이 지점 바로 앞의 두 지점에서 이동하는 것이 좌회전인지 우회전을 하는지에 해당하는지 먼저 판단된다. 우회전하면 2~마지막 지점이 볼록한 선체의 일부가 아니고 '내부'에 놓여 있다. 그런 다음 선체 내부에 있었던 것으로 밝혀진 지점 바로 앞에 있는 지점과 두 지점의 집합에 대해 동일한 결정을 내리고, "좌회전" 세트가 마주칠 때까지 반복하며, 이때 알고리즘이 정렬된 배열의 점 집합에서 발견된 어떤 지점도 뺀 다음 지점으로 이동한다. 선체 내부; 이 점들을 다시 고려할 필요가 없다. (어느 단계에서든 세 지점이 시준될 경우, 어떤 용도에서는 볼록한 선체 경계에서 모든 지점을 찾아야 하기 때문에 폐기 또는 보고 중 하나를 선택할 수 있다.)

다시 말하지만, 세 점이 "좌회전" 또는 "우회전"을 구성하는지를 결정하는 것은 두 선 세그먼트 사이의 실제 각도를 계산할 필요가 없으며, 실제로 단순한 산술만으로 달성할 수 있다. For three points ${\displaystyle P_{1}=(x_{1},y_{1})}$, ${\displaystyle P_{2}=(x_{2},y_{2})}$ and ${\displaystyle P_{3}=(x_{3},y_{3})}$, compute the z-coordinate of the cross product of the two vectors ${\d$$isplaystyle {\overrightarrow {P_{1}P_{2}}}}$ and ${\displaystyle {\overrightarrow {P_{1}P_{3}}}}$, which is given by the expression ${\displaystyle (x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})}$. If the result is 0점들은 일직선으로 표시되며, 양수일 경우 세 점은 "좌회전" 또는 시계 반대 방향, 그렇지 않을 경우 "우회전" 또는 시계 반대 방향(시계 반대 방향의 경우)을 구성한다.

이 과정은 결국 알고리즘이 완성되고 이제 스택이 시계 반대 방향으로 볼록 선체에 있는 지점을 포함하는 그것이 시작된 지점으로 되돌아간다.

시간 복잡성

점을 정렬하면 시간 복잡성이 O(n log n)이다. 루프의 시간 복잡성은 O(n²)로 보일 수 있지만, 각 포인트에 대해 이전 포인트 중 하나가 "우회전"을 하는지 확인하기 위해 되돌아 가기 때문에, 각 포인트는 어떤 의미에서는 최대 2배까지 고려되기 때문에 사실상 O(n)이다. Each point can appear only once as a point ${\displaystyle (x_{2},y_{2})}$ in a "left turn" (because the algorithm advances to the next point ${\displaystyle (x_{3},y_{3})}$ after that), and as a point ${\displaystyle (x_{2},y_{2})}$ in a "right turn" (because the 점$({\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}}$y ${\displaystyle {2\mathrm{}}_{}}$) ${\displaystyle(x_{2},y_{2}})$이(가) 제거됨$$). 따라서 정렬 시간이 볼록한 선체를 실제로 계산하는 시간을 지배하기 때문에 전체적인 시간 복잡성은 O(n log n)이다.

가성음

이 코드 아래, 시계 방향으로 만약ccw<00. 만약 3점, collinear 정 방향으로 턴을 하다 기능 ccw:ccw>를 사용한다면 ccw=0.(에서 실제 적용에, 만약 그 좌표 임의의 실수를, 그 기능을 필요로 한다 정확한 비교의 부동 소수 점 숫자 및 사람에 조심하라 숫자 특이점에"거의"collinear.지점s.)

그런 다음 결과를 에 저장하십시오. stack.

점들을 스택의 목록으로 설정 = empty_stack()은 P0과 극각으로 P0 정렬 지점이라고 불리는 가장 낮은 y-좌표와 가장 왼쪽 점을 찾는다. 여러 점이 동일한 극각인 경우 점의 가장 먼 거리를 유지한다: # 만약 우리가 시계방향으로 회전하여 이 지점에 도달하면 스택에서 마지막 점을 표시한다.k > 1과 ccw(다음_to_top(스택), 상단(스택), 포인트 <= 0: 팝 스택 푸시포인트 to 스택 엔드) 

이제 스택에는 볼록한 선체가 들어 있는데, 그 선체는 점들이 시계 반대 방향으로 향하며 P0이 첫 번째 지점이다.

여기, next_to_top() 스택을 변경하지 않고 스택 상단 아래 항목 1개를 반환하는 기능이며, 이와 유사하게, top() 최상위 요소 반환용.

이 유사코드는 도입에서 알고리즘으로 수정되었다.

메모들

입력을 각도 대신 x좌표로 분류하고 선체를 2단계로 계산해 각각 선체의 상부와 하부를 생산하면 같은 기본 아이디어도 작동한다. 이 수정은 A. M. 앤드류가^[2] 고안했으며 앤드류의 모노톤 체인 알고리즘으로 알려져 있다. 그것은 그레이엄의 스캔과 동일한 기본 특성을 가지고 있다.^[3]

그레이엄의 스캔에 사용된 스택 기법은 가장 가까운 모든 작은 값 문제에 대해 그것과 매우 유사하며, 모든 가장 가까운 작은 값에 대한 병렬 알고리즘도 점의 정렬된 시퀀스의 볼록한 선체를 효율적으로 계산하기 위해 (그레이엄의 스캔과 같이) 사용될 수 있다.^[4]

수치 강건성

수치 건전성은 유한정밀 부동소수점 컴퓨터 산수를 사용하는 알고리즘에서 다루어야 할 문제다. 2004년 논문은 특히 Graham 스캔의 구현에 사용할 수 있는 단순한 증분 전략을 분석했다.^[5] 논문의 명시적 목표는 알고리즘을 구체적으로 분석하는 것이 아니라, 연산 기하학에서 부동소수점 계산으로 인해 무엇이 어떻게 실패할 수 있는지 교과서적인 예를 제공하는 것이었다.^[5] 나중 D. 장과 N.F. Stewart는^[6] 이것에 대해 상세히 설명했고 후진적 오류 분석을 사용하여 두 가지 주요한 결론을 내렸다. 첫 번째는 볼록한 선체가 잘 갖춰진 문제여서 합리적인 오차범위 내에서 답을 내는 알고리즘을 기대할 수 있다는 점이다. 둘째, 그들은 Graham-Fortune이라고 부르는 Graham 스캔의 수정(숫자 안정성을^[7] 위해 Steven Fortune의 아이디어를 통합)이 유한 정밀도와 부정확한 데이터의 문제를 "가능한 범위까지" 극복한다는 것을 증명한다.

참고 항목

• 볼록 선체 알고리즘

참조

추가 읽기

• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "33.3: Finding the convex hull". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 949–955. ISBN 0-262-03293-7.