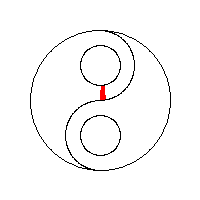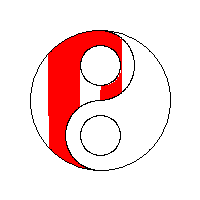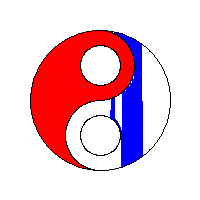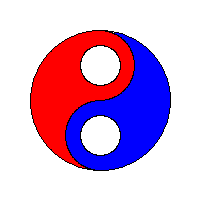
플래드필
Flood fillFlood Fill(시드 필이라고도 함)은 일치하는 속성을 가진 다차원 배열의 특정 노드에 연결된 영역을 결정하고 변경하는 플래딩 알고리즘입니다.페인트 프로그램의 "버킷" 채우기 도구에서 서로 연결된 유사한 색상의 영역을 다른 색으로 채우거나 Go 및 지뢰 찾기 같은 게임에서 제거된 조각을 결정하기 위해 사용됩니다.경계 채우기라고 하는 배리언트는 같은 알고리즘을 사용하지만 특정 속성이 [1]없는 특정 노드에 연결된 영역으로 정의됩니다.
플래드 필링은 채워진 폴리곤을 그리는데 적합하지 않습니다.더 날카로운 모서리에서 일부 픽셀을 놓치기 때문입니다.[2] 대신 짝수 규칙과 0이 아닌 규칙을 참조하십시오.
알고리즘 파라미터
기존의 플래드필 알고리즘에는 시작 노드, 타깃 색상 및 대체 색상의 3가지 파라미터가 있습니다.이 알고리즘은 대상 색상의 경로에 의해 시작 노드에 연결된 배열 내의 모든 노드를 검색하여 대체 색상으로 변경합니다.경계 채우기의 경우 대상 색상 대신 경계 색상이 제공됩니다.
일반적인 방법으로 알고리즘을 일반화하기 위해 다음 설명에서는 대신 두 가지 루틴을 사용할 수 있습니다.[3] 한 명이 전화했어요Inside채우지 않은 포인트에 대해 색상별로 채운 영역 안에 있는 경우 true를 반환하고, 그 중 하나가 호출됩니다.Set픽셀/노드를 채웁니다.다음 중 하나를 가진 노드Set그러면 더 이상 요구되어서는 안 된다.Inside.
노드가 연결된 모서리에 접촉하는지 여부에 따라 각각 8방향과 4방향의 두 가지 종류가 있습니다.
스택 기반 재귀 구현(4방향)
가장 먼저 알려진 암묵적인 스택베이스, 재귀, 4방향 플래드필 실장은 다음과 같습니다.[4][5][6][7]
Flood-fill(노드): 1. 노드가 Inside return이 아닌 경우 2. 노드 3을 설정합니다.노드 남쪽으로 한 단계 Flood-fill을 수행합니다. 4. 노드 5의 북쪽으로 한 단계 Flood-fill을 수행합니다.노드 6의 서쪽으로 Flood-fill을 실행하고 노드7의 동쪽으로 Flood-fill을 실행합니다.돌아가다.
상기의 알고리즘의 실장은 이해하기 쉽지만, 스택 스페이스가 매우 제약되어 있는 언어나 환경(마이크로 컨트롤러 등)에서는 실용적이지 않습니다.
데이터 구조로 재귀 이동
재귀를 데이터 구조(스택 또는 큐)로 이동하면 스택 오버플로를 방지할 수 있습니다.단순한 재귀적 솔루션과 비슷하지만 재귀적 콜을 실행하는 대신 스택 또는 큐에 노드를 푸시하여 소비합니다.데이터 구조의 선택은 확산 패턴에 영향을 줍니다.
플래드필(노드): 1Q를 빈 큐 또는 스택으로 설정합니다.2 .Q.3의 끝에 노드를 추가합니다.Q가 비어 있지 않은 동안: 4.n을 Q. 5의 첫 번째 요소와 동일하게 설정합니다. Q. 6에서 첫 번째 요소를 제거합니다. n이 Inside인 경우:n 노드를 n의 서쪽에 Q의 끝에 추가합니다.n의 동쪽에 있는 노드를 Q의 끝에 추가합니다.n의 북쪽에 있는 노드를 Q의 끝에 추가합니다.n의 남쪽에 있는 노드를 Q.7의 끝에 추가합니다.Q가 소진될 때까지 루프를 계속합니다.8. 되돌아가다.
한층 더 잠재적인 최적화
- 스택/큐에 추가하기 전에 각 노드의 픽셀 색상을 확인하고 설정하여 스택/큐 크기를 줄입니다.
- 이동 시 위/아래 픽셀을 큐잉하여 동쪽/서쪽 방향에 루프를 사용합니다(아래의 스팬 채우기 알고리즘과 유사).
- 순서가 다른 프로세서를 병렬화할 수 있도록 하기 위해 추가 스택/큐와 함께 코드의 복사본을 2개 이상 남겨둡니다.
- 여러 스레드를 사용합니다(이상적으로는 방문 주문이 약간 다르므로 같은 [6]영역에 머무르지 않습니다).
이점
- 매우 심플한 알고리즘 - 버그 없이 쉽게 만들 수 있습니다.[6]
단점들
- 특히 스택을 사용할 때 많은 메모리를 사용합니다.[6]
- 가장 꽉 찬 픽셀을 총 4회 테스트합니다.
- 픽셀 테스트 결과를 변경해야 하므로 패턴 채우기에 적합하지 않습니다.
- 큐잉 배리언트에서는 접근패턴이 캐시에 친화적이지 않습니다.
- 멀티픽셀 워드 또는 비트플레인에 쉽게 최적화할 수 없습니다.[2]
스팬 충전
주로 스팬을 사용하여 작업함으로써 상황을 더욱 최적화할 수 있습니다.처음 공개된 완전한 예는 다음과 같은 기본 원칙에 따라 작동합니다.[1] 시드 포인트부터 시작하여 왼쪽과 오른쪽을 채우고 가장자리를 추적합니다.그런 다음 위의 줄과 아래의 줄을 동일한 부분으로 스캔하여 계속할 새 시드 포인트를 검색합니다.이 알고리즘은 가장 많이 채워진 픽셀을 총 3회 테스트했음에도 불구하고 인용과 구현[citation needed] 모두에서 가장 많이 사용됩니다.의사 코드 형식:
fn fill(x, y): Inside(x, y)가 아닌 경우 s = s에 새 빈 스택 또는 큐 추가(x, y)를 반환합니다. s let lx = x while Inside(lx - 1, y): Set(lx - 1, y) lx - 1 while Y(x inside): Set(lx - 1, y)s) fn scan(lx, rx, y, s): lx의 x에 대해 = false를 추가합니다.rx: Inside(x, y): 추가됨 = 추가되지 않은 경우 false:s에 추가(x, y) = 참
시간이 지남에 따라 다음과 같은 최적화가 실현되었습니다.
- 새 스캔이 완전히 조부모님 범위 내에 있을 경우 채워진 픽셀만 찾을 수 있으므로 대기열에 넣을 필요가 없습니다.[1][6][3]
- 또, 새로운 스캔이 조부모의 스팬에 겹치는 경우는, 오버행(U턴, W턴)만을 스캔 하면 됩니다.[3]
- 시드를 스캔하는 동안 채울 수 있습니다.
그리고 1990년에 최종 복합 스캔 앤 필 스판 필러가 발표되었습니다.의사 코드 형식:
Fnfill(), y):독자 Inside(), y) 다음 돌아온다 바로 그런 새로운 빈 큐나 스택 =는 동안 s 비어 있는 것이 아니가 어떻게 되가 어떻게 될(x, 음, y-1, 음)추가(x, x, y, 1)추가:s에서(x1, 미국, y, dy)을 제거합시다 x)x1 만약 Inside(), y):Inside(x-1, y):Set(x-1, y)))x-1만약 x의<>x1:(), x1-1, y-dy, -d을 넣으세요.y)x1 <= x2: while Inside(x1, y): Set(x1, y): x1 = x1 + 1 Add(x, x1 - 1, y+dy, dy)를 s if x1 - 1 > x2에 추가(x2 + 1, x1 - 1, x1 - 1, y-dy, dy)
이점
단점들
- 이미 채워진 픽셀을 계속 방문합니다(일반적인 알고리즘의 경우 대부분의 픽셀을 3회 스캔합니다).마지막으로, 채워진 영역에 구멍이 있는 픽셀만 추가로 스캔합니다.)[3]
- 픽셀 테스트 결과를 변경해야 하므로 패턴 채우기에 적합하지 않습니다.
패턴 채우기 지원 추가
스판 및 픽셀 기반 알고리즘이 패턴 채우기를 지원하도록 하는 두 가지 일반적인 방법은 플레인 채우기로서 고유한 색상을 사용한 후 패턴으로 대체하거나, 방문한 픽셀을 추적(2d 부울 배열 또는 영역)하여 픽셀 채우기가 불가능함을 나타내는 것입니다.그런 다음 Inside는 방문한 픽셀에 대해 false를 반환해야 합니다.[3]
그래프 이론 충전
일부 이론가들은 명시적인 그래프 이론을 문제에 적용하여 픽셀의 범위 또는 그러한 집합의 범위를 노드와 같이 처리하고 그 연결성을 연구했습니다.처음 공개된 그래프 이론 알고리즘은 위의 스팬 필링과 유사하게 작동했지만 스팬 필링이 중복되는 시기를 검출하는 방법이 있었다.[9] 안타깝게도 일부 충전을 완료하지 못하는 버그가 있었습니다.[10] 수정된 알고리즘은 나중에 그래프 이론에서 유사한 근거를 가지고 출판되었습니다. 그러나, 그것은 진행에 따라 이미지를 변화시켜 잠재적인 루프를 일시적으로 차단하고 프로그래밍 인터페이스를 복잡하게 만듭니다.[10]나중에 공개된 알고리즘은 경계가 이미지 내의 다른 모든 것과 구별되는 것에 의존하기 때문에 대부분의 용도로는 적합하지 않습니다.또한 부기를 위해서는 픽셀당 추가 비트가 필요합니다.[3]
이점
- 채워진 픽셀을 다시 테스트하지 않기 때문에 직접 패턴 채우기에 적합합니다.[9] [10] [11]
- 복잡하지 않은 채우기를 위해 원래 스판 알고리즘의 속도를 두 배로 높입니다.[3]
- 액세스 패턴은 캐시로 비트플레인에 적합합니다.[6][3]
단점들
- 정기적으로 스팬을 큐의 다른 모든 '전면'과 비교해야 하므로 복잡한 채우기가 현저하게 느려집니다.[3]
- 그래프 이론 도메인과 픽셀 도메인 사이를 왔다 갔다 하면 이해가 복잡해집니다.
- 이 코드는 상당히 복잡하기 때문에 버그가 발생할 가능성이 높아집니다.
워크 베이스 충전(고정 메모리 방식)
궁지에 몰리지 않고 그림을 그리려는 화가인 것처럼 꾸며 4개의 연결된 영역에 대한 기억을 근본적으로 사용하지 않는 방법이 존재한다.이것도 미로를 푸는 방법이에요.기본 경계를 이루는 4개의 픽셀을 검사하여 어떤 조치를 취해야 하는지 확인합니다.화가는 다음과 같은 몇 가지 상황 중 하나에 처할 수 있었다.
- 네 개의 경계 픽셀이 모두 채워집니다.
- 경계 픽셀 중 3개가 채워집니다.
- 경계 화소 중 2개가 채워진다.
- 경계 픽셀 하나가 채워집니다.
- 0 경계 픽셀이 채워집니다.
경로 또는 경계를 따르는 경우 오른쪽 규칙이 사용됩니다.화가는 오른손을 벽(지역 경계)에 대고 손을 떼지 않고 지역 가장자리를 따라 나아갑니다.
케이스 #1의 경우, 화가가 서 있는 픽셀을 도장(필링)하고 알고리즘을 정지합니다.
케이스 #2의 경우 영역 밖으로 이어지는 경로가 존재합니다.화가가 서 있는 픽셀을 그리고 열린 경로 방향으로 이동합니다.
케이스 #3의 경우, 2개의 경계 픽셀은 현재 픽셀을 칠하면 경로의 반대편으로 돌아가는 것을 차단할 수 있는 경로를 정의합니다.정확히 같은 픽셀로 돌아갈 수 있는지 확인하기 위해 현재 위치와 방향을 정의하기 위해 "표시"가 필요합니다.이러한 「마크」를 이미 작성했을 경우는, 이전의 마크를 보존하고, 오른쪽의 룰에 따라서 다음의 픽셀로 이동합니다.
처음 발견된 2픽셀 경계에 마크를 사용하여 통로가 어디서 시작되었고 화가가 어떤 방향으로 이동했는지 기억합니다.만약 마크가 다시 발견되고 화가가 같은 방향으로 이동한다면, 마크가 있는 사각형을 그리고 같은 방향으로 계속 가는 것이 안전하다는 것을 화가는 알게 된다.그 이유는 (알 수 없는 경로를 통해) 나중에 마크의 다른 쪽에 있는 픽셀에 도달하여 칠할 수 있기 때문입니다.나중에 사용할 수 있도록 마크를 제거합니다.
만약 화가가 표식과 마주쳤지만 다른 방향으로 가고 있다면, 일종의 루프가 발생하고, 그것이 화가가 표식으로 되돌아가는 원인이 된 것입니다.이 루프는 삭제해야 합니다.마크를 집어들고, 화가는 왼쪽의 경계선(오른쪽의 줄과 비슷하지만 화가의 왼손을 사용)을 사용하여 앞서 표시한 방향으로 나아간다.이 작업은 교차로(3개 이상의 열린 경계 픽셀)가 발견될 때까지 계속됩니다.왼쪽 규칙을 사용하여 이제 화가는 단순한 통로(두 개의 경계 픽셀로 만든)를 검색합니다.이 2픽셀 경계 경로를 찾으면 해당 픽셀이 그려집니다.이것에 의해, 루프가 끊어지고 알고리즘이 속행됩니다.
케이스 #4의 경우 반대쪽 8개의 연결된 모서리가 채워져 있는지 확인해야 합니다.둘 중 하나 또는 둘 다 채워지면 다중 경로 교차로가 생성되어 채울 수 없습니다.둘 다 비어 있는 경우 현재 픽셀을 칠하고 오른쪽 규칙에 따라 화가를 이동할 수 있습니다.
알고리즘은 메모리와 시간을 교환합니다.단순한 형태일 경우 매우 효율적입니다.단, 형상이 복잡하고 많은 피쳐가 있는 경우 알고리즘은 영역의 가장자리를 추적하는 데 많은 시간을 소비하여 모든 것을 그릴 수 있도록 합니다.
이 알고리즘은 1981년 Vicom Systems, Inc.[citation needed]에 의해 제조된 Vicom 이미지 처리 시스템에서 상용화되었습니다.걷기 알고리즘은 [12]1994년에 발표되었다.전형적인 재귀 플래드필 알고리즘은 Vicom 시스템에서도 사용할 수 있었습니다.
유사 코드
다음으로 구조화된 영어로 기술된 최적의 고정 메모리플래드필 알고리즘의 의사 코드의 실장을 나타냅니다.
- 변수
cur,mark,그리고.mark2각각 픽셀 좌표 또는 null 값을 유지합니다.- 주의: 언제
marknull로 설정되었습니다. 이전 좌표 값을 지우지 마십시오.필요한 경우 해당 좌표를 호출할 수 있도록 유지합니다.
- 주의: 언제
cur-dir,mark-dir,그리고.mark2-dir각각 방향을 잡고 있다(왼쪽, 오른쪽, 위 또는 아래)backtrack그리고.findloop각각 부울값 보유count정수입니다.
- 알고리즘
- 주의: 모든 방향(전면, 후면, 왼쪽, 오른쪽)은
cur-dir
cur를 시작 픽셀로 설정하고 cur-dir를 기본 방향 클리어 마크로 설정하며 mark2(값을 null로 설정)를 사용하여 전면 픽셀이 비어 있는 동안 백트랙 및 파인드 루프를 false로 설정합니다. START MAIN LOUP로 점프하는 동안 앞으로 이동: 오른쪽 픽셀이 내부에 있으면 백트랙이 false이고 find 루프가 false이면 앞으로 이동합니다.el은 안쪽에서 오른쪽으로 돌면 findloop을 true end로 설정합니다. START: 카운트가 4가 아닌 경우 카운트를 채워진 비다각형 인접 픽셀의 수(앞/뒤/왼/오른쪽만 해당)로 설정합니다.앞쪽 픽셀이 안쪽일 때 오른쪽으로 돌면 왼쪽으로 돌립니다.스위치 카운트 케이스1이 true인 경우 front-loop이 inside end가 아닌 경우 findloop을 true로 설정하고 findloop이 true인 경우 마크가 null인 경우 front-left-loop과 back-left-loop이 모두 inside인 경우 마크가 종료됩니다.백픽셀이 내부에 없는 경우 엔드 케이스 2의 경우 Cur 점프를 PAINT end로 설정 해제하고, 전면 왼쪽 픽셀이 내부에 있는 경우 PAINT end로 설정한다. 그렇지 않은 경우 마크가 설정되지 않은 경우 Cur 점프를 PAINT end로 설정한다.mark를 cur로 set mark-set to cur-seclear mark2로 set mark-set findloop, mark2가 설정되지 않은 경우 false로 설정합니다.cur-set cur-set cur가 마크와 같으면 clear mark가 반전됩니다.cur jump를 PAINT로 설정합니다.그렇지 않으면 findloop이 true이면 false findloop을 mark-dir end로 설정하고 mark2를 cur로 설정합니다.cur가 마크에 있는 경우 mark2-turn을 cur-turn end로 설정하고, cur가 마크2-turn clear mark2를 마크2-turn around set cur2를 마크2로 설정한다.cur가 mark2에 있는 경우 마크를 cur-dir로, mark-dir를 mark2 end로 설정합니다(엔드 케이스 3 clear mark set cur jump t).o 페인트 엔드 케이스 4 세트 커 완료 엔드 케이스 엔드 스위치 엔드 메인 루프
이점
- 메모리 사용량이 일정합니다.
단점들
- 액세스 패턴이 캐시 또는 비트플레인에 적합하지 않습니다.
- 루프를 닫기 전에 많은 시간을 루프를 돌아다닐 수 있습니다.
벡터 실장
Inkscape 버전 0.46에는 버킷 채우기 툴이 포함되어 있어 통상의 비트맵 조작과 유사한 출력을 얻을 수 있습니다.실제로 캔버스가 렌더링되고 선택된 영역에서 플래드 채우기 조작이 실행되며 그 결과가 경로로 추적됩니다.경계 조건의 개념을 사용합니다.
「 」를 참조해 주세요.
외부 링크
레퍼런스
- ^ a b c Smith, Alvy Ray (1979). Tint Fill. SIGGRAPH '79: Proceedings of the 6th annual conference on Computer graphics and interactive techniques. pp. 276–283. doi:10.1145/800249.807456.
- ^ a b Ackland, Bryan D; Weste, Neil H (1981). The edge flag algorithm — A fill method for raster scan displays. IEEE Transactions on Computers (Volume: C-30, Issue: 1). pp. 41–48. doi:10.1109/TC.1981.6312155.
- ^ a b c d e f g h i j Fishkin, Kenneth P; Barsky, Brian A (1985). An Analysis and Algorithm for Filling Propagation. Computer-Generated Images: The State of the Art Proceedings of Graphics Interface ’85. pp. 56–76. doi:10.1007/978-4-431-68033-8_6.
- ^ Newman, William M; Sproull, Robert Fletcher (1979). Principles of Interactive Computer Graphics (2nd ed.). McGraw-Hill. p. 253. ISBN 978-0-07-046338-7.
- ^ Pavlidis, Theo (1982). Algorithms for Graphics and Image Processing. Springer-Verlag. p. 181. ISBN 978-3-642-93210-6.
- ^ a b c d e f g h i Levoy, Marc (1982). Area Flooding Algorithms. SIGGRAPH 1981 Two-Dimensional Computer Animation course notes.
- ^ Foley, J D; van Dam, A; Feiner, S K; Hughes, S K (1990). Computer Graphics: Principles and Practice (2nd ed.). Addison–Wesley. pp. 979–982. ISBN 978-0-201-84840-3.
- ^ Heckbert, Paul S (1990). "IV.10: A Seed Fill Algorithm". In Glassner, Andrew S (ed.). Graphics Gems. Academic Press. pp. 275–277. ISBN 0122861663.
- ^ a b Lieberman, Henry (1978). How to Color in a Coloring Book. SIGGRAPH '78: Proceedings of the 5th annual conference on Computer graphics and interactive techniques. pp. 111–116. doi:10.1145/800248.807380.
- ^ a b c Shani, Uri (1980). Filling regions in binary raster images: A graph-theoretic approach. SIGGRAPH '80: Proceedings of the 7th annual conference on Computer graphics and interactive techniques. pp. 321–327. doi:10.1145/800250.807511.
- ^ a b Pavlidis, Theo (1981). Contour Filling in Raster Graphics. SIGGRAPH '81: Proceedings of the 8th annual conference on Computer graphics and interactive techniques. pp. 29–36. doi:10.1145/800224.806786.
- ^ Henrich, Dominik (1994). Space-efficient region filling in raster graphics. The Visual Computer. pp. 205–215. doi:10.1007/BF01901287.