에레라 그래프
Errera graph| 에레라 그래프 | |
|---|---|
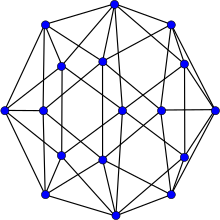 에레라 그래프 | |
| 이름을 따서 명명됨 | 알프레드 에레라 |
| 정점 | 17 |
| 가장자리 | 45 |
| 반지름 | 3 |
| 지름 | 4 |
| 둘레 | 3 |
| 자동형성 | 20(D10) |
| 색수 | 4 |
| 색도 지수 | 6 |
| 특성. | 플라나르 해밀턴어 |
| 그래프 및 모수 표 | |
그래프 이론의 수학적 분야에서 에레라 그래프는 17개의 정점과 45개의 가장자리를 가진 그래프다.알프레드 에레라는 1921년 4가지 색 정리에 대한 켐페의 잘못된 증거에 대한 반증으로서 이 책을 출판했다;[1][2] 그것은 허친슨 & 왜건 (1998년)에 의해 에레라의 이름을 따서 명명되었다.[1]
특성.
에레라 그래프는 평면이며 색도 번호 4, 색도 지수 6, 반지름 3, 지름 4, 둘레 3이 있다.모든 정점은 5도 또는 6도이며, 5Vertex 연결 그래프와 5Edge 연결 그래프다.
에레라 그래프는 정점-변환 그래프가 아니며 완전 자동형 집단은 순서가 20인 이음계 그룹, 회전과 반사를 모두 포함한 데카곤의 대칭 집단과 이형성이다.
The characteristic polynomial of the Errera graph is .
4색 정리 적용

네 가지 색 정리는 모든 평면 그래프의 정점을 네 가지 색으로 채색할 수 있으므로, 인접한 정점 두 개가 동일한 색상을 가지지 않도록 명시하고 있다.1879년 알프레드 켐페에 의해 잘못된 증거가 발표되었으나, 1890년에 이르러서 잘못된 것으로 밝혀졌다.4색 정리는 1976년까지 유효한 증거가 주어지지 않았다.켐페의 증명서는 평면 그래프를 색칠하는 알고리즘으로 번역될 수 있는데, 이것 또한 잘못된 것이다.1890년과 1896년 그의 증거에 대한 백작샘플이 발견되었고(푸신 그래프), 이후 프리치 그래프와 소이퍼 그래프는 두 개의 더 작은 백작샘플을 제공했다.[3]그러나, 에레라의 작업이 있기 전까지, 이 백반샘플들은 전체 컬러링 알고리즘이 실패한다는 것을 보여주지 못했다.오히려, 그들은 그래프의 꼭지점 하나를 제외한 모든 정점들이 이미 색칠되어 있다고 가정했고, 그러한 사전 예시된 예에서 켐페의 방법(그 방법을 전체 그래프에 확대하기 위해 색칠을 수정한다고 한다)이 실패했다는 것을 보여주었다.반면에 에레라 그래프는 켐페의 전체 방법에 대한 counterrexample을 제공한다.에레라 그래프에서 이 방법을 실행하면 정점이 없는 것부터 시작하여 전체 그래프에 대한 유효한 색상을 찾지 못할 수 있다.[1]또한 푸신 그래프와 달리 에레라 그래프의 모든 정점은 5도 이상이다.따라서 이 그래프에서 켐페의 방법에서 문제가 되는 경우는 낮은 수준의 정점을 선택함으로써 피할 수 없다.
이 그림은 이 그래프에서 켐페의 증명서가 어떻게 실패할 수 있는지를 보여주는 예를 보여준다.그림에서, 이 지도에서 지역 간의 보조성은 에레라 그래프를 형성하며, 부분적으로는 외부 지역이 무색인 4색이다.켐페의 잘못된 증거는 두 가지 색상만 가지고 있는 연결된 서브그래프인 켐페 체인을 기억함으로써 이것과 같은 부분적인 색상을 확장하려는 발상에 따른 것이다.그러한 사슬은 사슬의 모든 정점에 그것의 두 가지 색을 바꿈으로써 색상의 유효성을 보존하면서 기억될 수 있다.켐페의 증거는 색칠할 다음 꼭지점에 3개, 4개, 5개의 이웃이 있는지, 그리고 그 이웃들이 어떻게 색칠되는지에 따라 다른 경우를 가지고 있다.표시된 경우 다음에 색칠할 꼭지점은 지도 외부 영역에 해당하는 꼭지점이다.이 지역은 이미 네 가지 색깔의 이웃을 모두 가지고 있기 때문에 직접 색을 칠할 수 없다.파란색과 노란색 이웃은 단 하나의 켐페 체인으로 연결되어 있다(이미지의 파선 노란색 선에 의해 표시됨). 스왑이 그들을 파란색이나 노란색 둘 다로 만들지 못하게 하고 색깔을 자유롭게 한다.마찬가지로 파랑과 초록의 이웃들은 또 다른 켐페 체인(파선된 녹색 선)에 의해 연결되어 있다.그런 경우, 켐페의 증명서는 두 개의 켐페 체인, 즉 왼쪽의 적색-황색 체인, 오른쪽의 적색-녹색 체인(빨간색 선)에서 동시에 색상을 교환하려고 할 것이다.청록색 사슬은 왼쪽 적록색 사슬이 오른쪽 그래프에 닿는 것을 막고, 청록색 사슬은 오른쪽 적록색 사슬이 왼쪽으로 오는 것을 차단하기 때문에 이 두 사슬의 색을 동시에 교환하는 것은 안전한 작업인 것 같다.그러나 청황색과 청록색의 사슬은 떨어져 있기보다는 서로 교차하기 때문에, 적황색과 적녹색의 사슬이 만날 수 있는 지역이 있다.이 두 체인이 중간에서 만나면 동시 스왑은 이 중간 영역의 인접한 노란색과 녹색 정점(그림에서 위쪽 노란색과 녹색 영역으로 표현되는 정점 등)을 모두 빨간색으로 만들어 유효하지 않은 색상을 만들어낸다.
화학에서의 응용
화학 그래프 이론은 분자와 원자의 다른 군집의 그래프-이론적 구조에 관한 것이다.에레라 그래프 자체와 그 이중 그래프 모두 이 맥락에서 관련이 있다.
금과 같은 금속 원자는 중심 원자가 12개의 원자로 둘러싸인 군집을 형성할 수 있는데, 이 중 원자는 이코사슬론이다.또 다른, 더 큰 유형의 클러스터는 이러한 이두면체 군집들 중 두 개 군집을 합쳐서 형성될 수 있다. 그래서 각 군집의 중심 원자는 다른 군집의 경계 원자 중 하나가 된다.결과 19개 원자의 군집은 에레라 그래프의 패턴으로 외피에 17개의 원자가 있는 2개의 내부 원자(이코사헤드라의 중심)를 가지고 있다.[4]
에레라 그래프의 이중 그래프는 30개의 정점을 가진 풀러렌으로[1] 화학 문헌에 C(D305h)[5] 또는 F30(D5h)[6]로 지정되어 대칭을 나타내고 다른 30-Verex 풀러렌과 구별된다.이 모양은 또한 고차원 풀레네 건설에도 중심적인 역할을 한다.[6]
참조
- ^ a b c d Hutchinson, Joan; Wagon, Stan (1998), "Kempe revisited", American Mathematical Monthly, 105 (2): 170–174, doi:10.2307/2589650, JSTOR 2589650, MR 1605875.
- ^ Errera, A. (1921), Du coloriage des cartes et de quelques questions d'analysis situs, Ph.D. thesis.
- ^ Gethner, Ellen; Springer, William M., II (2003), "How false is Kempe's proof of the four color theorem?", Proceedings of the Thirty-Fourth Southeastern International Conference on Combinatorics, Graph Theory and Computing, Congressus Numerantium, 164: 159–175, MR 2050581.
- ^ Michael, D.; Mingos, P. (2015), "Structural and bonding patterns in gold clusters", Dalton Trans., 44 (15): 6680–6695, doi:10.1039/c5dt00253b, PMID 25710593.
- ^ Mathur, Rakesh Behari; Singh, Bhanu Pratap; Pande, Shailaja (2016), Carbon Nanomaterials: Synthesis, Structure, Properties and Applications, CRC Press, p. 59, ISBN 9781498702119.
- ^ a b Deza, Michel; Shtogrin, Mikhail (1999), "Three-, four-, and five-dimensional fullerenes", Southeast Asian Bulletin of Mathematics, 23 (1): 9–18, arXiv:math/9906035, Bibcode:1999math......6035D, MR 1810781.





