복합 프리즘

복합 프리즘은 여러 삼각형 프리즘 원소들이 서로 접촉하고, 서로 접합되어 단단한 조립체를 이루는 경우가 많다.^[1]여러 요소의 사용은 광학 설계자에게 다음과 같은 몇 가지 장점을 제공한다.^[2]

• 설계 파장에서 빔의 편차를 유발하지 않고 스펙트럼 분산을 달성할 수 있다.따라서 광축에 관해서 $angle$ ${\$ 각도로 들어가는 설계 파장의 빛은 같은 축에 관해서 프리즘을 같은 각도로 빠져나간다.이런 종류의 효과를 흔히 "직접 시력 분산" 또는 "비완화 분산"^[3]이라고 부른다.
• 입사 빔의 편차를 달성하는 동시에 빔에 유입되는 산포를 크게 줄일 수 있다: 무채색 편향 프리즘이다.이 효과는 빔 조향에 사용된다.^[4][5]
• 프리즘 산포를 조절하여 더 큰 산포 선형성을 얻거나 고차 산포 효과를 얻을 수 있다.

더블트

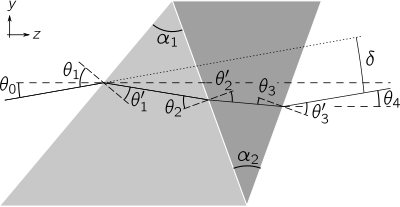
가장 단순한 복합 프리즘은 더블트(doublet)로, 오른쪽 그림에서 보듯이 접촉하는 두 원소로 구성되어 있다.프리즘을 통과하는 한 줄기 빛은 첫 번째 공기-유리 인터페이스에서 굴절되며, 다시 두 유리 사이의 인터페이스에서 굴절되며, 마지막 시간은 나가는 유리-공기 인터페이스에서 이루어진다.광선의$$ 편차각 ${\displaystyle \delta }$은(는) 입사 광선과 출구 광선 사이의 선각 차이에 의해 주어진다. $\Delta {\displaystyle }$= ${\displaystyle {0\mathrm{}}_{}}$ -${\displaystyle {}_{}{4\mathrm{}}_{}}$ 4 ${\$ 더블트 프리즘으로부터 직접적인 시력 분산을 생성할 수 있지만, 일반적으로 상당한 변위가 있다.빔(y 방향에서 두 점선 수평선 사이의 분리로서 표시됨).수학적으로 각 인터페이스에서 스넬의 법칙 방정식을 결합하여$$ $\Delta {\displaystyle }$ ${\displaystyle \delta }$을(를) 계산할 수 있다.^[2]

${\displaystyle{\begin{정렬}\theta _{1}&.=\theta _{0}-\beta _{1}&,\theta _{3}&.=\theta '_{2}-\alpha _{2}\\\theta '_{1}&, =\arcsin({\tfrac{1}{n_{1}}}\,\sin \theta_{1})\quad&\theta '_{3}&, =\arcsin(n_{2}\,\sin \theta_{3})\\\theta _{2}&amp을 말한다.=\theta '_{1}-\alpha _{1}&,\theta _{4}&.=\theta '_{3}+{\tfrac{1}{2}};=\arcsin({\tfrac{n_{1}}_{2}\\\theta '_{2}& \alpha.{n_{2}}:}\,\sin \theta _{2}\ended}}}$

편차 각도가 유리 굴절 ${\displaystyle {지수\mathrm{}}_{}}$ n 1 (${\displaystyle {}_{})}$ $){\displaystyle n_{1}(\dada$)과 ${\displaystyle n{}_{}}$2 ( $)){\displaystyle n_{2}(\dada$)의 비선형 함수로, 프리즘 요소의 꼭지각 $\alpha {\displaystyle {}_{}}$ ${\$$displaystystyle \{1}, α$ ${\displaystyle {2\mathrm{}}_{}}\{$1$},$ 발생$$ 각도${\displaystyle {\theta }_{}}$ ${\$${0}.$$\alpha {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 프리즘이 반전되었음을 나타낸다$$(첨부점 아래).

If the angle of incidence ${\displaystyle \theta _{0}}$ and prism apex angle ${\displaystyle \alpha }$ are both small, then ${\displaystyle \sin \theta \approx \theta }$ and ${\displaystyle {\text{arcsin}}(x)\approx x}$, so that the nonlinear equation in the deviation angle ${\$디스플레이 $스타일 \cHB }$은(는) 선형 형식으로 근사할 수 있음$$

${\displaystyle \property (\bigda )={\n_{1}-1}(\big ]}\big _{1}+{{{2}(\big ])-1\big [}\big [}\big ]\{2}\bigiteda }\.}$

(프리즘 편차 팬더 산포도 참조)더 나아가 굴절률에 대한 파장의 의존도가 대략 선형이라고 가정하면, 산포도는 다음과 같이 기록될 수 있다.

${\displaystyle \Delta ={\frac {\delta _{1}({\bar {\lambda }}}}{V_{1}}+{V_{\bar {\lambda }}}}}}},}$

where ${\displaystyle \delta _{i}}$ and ${\displaystyle V_{i}}$ are the dispersion and Abbe number of element ${\displaystyle i}$ within the compound prism, ${\displaystyle V_{i}=({\bar {n}}-1)/(n_{F}-n_{C})}$. The central wavelength of the spectrum is d에스코트된 $.{\$

doublet 프리즘은 종종 직접 시야 분산에 사용된다.그러한 프리즘을 설계하기 위해 ${\displaystyle \mathrm{\Delta }}$=${\displaystyle \stackrel{}{}}$0 ${\displaystyle {\bar {\delta }}=0}$을$($를) 두었고, 동시에 $\Delta {\displaystyle }${\$displaystyle \delta$}과$$ ${\displaystyle \Delta }$이(가$$)을(를)로 한다.

${\displaystyle \delta _{1}({\bar {\lambda }})=-\delta _{2}({\bar {\lambda }})=-\Delta {\Big (}{\frac {1}{V_{2}}}-{\frac {1}{V_{1}}}{\Big )}^{-1}\ ,}$

여기서 선택한 안경의 평균 굴절 지수에서$$ 원소의 에이펙스 각도 ${\displaystyle {\alpha \mathrm{}}_{}}$ 1 ${\$및$$ ${\displaystyle {\alpha \mathrm{}}_{}}$ 2 ${\$

${\displaystyle {\begin{aligned}\alpha _{1}&={\frac {\Delta }{{\bar {n}}_{1}-1}}{\Big (}{\frac {1}{V_{1}}}-{\frac {1}{V_{2}}}{\Big )}^{-1}\ ,\\\alpha _{2}&={\frac {\Delta }{{\bar {n}}_{2}-1}}{\Big (}{\frac {1}{V_{2}}}-{\frac {1}{V_{1}}}{\Big )}^{-1}\ .\end{aligned}}}$

이 공식은 작은 각도 근사치에서만 정확하다는 점에 유의하십시오.

더블아미치

더블트 프리즘이 가장 단순한 복합 프리즘 형태인 반면, 더블아미치 프리즘은 훨씬 더 흔하다.이 프리즘은 삼원계(삼원계)로, 제1원소와 제3원소가 같은 유리와 같은 정점 각도를 모두 공유하는 것이다.따라서 설계 레이아웃은 두 번째 요소의 중심을 통과하는 평면에 대칭이다.그것의 대칭성 때문에, 더블 아미치 프리즘에 대한 선형 설계 방정식(작은 각도 근사치 이하)은 각 방정식의 첫 번째 항 앞에 있는 2의 인수에 의해서만 더블트 프리즘의 그것과 다르다.^[2]

${\displaystyle {\begin{aligned}\delta ({\bar {\lambda }})&=2\delta _{1}({\bar {\lambda }})+\delta _{2}({\bar {\lambda }})=2{\big (}{\bar {n}}_{1}-1)\alpha _{1}+{\big (}{\bar {n}}_{2}-1)\alpha _{2}\ ,\\\Delta &=2{\frac {\delta _{1}({\bar {\lambda }})}{V_{1}}}+{\frac {\delta _{2}({\bar {\lambda }})}{V_{2}}}\ .\end{aligned}}}$

따라서, 우리는 이러한 선형 방정식을 사용하여 프리즘 각도에 대한 표현을 도출할 수 있으며,

${\displaystyle {\begin{aligned}\alpha _{1}&={\frac {\Delta }{2({\bar {n}}_{1}-1)}}{\Big (}{\frac {1}{V_{1}}}-{\frac {1}{V_{2}}}{\Big )}^{-1}\ ,\\\alpha _{2}&={\frac {\Delta }{{\bar {n}}_{2}-1}}{\Big (}{\frac {1}{V_{2}}}-{\frac {1}{V_{1}}}{\Big )}^{-1}\ .\end{aligned}}}$

편차 각도 $\Delta {\displaystyle }$ ${\displaystyle \delta }$에 대한 정확한 비선형 방정식은 각 인터페이스에서 얻은 굴절 방정식을 연결함으로써 얻는다$$.

${\displaystyle{\begin{정렬}\theta _{1}&.=\theta _{0}+\alpha _{1}-{\tfrac{1}{2}}\alpha _{2}&,\theta '_{3}&, =\arcsin({\tfrac{{2}}{n_{1}}}\,\sin \theta_{3n_})\\\theta '_{1}&, =\arcsin({\tfrac{1}{n_{1}}}\,\sin \theta_{1})\quad&\theta _{4}&amp을 말한다.=\theta '_{3}-\alpha _{1}\\\theta _{2}&.=\theta '_{1}-\alpha _{1}&,\theta '_{4}&, =\arcsin(n_{1}\,\sin \theta _{4}.)\\\theta '_{2}&=\arcsin({\tfrac {n_{1}}{n_{2}}}\,\sin \theta _{2})&\theta _{5}&=\theta '_{4}+\alpha _{1}-{\tfrac {1}{2}}\alpha _{2}\\\theta _{3}&=\theta '_{2}-\alpha _{2}\end{aligned}}}$

광선 편차 각도는 ${\displaystyle {\Delta \mathrm{}}_{}}$= ${\displaystyle {}_{}}$ 0 - ${\displaystyle {}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ ${\$ =\$theta _{0$}-\$theta$_${$5}}}로 주어진다.

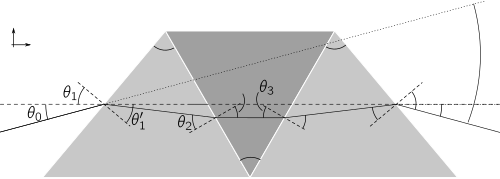
트리플트

더블아미치 프리즘은 보다 일반적인 트리플트 프리즘의 대칭 형태로서, 두 외부 원소의 정점각과 안경이 다를 수 있다(오른쪽 그림 참조).3중 프리즘은 광학 시스템에서는 거의 발견되지 않지만, 이중 아미치 설계를 넘어 3중 프리즘이 추가된 자유도는 분산 선형성을 개선할 수 있다.3중 프리즘의 편차 각도는 각 인터페이스에서 굴절 방정식을 연결함으로써 얻는다.^[6][7]

${\displaystyle{\begin{정렬}\theta _{1}&.=\theta _{0}+\alpha _{1}+{\tfrac{1}{2}}\alpha _{2}&,\theta '_{3}&, =\arcsin({\tfrac{{2}}{n_{3}}}\,\sin \theta_{3n_})\\\theta '_{1}&, =\arcsin({\tfrac{1}{n_{1}}}\,\sin \theta_{1})\quad&\theta _{4}&amp을 말한다.=\theta '_{3}-\alpha _{3}\\\theta _{2}&.=\theta '_{1}-\alpha _{1}&,\theta '_{4}&, =\arcsin(n_{3}\,\sin \theta _{4}.)\\\theta '_{2}&=\arcsin({\tfrac {n_{1}}{n_{2}}}\,\sin \theta _{2})&\theta _{5}&=\theta '_{4}+\alpha _{3}+{\tfrac {1}{2}}\alpha _{2}\\\theta _{3}&=\theta '_{2}-\alpha _{2}\end{aligned}}}$

여기에서 광선 편차 각도는 $\Delta {\displaystyle }$= ${\displaystyle {\theta \mathrm{}}_{}}$ 0 -${\displaystyle {}_{}{}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ ${\$ _${0$}-\$theta _{5}}$에 $의해$ 주어진다$.$

참고 항목

• 분산 프리즘

참조