코컬러링

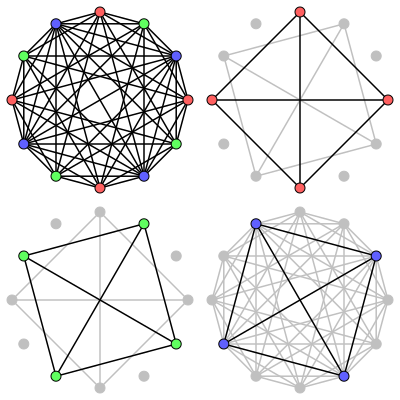
Cocoloring
3색(왼쪽 위 그림)을 사용한 코컬러: 이 그래프의 적절한 3색상은 불가능합니다.파란색 하위 그래프는 클리크(오른쪽 아래 그림)를 형성하고 빨간색 및 녹색 하위 그래프는 그래프 보완에서 클리크를 형성합니다.

그래프 이론에서 그래프 G의 공색(cocoloring)은 각 색 클래스가 G 또는 G의 보색에서 독립적인 집합을 형성하도록 정점에 색을 할당하는 것이다.G의 코크로매틱 수 z(G)는 G의 코크로매틱에 필요한 색 중 가장 적은 색이다.코크로매틱 번호 2의 그래프는 정확히 초당 그래프, 초당 그래프의 보완 그래프 및 분할 그래프입니다.

각 색상 클래스가 하나의 집단 또는 독립적이어야 한다는 요건이 착색 요건(각 색상 클래스가 독립된 세트여야 함)보다 약하고 서브컬러링(각 색상 클래스가 하나의 집단의 분리된 결합이어야 함)보다 강하기 때문에 G의 코크로매틱 수가 색 n보다 작거나 같아야 한다.G의 앰버이며, G의 아색수보다 크거나 같은 값이다.

Cocoloring은 Lesniak & Straight(1977년)에 의해 명명되고 처음 연구되었다.예르겐센(1995)은 임계 3-코크로매틱 그래프를 특징짓는 반면, 포민, 크라치 및 노벨리(2002)는 그래프의 코크로매틱 수를 근사하기 위한 알고리즘을 설명한다.Zverovich(2000)는 그래프 컬러링을 통한 완벽한 그래프의 정의와 유사한 완벽한 코크로매틱 그래프의 클래스를 정의하고 이러한 그래프의 금지된 하위 그래프 특성을 제공한다.

레퍼런스

  • 를 클릭합니다Fomin, Fedor V.; Kratsch, Dieter; Novelli, Jean-Christophe (2002), "Approximating minimum cocolourings", Inf. Process. Lett., 84 (5): 285–290, doi:10.1016/S0020-0190(02)00288-0.
  • 를 클릭합니다Gimbel, John; Straight, H. Joseph (1987), "Some topics in cochromatic theory", Graphs and Combinatorics, 3 (1): 255–265, doi:10.1007/BF01788548.
  • 를 클릭합니다Jørgensen, Leif K. (1995), "Critical 3-cochromatic graphs", Graphs and Combinatorics, 11 (3): 263–266, doi:10.1007/BF01793013.
  • 를 클릭합니다Lesniak, L.; Straight, H. J. (1977), "The cochromatic number of a graph", Ars Combinatoria, 3: 39–46.
  • 를 클릭합니다Straight, H. J. (1979), "Cochromatic number and the genus of a graph", Journal of Graph Theory, 3 (1): 43–51, doi:10.1002/jgt.3190030106.
  • 를 클릭합니다Zverovich, Igor V. (2000), Perfect cochromatic graphs, Research report RRR 16-2000, Rutgers University Center for Operations Research, archived from the original on 2016-03-03, retrieved 2006-10-16.