적응 공명 이론

Adaptive resonance theory

적응 공명 이론(ART)은 스티븐 그로스버그와 게일 카펜터에 의해 뇌가 정보를 처리하는 방법에 대한 측면에서 개발된 이론이다.지도 학습 방법과 비지도 학습 방법을 사용하는 다수의 신경 네트워크 모델을 설명하고 패턴 인식 및 예측과 같은 문제를 해결합니다.

ART 모델 뒤에 있는 주요 직관은 물체 식별과 인식이 일반적으로 '하향식' 관찰자 기대와 '하향식' 감각 정보의 상호작용의 결과로 일어난다는 것이다.이 모델은 '하향식' 기대치가 메모리 템플릿 또는 프로토타입의 형태를 취하며, 그 후 감각에 의해 감지된 물체의 실제 특징과 비교된다고 가정합니다.이 비교는 범주 소속성의 척도를 발생시킨다.감각과 기대 사이의 이 차이가 '휘도 매개 변수'라고 불리는 설정된 임계값을 초과하지 않는 한 감지된 물체는 예상 클래스의 멤버로 간주됩니다.따라서 시스템은 '가소성/안정성' 문제, 즉 증분 학습이라고도 하는 기존 지식을 방해하지 않고 새로운 지식을 습득하는 문제에 대한 해결책을 제공한다.

학습 모델

기본 ART 구조

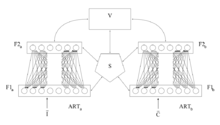
기본 ART 시스템은 감독되지 않은 학습 모델입니다.일반적으로 비교 필드 및 뉴런으로 구성된 인식 필드, 경계 매개 변수(인식의 임계값), 재설정 모듈로 구성된다.

  • 비교 필드는 입력 벡터(1차원 값 배열)를 가져와서 인식 필드에서 가장 일치하는 값으로 전송합니다.
    • 그것의 가장 좋은 매치는 무게 집합(무게 벡터)이 입력 벡터와 가장 가깝게 일치하는 단일 뉴런이다.
  • 각 인식장 뉴런은 음의 신호(입력 벡터에 대한 해당 뉴런의 일치 품질에 비례함)를 다른 인식장 뉴런 각각에 출력하여 출력을 억제한다.
    • 이러한 방법으로 인식 필드는 측면 억제를 나타내며, 그 안의 각 뉴런이 입력 벡터가 분류되는 카테고리를 나타낼 수 있도록 한다.
  • 입력 벡터가 분류된 후 리셋 모듈은 인식 일치의 강도를 경계 파라미터와 비교한다.
    • 경계 매개변수를 극복한 경우(즉, 입력 벡터가 이전 입력 벡터에서 볼 수 있는 정상 범위 내에 있음), 훈련이 시작됩니다.
      • 이긴 인식 뉴런의 무게는 입력 벡터의 특징에 맞게 조정된다.
    • 그렇지 않으면 일치 레벨이 경계 파라미터보다 낮으면(즉 입력 벡터의 일치가 그 뉴런에 대해 통상적인 예상 범위 밖에 있다) 당첨 인식 뉴런을 억제하고 탐색 절차를 실행한다.
      • 이 탐색 절차에서는 인식 일치에 의해 경계 파라미터가 극복될 때까지 리셋 기능에 의해 인식 뉴런을 하나씩 비활성화한다.
        • 특히, 탐색 절차의 각 사이클에서 가장 활성화된 인식 뉴런이 선택되고 활성화가 경계 매개 변수보다 낮으면 꺼진다.
        • (따라서 나머지 인식 뉴런이 억제에서 해방된다는 점에 유의하십시오).
    • 커밋된 인식 뉴런의 일치가 경계 파라미터를 넘지 않으면 커밋되지 않은 뉴런이 커밋되고 그 가중치는 입력 벡터에 일치하도록 조정된다.
  • 경계 매개 변수는 시스템에 상당한 영향을 미친다. 경계 수준이 높을수록 매우 상세한 기억(많은 세분화된 범주)이 생성되는 반면, 경계 수준이 낮을수록 더 일반적인 기억(적은 범주, 보다 일반적인 범주)이 발생한다.

트레이닝

ART 기반의 신경망을 훈련하는 데는 두 가지 기본적인 방법이 있다: 느린 것과 빠른 것이다.슬로우 러닝 방법에서는 입력 벡터에 대한 인식 뉴런 가중치의 훈련 정도가 미분방정식에 의한 연속값으로 계산되어 입력 벡터가 제시되는 시간의 길이에 의존하게 된다.빠른 학습에서는 가중치 조정 정도를 계산하기 위해 대수 방정식을 사용하고 이진수 값을 사용합니다.빠른 학습은 다양한 작업에 효과적이고 효율적이지만 느린 학습 방법은 생물학적으로 더 타당하며 연속 시간 네트워크(즉, 입력 벡터가 지속적으로 변할 수 있는 경우)와 함께 사용할 수 있다.

종류들

ART[1][2] 1은 이진수 입력만 받아들이는 가장 단순한 다양한 ART 네트워크입니다.ART[3] 2는 네트워크 기능을 확장하여 지속적인 입력을 지원합니다.ART 2-A는[4] ART-2의 간소화된 형태로 실행 시간이 대폭 단축되고 질적 결과가 ART-2의 완전한 구현보다 떨어지는 경우는 거의 없습니다.ART[5] 3은 시뮬레이션된 나트륨(Na+)과 칼슘(Ca2+) 이온 농도를 시스템 방정식에 통합함으로써 시냅스 활성의 기초적인 신경전달물질 조절을 시뮬레이션함으로써 ART-2를 기반으로 구축되며, 이는 불일치 재설정을 트리거하는 범주를 부분적으로 억제하는 생리적으로 더 현실적인 방법으로 귀결된다.

ARTMAP의 개요

ARTMAP[6]또한 예측 CAD로 알려진, 가장 먼저 단위이고, 두번째 단위는 올바른 출력 데이터에는 정확한 clas을 만들고 경계 변수에서 첫번째 단위의 최소 가능한 조정을 만드는데 사용되는 입력 데이터를 관리한 학습 구조로 두 약간 수정 ART-1 또는 ART-2 단위 결합한 것이다.sif아이시온

Fuzzy[7] ART는 ART의 패턴 인식에 퍼지 논리를 구현하여 일반화를 강화합니다.퍼지 ART의 선택적(그리고 매우 유용한) 기능은 패턴 분류에 기능의 부재를 통합하는 수단인 보완 코딩으로, 비효율적이고 불필요한 범주 확산을 방지하는 데 큰 도움이 된다.적용된 유사성 측정은 L1 표준에 기초한다.Fuzzy ART는 노이즈에 매우 민감한 것으로 알려져 있습니다.

퍼지[8] ARTMAP은 퍼지 ART 단위를 사용하는 아트맵일 뿐이므로 그에 상응하는 효과의 증가를 초래한다.

Simplified Fuzzy ARTMAP(SFAM)[9]는 분류 태스크 전용 퍼지 ARTMAP의 매우 단순화된 변형이다.

가우스[10] ART와 가우스[10] ARTMAP은 확률론에 기초한 가우스 활성화 함수와 연산을 사용한다.따라서 가우스 혼합 모델과 어느 정도 유사합니다.퍼지 ART와 퍼지 ARTMAP에 비해 소음에 덜 민감하다.그러나 학습된 표현의 안정성이 저하되어 개방형 학습 과제에서 범주의 확산을 초래할 수 있다.

Fusion ART 및 관련 네트워크는[11][12][13] ART와 ARTMAP을 여러 패턴 채널로 확장합니다.이들은 비지도 학습, 감독 학습 및 강화 학습을 포함한 몇 가지 학습 패러다임을 지원합니다.

TopoART는[14] 퍼지 ART와 증가하는 신경 가스와 같은 위상 학습 네트워크를 결합합니다.또, 노이즈 저감 메카니즘을 추가한다.TopoART를 추가 학습 패러다임으로 확장하는 몇 가지 파생 신경 네트워크가 있다.

하이퍼스피어[15] ART와 하이퍼스피어[15] ARTMAP은 각각 퍼지 ART와 퍼지 ARTMAP과 밀접한 관련이 있다.그러나 다른 유형의 범주 표현(즉, 하이퍼스피어)을 사용하기 때문에 [0, 1] 간격으로 입력을 정규화할 필요가 없습니다.그들은 L2 규범에 기초한 유사성 측정을 적용한다.

LAPART[16] Laterally Primed Adaptive Resonance Theory (LAPART) 신경 네트워크는 학습된 연관성을 기반으로 예측을 위한 메커니즘을 만들기 위해 두 개의 퍼지 ART 알고리즘을 결합합니다.2개의 Fuzzy ART의 결합은 시스템이 명확한 솔루션을 향해 빠르게 수렴할 수 있도록 하는 고유한 안정성을 가지고 있습니다.또한 퍼지 ARMAP과 유사한 논리적 추론 및 지도 학습을 수행할 수 있습니다.

비판

Fuzzy ART와 ART 1(즉, 학습된 범주)의 결과는 훈련 데이터가 처리되는 순서에 따라 결정적으로 좌우된다는 점에 주목했다.이 효과는 느린 학습 속도를 사용하여 어느 정도 줄일 수 있지만 입력 데이터 세트의 크기에 관계없이 존재합니다.따라서 Fuzzy ART와 ART 1 추정치는 [17]일관성의 통계적 특성을 가지고 있지 않다.이 문제는 양쪽 네트워크에서 안정적인 학습을 보장하는 각 메커니즘의 부작용으로 간주할 수 있습니다.

카테고리를 클러스터로 정리하는 TopoART나 Hyperphere TopoART 등의 보다 고도의 ART 네트워크는 클러스터 형상이 관련 카테고리의 작성 순서에 의존하지 않기 때문에 이 문제를 해결할 수 있다.(그림 3(g, h) 및 그림 4 참조).

레퍼런스

  1. ^ Carpenter, G.A. & Grossberg, S. (2003), 적응 공명 이론 2006-05-19년 마이클 A. 웨이백 머신에서 아카이브. Arbib(Ed.), 뇌 이론 및 신경 네트워크 핸드북, 제2판(87-90페이지)케임브리지, 매사추세츠: MIT 프레스
  2. ^ Grossberg, S.(1987), 경쟁력 학습: 인터랙티브 활성화에서 적응 공명으로 2006-09-07 Wayback Machine, 인지과학(저널), 11, 23-63에 아카이브됨
  3. ^ Carpenter, G.A. & Grossberg, S.(1987), ART 2: 아날로그 입력 패턴에 대한 안정적인 카테고리 인식 코드 자체 구성 2006-09-04 아카이브, Applied Optics, 26(23), 4919-4930
  4. ^ Carpenter, G.A., Grossberg, S. 및 Rosen, D.B.(1991a), ART 2-A: 신속한 카테고리 학습 및 인식을 위한 적응형 공진 알고리즘 2006-05-19 Wayback Machine, Neural Networks, 4, 493-504에 보관됨
  5. ^ Carpenter, G.A. & Grossberg, S.(1990), ART 3: 자기조직화 패턴인식 아키텍처에서 화학적 송신기를 사용한 계층적 검색 2006-09-06년 Neural Networks 웨이백 머신, 3, 129-152 아카이브
  6. ^ 카펜터, G.A., Grossberg, S. 및 레이놀즈, J.H.(1991) ARTMAP: 자기조직화 신경망에 의한 비정상 데이터의 실시간 학습 및 분류 2006-05-19 Wayback Machine, Neural Networks, 4,565-588,
  7. ^ Carpenter, G.A., Grossberg, S., Rosen, D.B.(1991b), Fuzzy ART: 적응 공명 시스템에 의한 아날로그 패턴의 빠르고 안정적인 학습 및 분류 2006-05-19 Wayback Machine, Neural Networks, 4, 759-771에 보관됨
  8. ^ Carpenter, G.A., Grossberg, S., Markuzon, N., 레이놀즈, J.H. 및 Rosen, D.B.(1992) Fuzy ARMAP: 아날로그 다차원 맵의 증분 지도 학습을 위한 뉴럴 네트워크 아키텍처 IEEE 웨이백 머신에서 2006-05-19에 보관된 뉴럴 네트워크 아키텍처
  9. ^ 모하마드-타기-바킬-바흐미셰와 니콜라 파베시치.(2003) Fast Simplified Fuzzy ARMAP 네트워크, Neural Processing Letters, 17(3):273~316
  10. ^ a b 제임스 R.Williamson.(1996), 가우스 아트맵: 노이즈가 많은 다차원 지도의 빠른 증분 학습을 위한 뉴럴 네트워크, 뉴럴 네트워크, 9(5):881-897
  11. ^ Y.R. Asfour, G.A. Carpenter, S. Grossberg 및 G.W. Lesher.(1993) Fusion ARMAP: 다중 채널 분류를 위한 적응형 퍼지 네트워크.인: 제3회 산업 퍼지 제어 및 인텔리전트 시스템에 관한 국제 회의(IFIS)의 진행.
  12. ^ Tan, A.-H.; Carpenter, G. A.; Grossberg, S. (2007). Liu, D.; Fei, S.; Hou, Z.-G.; Zhang, H.; Sun, C. (eds.). "Intelligence Through Interaction: Towards a Unified Theory for Learning". Advances in Neural Networks – ISNN 2007. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer: 1094–1103. doi:10.1007/978-3-540-72383-7_128. ISBN 978-3-540-72383-7.
  13. ^ Tan, A.-H.; Subagdja, B.; Wang, D.; Meng, L. (2019). "Self-organizing neural networks for universal learning and multimodal memory encoding". Neural Networks. 120: 58–73. doi:10.1016/j.neunet.2019.08.020.
  14. ^ 마르코 체어파노우.(2010) TopoART: 위상학습 계층형 ART 네트워크, In: 인공신경망에 관한 국제회의의 진행, Part III, LNCS 6354, 157-167
  15. ^ a b 게오르기오스 C.아나그노스토풀로스와 마이클 게오르기오풀로스.(2000), 비지도 및 지도 증분 학습을 위한 하이퍼스피어 ART 및 ARMAP, In: 신경망에 관한 국제 공동 회의의 진행, vol.6, 59-64
  16. ^ Sandia National Laboratories (2017) Lapart-Python 문서
  17. ^ Sarle, Warren S.(1995), 통계학자가 Wayback Machine에 보관된 2011년 7월 20일
  18. ^ 마르코 체어파노우.(2012) 초구형 카테고리를 이용한 토폴로지 학습 계층형 ART 뉴럴 네트워크를 이용한 증분 온라인 클러스터링, In: 데이터 마이닝 산업회의 포스터 및 업계 진행, 22-34

Wasserman, Philip D.(1989), 뉴럴 컴퓨팅: 이론과 실천, 뉴욕: Van Nostrand Reinhold, ISBN 0-442-20743-3

외부 링크