비너-아라야 그래프
Wiener–Araya graph| 비에너아라야 그래프 | |
|---|---|
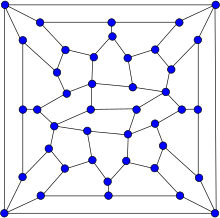 | |
| 정점 | 42 |
| 가장자리 | 67 |
| 반지름 | 5 |
| 지름 | 7 |
| 둘레 | 4 |
| 자동형성 | 2 |
| 색수 | 3 |
| 색도 지수 | 4 |
| 특성. | 차하밀턴주의 플라나르 |
| 그래프 및 모수 표 | |
위너-아라야 그래프는 그래프 이론에서 67개의 가장자리가 있는 42개의 꼭지점에 대한 그래프다.그것은 저자극인데, 이것은 그것 자체가 해밀턴 사이클을 가지고 있지 않지만 그것으로부터 하나의 꼭지점을 제거함으로써 형성된 모든 그래프는 해밀턴 사이클을 가지고 있다는 것을 의미한다.그것은 또한 평면적이다.
역사
저자극 그래프들은 처음에 Souseler에 의해 Problémes 격자무늬와 골자체에 의해 연구되었다.[1]1967년에 린드그렌은 하아해밀턴식 그래프의 무한 시퀀스를 구축했다.[2]그는 처음에 이 주제에 대한 선구자로 가우딘, 헤르츠, 로시,[3] 그 다음 부세커, 사티를[4] 꼽았다.
처음부터 가장 작은 피하밀턴 그래프가 알려져 있다: 피터슨 그래프.그러나, 가장 작은 평면형 피하밀턴 그래프에 대한 사냥은 계속된다.이 문제는 1973년 바클라프 차바탈에 의해 처음 제기되었다.[5]첫 번째 후보 답안은 1976년 카스텐 토마센이 105-토마센 그래프에서 제시하였다.[6]1979년, Hatzel은 57 정점에 있는 평면 저자극 그래프: Hatzel 그래프로 이 결과를 개선했다.[7]이 바운드는 2007년 48-Zamfirescu 그래프에 의해 낮아졌다.[8]
2009년 가보르 비에너와 마코토 아라야가 만든 그래프는 알려진 것 중 가장 작은 평면형 피하밀턴식 그래프가 되었다(정점 42로).[9][10]그들의 논문에서, 비너와 아라야는 그들의 그래프의 질서가 더글라스 아담스의 소설인 "Hitchhiker's Guide to the Galaxy"의 답으로 보인다고 주장하면서 그들의 그래프의 질서가 최적의 것이라고 추측했다.
참조
- ^ Sousselier, R. (1963), Problème no. 29: Le cercle des irascibles, vol. 7, Rev. Franç. Rech. Opérationnelle, pp. 405–406
- ^ Lindgren, W. F. (1967), "An infinite class of hypohamiltonian graphs", American Mathematical Monthly, 74: 1087–1089, doi:10.2307/2313617, MR 0224501
- ^ Gaudin, T.; Herz, P.; Rossi (1964), "Solution du problème No. 29", Rev. Franç. Rech. Opérationnelle (in French), 8: 214–218
- ^ Busacker, R. G.; Saaty, T. L. (1965), Finite Graphs and Networks
- ^ Chvátal, V. (1973), "Flip-flops in hypo-Hamiltonian graphs", Canadian Mathematical Bulletin, 16: 33–41, doi:10.4153/cmb-1973-008-9, MR 0371722
- ^ Thomassen, Carsten (1976), "Planar and infinite hypohamiltonian and hypotraceable graphs", Discrete Mathematics, 14 (4): 377–389, doi:10.1016/0012-365x(76)90071-6, MR 0422086
- ^ Hatzel, Wolfgang (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Mathematische Annalen (in German), 243 (3): 213–216, doi:10.1007/BF01424541, MR 0548801
- ^ Zamfirescu, Carol T.; Zamfirescu, Tudor I. (2007), "A planar hypohamiltonian graph with 48 vertices", Journal of Graph Theory, 55 (4): 338–342, doi:10.1002/jgt.20241, MR 2336805
- ^ Wiener, Gábor; Araya, Makoto (April 20, 2009), The ultimate question, arXiv:0904.3012, Bibcode:2009arXiv0904.3012W.
- ^ Wiener, Gábor; Araya, Makoto (2011), "On planar hypohamiltonian graphs", Journal of Graph Theory, 67 (1): 55–68, doi:10.1002/jgt.20513, MR 2809563.


