테일러 칼럼

테일러 칼럼은 코리올리 효과의 결과로 발생하는 유체역학 현상이다. 그것은 제프리 잉그램 테일러의 이름을 따서 지어졌다. 단단한 몸체에 의해 동요되는 회전 유체는 테일러 기둥이라고 불리는 회전축과 평행한 기둥을 형성하는 경향이 있다.

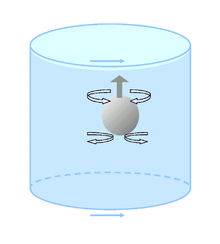
회전하는 유체의 회전축에 평행하게 움직이는 물체는 회전하지 않는 유체에서 경험하는 것보다 더 많은 드래그력을 경험한다. 예를 들어 강하게 부력하는 공(탁구공 등)은 회전하지 않는 유체에서보다 더 느리게 표면으로 떠오를 것이다. 코리올리 효과로 인해 바깥쪽으로 밀려나오는 공의 경로에 있는 액체가 다시 옮겨갈 정도로 순환하는 경향이 있기 때문이다. 회전 속도가 빠를수록 유체에 의해 움직이는 관성 원의 반지름이 작아진다.

회전하지 않는 유체에서는 상승 볼 위의 유체 부분과 그 아래에 닫히면서 공에 대한 저항력이 상대적으로 거의 없다. 회전하는 유체에서 볼은 그 위에 있는 유체의 전체 기둥을 위로 밀어 올려야 하고, 표면으로 떠오르려면 유체의 전체 기둥을 그 아래를 따라 끌어야 한다.

따라서 회전하는 유체는 어느 정도의 강성을 나타낸다.

역사

테일러 칼럼은 윌리엄 톰슨, 켈빈 경에 의해 1868년에 처음 관찰되었다.^[1][2] 테일러 칼럼은 1881년^[3] 켈빈과 1890년 존 페리의 강연 시연에 실렸다.^[4] 이 현상은 테일러-프라우드만 정리를 통해 설명되며, 테일러,^[5] 그레이스,^[6] 스튜어트슨,^[7] 맥스워시^[8] 등이 조사하였다.

이론

테일러 칼럼은 엄격하게 연구되어 왔다. Rel<1, Ek<1, Ro<1>, 반지름 실린더의 드래그 방정식, a, 다음과 같은 관계가 발견되었다.^[7][9]

${\displaystyle F={\frac {16}{3}}\rho a^{3}\오메가 U}$

이를 도출하기 위해 무어와 사프만은 선형화된 나비에를 해결했다.–^[9]점성 항의 수직 및 방사형 구성 요소 중 일부가 코리올리스 용어에 비해 작은 것으로 간주되는 원통형 좌표에서의 스톡스 방정식:

${\displaystyle -2\Oomega v=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}}}}$

${\displaystyle 2\Oomega u=\nu \left({\frac {\partial ^{2}v}{\partial r^{1}:{1}}}+{\prac {1}{partial v}{\partial r}{v^{2}}:}\오른쪽)}$

${\displaystyle 0=-{\frac {1}{\rho}}{\frac {\frac {\frac}{\frac}{{2}w}{\propert r^{1}}}{\frac {1}{\frac {\1}{\frac {}}}}}{\frac {\fraz{{}}}}}}\reason w}\reason r}\rh}\right)}}}}}}}}}}}}}}}}}}}}}}}$

이러한 방정식을 해결하기 위해 볼륨 보존 조건도 통합한다.

${\displaystyle {\frac {1}{r}{\frac {\frac(ur)}{\preason r}{\frac {\preason w}{\preason z}=0}}$

우리는 디스크 표면에서 속도 형태를 제한하기 위해 Ekman 호환성 관계를 사용한다.

${\displaystyle w-U=\pm {\frac {1}{2}}: {\sqrt {\nu }{\no }}{\frac {1}{r}{\frac {\partial (rv)}{\partial r}}}}}}$

결과 속도 장은 베셀 함수의 측면에서 해결할 수 있다.

${\displaystyle u=-{\frac {\nu }{2\Oomega }}\int \limits _{0}^{0}{0^{{0}}}}A(k)J_{1}{1}(kr)e^{-\nu k^{3}z/2\Oomega}dk}$

${\displaystyle v=\int \limits _{0}^{\\infit }A(k)J_{1}{1}(kr)e^{-\nu k^{3}z/2\Oomega }dk}$

${\displaystyle w=-\int \limits _{0}^{\ft }A(k)J_{0}(kr)e^{-\nu k^{3}z/2\오메가 }dk}$

Ek<1>에 의해 A(k)라는 기능이 주어지는 경우,

${\displaystyle A(k)={\frac {2Ua}{\pi}}\왼쪽(\cosa ka-{\frac {\sin ka}{ka}}\오른쪽)}$

v에 대한 방정식을 통합하면 압력과 따라서 첫 번째 방정식에 의해 주어지는 드래그력을 찾을 수 있다.

참조

추가 읽기

• Brenner, Michael P.; Stone, Howard A. (May 2000). "Modern Classical Physics Through the Work of G. I. Taylor". Physics Today. 53 (5): 30–35. Bibcode:2000PhT....53e..30B. doi:10.1063/1.883100.

외부 링크

• 테일러 칼럼(마르타 버클리, MIT)
• 기록 플레이어 유체 역학: 테일러 칼럼 실험(UCLA 스핀 랩)