경사 편향법

경사편향법은 1914년 조지 A가 도입한 보 및 프레임의 구조해석법이다.경사 ^[1]편향법은 모멘트 분포법이 개발되기 전까지 10년 이상 널리 사용되었다.J가 쓴 "현대 골조 구조의 이론과 실천"이라는 책.B 존슨, C.W. 브라이언, F.E.Turneaure, 이 방법은 "독일의 오토 모어 교수에 의해 처음 개발되었고 나중에 G.A. Maney 교수에 의해 독립적으로 개발되었습니다."이 책에 따르면 오토 모어 교수는 그의 저서 '강체결절을 가진 트러스의 평가' 또는 '스타렌 노텐베르동겐'에서 이 방법을 처음으로 도입했다.

서론

경사편향식을 형성하여 접합 및 전단균형조건을 적용함으로써 회전각(또는 경사각)을 산출한다.이들을 다시 경사편향방정식으로 치환함으로써 부재단 모멘트를 쉽게 구할 수 있다.부재의 변형은 휨 모멘트에 의한 것입니다.

경사 편향 방정식

기울기 편향 방정식은 강성 $계수{\displaystyle }$ ${\displaystyle K\frac{{}_{}}{}}$ ${\displaystyle =}$ ${\displaystyle \frac{I_{}}{}}$ a ${\displaystyle \frac{b_{}}{}}$ L ${\displaystyle \frac{a_{}}{}}$b {{$displaystyle$ K=$ac {I_{ab}}}$ {$L_{ab}}}$ 및$$ 코드 $회전{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{L_{}}{}}$ a ${\displaystyle \frac{b_{}}{}}${$displaystyle \psi$=$brac {Delta$} {$L_{ab$를 사용하여 작성할 수도 있습니다.

경사 편향 방정식의 도출

$길이{\displaystyle {}_{}}$ L ${\displaystyle a_{}}$ b$(\$ab}) 및$$ 굽힘 $강성{\displaystyle {}_{}}$ ${\displaystyle E_{}}$ a ${\displaystyle {}_{}{}_{}}$ ${\displaystyle I_{}}$ ${\displaystyle a_{}}$ b$(\$의 단순한 빔이 있는 경우$I_{ab}$은(는) 시계방향 $모멘트{\displaystyle {}_{}}$ M ${\displaystyle a_{}}$ ${\displaystyle b_{}}$({$displaystyle$M_{$ab})$와 M ${\displaystyle b_{}}$ ${\displaystyle a_{}}${$displaystyle M_{ba$로 양끝에 로드되며 멤버 엔드는 같은 방향으로 회전합니다.이러한 회전각은 단위력법 또는 다아시의 법칙을 사용하여 계산할 수 있습니다.

$\displaystyle \theta _{a}-{\frac {Delta}{L_{ab}}=blac {L_{ab}}{3}E_{ab}I_{ab}}M_{ab}-{\frac {L_{ab}}{6}E_{ab}I_{ab}}M_{ba}}$

$\displaystyle \theta _{b}-{\frac {Delta }{L_{ab}}=-{\frac {L_{ab}}{6}E_{ab}I_{ab}}M_{ab}+{\frac {L_{ab}}{3}E_{ab}I_{ab}}M_{ba}}$

이러한 방정식을 재배치하여 경사 편향 방정식을 도출합니다.

평형 상태

관절균형

관절 평형 조건은 자유도를 가진 각 관절이 평형 상태에 있는 불균형 모멘트를 갖지 않아야 한다는 것을 의미한다.그러므로,

$\displaystyle \Sigma \left(M^{f}+M_{member}\right)=\Sigma M_{joint}$

여기서 M ${\displaystyle m_{}}$ ${\displaystyle m_{}}$ ${\displaystyle b_{}}$ ${\displaystyle r_{}}${ $display$ style M _ { $member$} 、 M ${\displaystyle f^{}}${ $display$ $style$ M^ { $f$} 、 ${\displaystyle M_{}}$ ${\displaystyle j_{}}$ ${\displaystyle o_{}}$ n ${\displaystyle t_{}}${ $joint$} $the{\displaystyle {}_{}}$$$ the joint joint the joint the joint joint at$$ joint joint joint joint joint joint joint joint joint joint joint joint joint joint joint here here here moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments$$ moments moments moments moments moments moments moments moments moments moments moments moments moments moments moments

전단 평형

프레임에 현 회전이 있을 경우 추가 평형 조건, 즉 전단 평형 조건을 고려해야 한다.

예

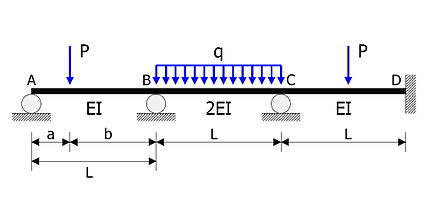
그림에 표시된 정적 불확정 빔을 분석해야 합니다.

• 멤버 AB, BC, CD의 $길이$는 L ${\displaystyle =}$ ${\displaystyle \text{10}}$ m$$（ \ $displaystyle$ L =$10$\$m$ 。
• 굽힘 강성은 각각 EI, 2EI, EI입니다.
• $규모{\displaystyle }$ P ${\displaystyle =}$ ${\displaystyle \text{10}}$ $(\displaystyle$ P$=10\kN)$의 집중 하중은 지지대 A에서 a ${\displaystyle =}$ ${\displaystyle \text{3}}$m(\$displaystyle$ a$=3\m)$ $거리$에 작용한다.
• $강도{\displaystyle }$ ${\displaystyle \mathrm{q}}$ ${\displaystyle =}$ ${\displaystyle \mathrm{1k}}$ N${\displaystyle /m}${$displaystyle$ q$=1\kN/m}$의 균일 부하가 BC에 작용합니다.
• $Member{\displaystyle }$ CD는 진도 ${\displaystyle \mathrm{P}}$ ${\displaystyle =}$ ${\displaystyle \text{10}}$ ${\displaystyle k}$ N$({displaystyle$ P$=10\kN$의 집중 부하로 중간 스팬에 로드됩니다.

다음 계산에서는 시계 방향의 모멘트와 회전이 양수입니다.

자유도

조인트 A, B, C의 회전각도 ${\displaystyle {\theta }_{}}$ A$,$ $B$$, B,$ C의 회전각도$$ $B$ B$, C$ $C$의 회전각도는 $미지수$로 $한다$.서포트 침하를 포함한 다른 원인에 의한 코드 회전은 없습니다.

고정 종료 모멘트

고정 종료 모멘트는 다음과 같습니다.

${\displaystyle M_{AB}^{f}=-{\frac {Pab^{2}}{L^{2}}=-{\frac {10\times 7^{2}}=-14.7\mathrm {,kN,m}}}$

${\displaystyle M_{BA}^{f}=pa frac {Pa^{2}b}{L^{2}}=bsfrac {10\times 3^{2}\times 7}{10^{2}}=6.3\mathrm {,kN,m} }$

${\displaystyle M_{BC}^{f}=-{\frac {qL^{2}}{12}=-{\frac {1\times 10^{2}}{12}=-8.333\mathrm {,kN,m}}}}}$

${\displaystyle M_{CB}^{f}=black {qL^{2}}{12}=black {1\times 10^{2}}{12}=8.333\mathrm {,kN,m}}}}$

${\displaystyle M_{CD}^{f}=-{\frac {PL}{8}=-{\frac {10\times 10}{8}=-12.5\mathrm {,kN,m}}}}$

${\displaystyle M_{DC}^{f}=black {PL}{8}=black {10\times 10}{8}=12.5\mathrm {,kN,m}}}$

경사 편향 방정식

기울기 편향 방정식은 다음과 같이 구성됩니다.

${\displaystyle M_{AB}=paramfrac {EI}{L}}\left(4\theta_{A}+2\theta_{B}\right)=paramfrac {4EI\theta _{A}+2EI\theta _{B}}{L}}$

${\displaystyle M_{BA}=paramfrac {EI}{L}}\left(2\theta_{A}+4\theta_{B}\right)=paramfrac {2EI\theta _{A}+4EI\theta _{B}}{L}}$

${\displaystyle M_{BC}=420 frac {2EI}{L}}\left(4\theta_{B}+2\theta_{C}\right)=secfrac{8EI\theta _{B}+4EI\theta _{C}}{L}}$

${\displaystyle M_{CB}=420 frac {2EI}{L}}\left(2\theta_{B}+4\theta_{C}\right)=secfrac{4}EI\theta _{B}+8EI\theta _{C}}{L}}$

${\displaystyle M_{CD}=black {EI}{L}}\left(4\theta_{C}\right)=black {4}EI\theta _{C}}{L}}$

${\displaystyle M_{DC}=paramfrac {EI}{L}}\left(2\theta_{C}\right)=paramfrac {2EI\theta _{C}}{L}}$

결합 평형 방정식

관절 A, B, C는 평형 조건으로 충분해야 한다.그러므로

$\displaystyle \Sigma M_{A}=M_{AB}+M_{AB}^{f}=0.4EI\theta _{A}+0.2EI\theta _{B}-14.7=0}$

$\displaystyle \Sigma M_{B}=M_{BA}+M_{B}A}^{f}+M_{BC}+M_{BC}^{f}=0.2EI\theta _{A}+1.2EI\theta _{B}+0.4EI\theta _{C}-2.033=0}$

$\displaystyle \Sigma M_{CB}+M_{CB}^{f}+M_{CD}+M_{f}=0.4EI\theta _{B}+1.2EI\theta _{C}-4.167=0}$

회전각

회전 각도는 위의 연립 방정식에서 계산됩니다.

${\displaystyle \theta _{A}=420frac {40.219}I}}}$

${\displaystyle \theta _{B}=420frac {-6.937}{EI}}}$

${\displaystyle \theta _{C}=black {5.785}{EI}}}$

멤버 종료 모멘트

이러한 값을 다시 기울기 편향 방정식으로 치환하면 멤버의 끝 모멘트(kNm 단위)가 생성됩니다.

${\displaystyle M_{AB}=0.4배 40.219+0.2 \ times \ leftparam6.937\right)-14.7=0}$

${\displaystyle M_{BA}=0.2\times 40.219+0.4 \ times \ left pright 6 . 937 \ right ) + 6 . 3 = 11 . 57 }$

$\displaystyle M_{BC}=0.8배 \left6.937\right)+0.4\times 5.785-8.333=-11.57}$

$\displaystyle M_{CB}=0.4배 \left6.937\right)+0.8 \ times 5 . 785 + 8 . 333 = 10 . 19 }$

${\displaystyle M_{CD}=0.4\times -5.785-12.5=-10.19}$

${\displaystyle M_{DC}=0.2\times -5.785+12.5=13.66}$

「 」를 참조해 주세요.

• 비임 이론

메모들

레퍼런스

• Norris, Charles Head; John Benson Wilbur; Senol Utku (1976). Elementary Structural Analysis (3rd ed.). McGraw-Hill. pp. 313–326. ISBN 0-07-047256-4.
• McCormac, Jack C.; Nelson, James K. Jr. (1997). Structural Analysis: A Classical and Matrix Approach (2nd ed.). Addison-Wesley. pp. 430–451. ISBN 0-673-99753-7.
• Yang, Chang-hyeon (2001-01-10). Structural Analysis (in Korean) (4th ed.). Seoul: Cheong Moon Gak Publishers. pp. 357–389. ISBN 89-7088-709-1. Archived from the original on 2007-10-08.