슬레피안-울프 부호화

정보이론
엔트로피 미분 엔트로피 조건부 엔트로피 관절 엔트로피 상호정보 조건상호정보 상대 엔트로피 엔트로피 레이트 이산형 점의 밀도 제한
점증적 설비 특성 비율-분산 이론
섀넌의 소스 코딩 정리 채널 용량 노이즈 채널 코딩 정리 섀넌-하틀리 정리
v t

정보이론과 통신에 있어서 슬레피안-슬레피안-로 알려진 울프 부호화Wolf bound는 David Slepian과 Jack Wolf에 의해 1973년에 발견된 분산된 소스 코딩의 결과물이다. 이론적으로 두 개의 무손실 압축 상관 선원을 코딩하는 방법이다.^[1]

문제 설정

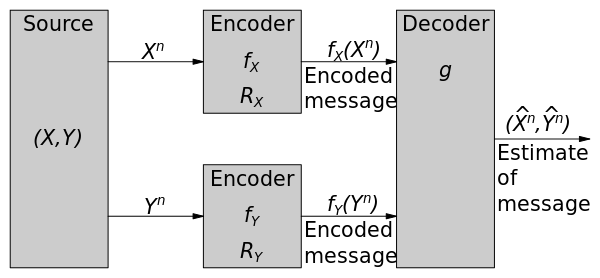
분산 코딩은 이 경우 별도의 인코더와 공동 디코더를 사용하여 2개 또는 더 종속적인 선원을 코딩하는 것이다. 통계적으로 의존하는 두 개의 유한 알파벳 랜덤 시퀀스 ${\displaystyle {Xn}^{}}$ ${\$ 및 ${\displaystyle {Yn}^{}}$ ${\$ Y$^{n},$Slepian–Wolf 정리는 두 선원의 분산 코딩에 대한 무손실 코딩 비율에 대한 이론적 결합을 제공한다.

정리

무손실 코딩 비율에 대한 경계는 다음과 같다.^[1]

${\displaystyle R_{X}\geq H(X Y),\,}$

${\displaystyle R_{Y}\geq H(Y X),\,}$

${\displaystyle R_{X}+R_{{Y}\geq H(X,Y).\,}$

If both the encoder and the decoder of the two sources are independent, the lowest rate it can achieve for lossless compression is ${\displaystyle H(X)}$ and ${\displaystyle H(Y)}$ for ${\displaystyle X}$ and ${\displaystyle Y}$ respectively, where ${\displaystyle H(X)}$ and ${\$디스플레이 $스타일 H(Y)}$은(는$)$ X {\$displaystyle$ $X$}과(와) Y {\$displaystyle$ Y$\}$의 엔트로피지만, 공동 디코딩을 통해 긴 시퀀스에 대한 소멸 오류 확률을 허용하면 슬레피안–늑대 정리는 훨씬 더 나은 압축률을 달성할 수 있다는 것을 보여준다. $X{\displaystyle }$ ${\displaystyle X}$ 및 $Y$ ${\displaystyle Y}$의 총 비율이 공동$$ 엔트로피 $H{\displaystyle (X,}$ ${\displaystyle Y)}$ ${\displaystyle H(X,Y)}$보다 크고 어떤$$ 소스도 엔트로피보다 작은 비율로 인코딩되지 않는 한 분산 코딩은 긴 시퀀스에 대해 임의로 작은 오류 확률을 달성할 수 있다.^[1]

분산 코딩의 특별한 경우는 디코더 측 정보가 포함된 압축으로, 여기서 소스 $Y{\displaystyle }$ ${\displaystyle Y}$은(는) 디코더 측에서는 사용할 수 있지만$$ 인코더 측에서는 액세스할 수 없다. This can be treated as the condition that ${\displaystyle R_{Y}=H(Y)}$ has already been used to encode ${\displaystyle Y}$, while we intend to use ${\displaystyle H(X Y)}$ to encode ${\displaystyle X}$. In other words, two isolated sources can compress data as efficiently as if they were 서로 의사소통하는 것. 전체 시스템이 비대칭적으로 작동하고 있다(두 선원에 대한 압축률은 비대칭이다).^[1]

이 경계는 토마스 M에 의해 두 개 이상의 상관관계가 있는 출처의 사례로 확대되었다. 1975년에 커버를 했고,^[2] 1976년에 아론 D에 의해 비슷한 결과를 얻었다. 와이너와 제이콥 지브는 가우스 공동 출처의 손실 코딩에 관하여.^[3]

참고 항목

• 데이터 압축
• 데이터 동기화
  • 동기화(컴퓨터 과학)
• 디커스
• 정보 이론 연대표

참조

원천

외부 링크