세트(카드 게임)

세트
유형	실시간
플레이어스	1+
필요한 기술	시각화, 논리적 추론, 집중력
카드	81

세트 데크에서 카드 3장.이 카드들은 각각 고유한 번호, 기호, 음영, 색상을 가지고 있으며, 따라서 "세트"가 된다.

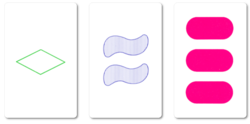
세트(SET로 표기)는 1974년 마샤 팔코가 디자인하고 1991년 세트 엔터프라이즈가 발행한 실시간 카드 게임이다.데크는 모양 수(1개, 2개 또는 3개), 모양(다이아몬드, 스퀴글, 타원형), 음영(솔리드, 스트라이프 또는 오픈), 색상(빨간색, 녹색 또는 보라색) 등 세 가지 특징에 걸쳐 네 가지 특징이 다른 81개의 고유 카드로 구성된다.^[1]각각의 가능한 특징들의 조합 (예: 세 개의 줄무늬 녹색 다이아몬드가 있는 카드)은 정확히 한 번 데크에 카드로서 나타난다.

이 게임에서, 3개의 카드의 특정한 조합은 한 세트를 구성하고 있다고 한다.색상, 숫자, 모양 및 음영 등 네 가지 특징 범주 각각에 대해 세 가지 카드는 모두 다른 a) 또는 b)로 해당 특징을 표시해야 한다.다른 방법을 사용하십시오. 각 기능에 대해 세 개의 카드는 한 버전의 기능을 보여주는 두 개의 카드와 다른 버전을 표시하는 나머지 카드를 사용하지 마십시오.

예를 들어, 3장의 카드 조각은 모두 같은 반면, 숫자, 색상, 모양은 모두 다르기 때문에 3장의 솔리드 레드 다이아몬드와 2개의 솔리드 그린 스퀴글, 1개의 솔리드 보라색 타원형이 한 세트를 형성한다.

어떤 "set"에 대해서도, 모두 동일한 형상의 수와 다른 형상의 수는 0과 같은 + 4의 차이, 또는 1과 같은 + 3의 차이, 또는 2와 같은 + 2의 차이, 또는 3과 같은 + 1의 차이로 분해할 수 없다.(카드의 경우와 동일한 + 0의 차이, 4의 형상의 차이, 그리고 카드와 동일한 + 0의 차이로서 분해할 수 없으며, 존재하지 않는다.세트 데크의 동일한 카드)

역사

이 게임은 디자이너가 유전학자라는 직업에서 사용했던 코딩 시스템에서 발전했다.^[2]세트는 1991년 아메리칸 멘사의 멘사 셀렉트 상을 수상했으며 1995년 디우츠셔 스필 프레이스에서 9위에 올랐다.

게임.

플레이 세트

이 카드들로 여러 게임을 할 수 있는데, 모두 세트라는 개념을 포함한다.세트는 다음 조건을 모두 만족하는 세 개의 카드로 구성된다.

그들은 모두 같은 번호를 가지고 있거나 세 개의 다른 번호를 가지고 있다.
그들은 모두 같은 모양을 가지고 있거나 세 개의 다른 모양을 가지고 있다.
그들은 모두 같은 음영을 가지고 있거나 세 개의 다른 음영을 가지고 있다.
그들은 모두 같은 색을 가지고 있거나 세 가지 다른 색을 가지고 있다.

세트의 규칙은 다음과 같이 요약된다: 세 개의 카드 그룹을 "2개의 ___와 1개의 ___"로 분류할 수 있다면, 그것은 집합이 아니다.

예를 들어 다음과 같은 세 가지 카드가 한 세트를 형성한다.

빨간 줄무늬 다이아몬드 하나
붉은 고형 다이아몬드 두 개
세 개의 빨간 오픈 다이아몬드

갑판으로부터 어떤 두 장의 카드라도 주어지면, 그것들과 한 세트를 이루는 다른 한 장의 카드가 있다.

표준 세트 게임에서 딜러는 12명이 눕거나 누군가 세트를 보고 "세트!"라고 부를 때까지 테이블에 카드를 놓는다.'셋트'라고 부른 선수가 세트의 카드를 가져가고, 딜러는 12명이 테이블에 오를 때까지 카드를 계속 나눠준다.12장의 카드 중 세트를 본 플레이어가 '세트'를 불러 세 장의 카드를 가져가고, 딜러는 세 장의 카드를 탁자 위에 더 놓는다.("설정"을 외치고 빨리 하나를 선택하지 않으면 패널티가 발생한다.)12장의 카드 중 세트가 없을 수도 있다. 이 경우 딜러는 15장의 카드를 만들기 위해 3장의 카드를 더, 즉 필요에 따라 18장 이상을 더 거래한다.3인 3조로 처리하고 세트를 찾는 이러한 과정은 갑판이 소진되고 테이블 위에 더 이상 세트가 없을 때까지 계속된다.이 시점에서 가장 많은 세트를 모은 사람이 승리한다.

세트 게임에는 다양한 변형들이 포함되었는데, 세트들을 찾기 위한 다른 기계학들과 다른 플레이어들의 상호 작용도 포함된다.그 게임의 열렬한 플레이어에 의해 추가적인 변종이 계속해서 만들어지고 있다.^[3]^[4]

세트의 기본 콤비네이터

전체 81개의 카드 세트와 게임 세트의 카드들이 4가지 특징들의 가능한 모든 조합을 보여준다.각 3×3 그룹을 4차원 공간에 정렬된 평면으로 간주하여, 한 세트는 한 줄(4차원)에 3장의 카드로 구성되며, 둘레가 있다.예를 들어 20-카드 캡 세트는 노란색으로 음영 처리된다.

어떤 두 개의 카드를 주더라도, 그 두 개의 카드로 세트를 구성하는 카드가 정확히 한 개 있다.따라서 전체 데크에서 무작위로 그려진 3장의 카드로부터 세트를 제작할 확률은 1/79이다.
캡 집합은 어떤 집합도 취할 수 없는 집합 레이아웃을 설명하는 수학적 구조물이다.세트를 만들지 않고도 합칠 수 있는 가장 큰 카드군은 20개다.^[5]^[6]이러한 그룹을 최대 캡 세트(OEIS에서는 시퀀스 A090245)라고 한다.도널드 크누스는 2001년에 81 카드 버전의 세트용 20사이즈의 캡 세트가 682344개 있다는 것을 발견했다; 4차원 유한 공간에 대한 부착형 변환에서는 모두 기본적으로 하나의 캡 세트로 축소된다.
$\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ ) $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ = $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ = $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ ${\$ {81 $\time$ 80 $}{2\time$ 3 $}=$ 1080 $}$ 의 고유 세트가 $\textstyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080$ 있다.
집합에 $d$ ${\dapplaystyle d}$ 특성이 $d$ $4-d$ - d $4-d$ {\d $표시style$ 4-d $}$ 특징이 $4-d$ 같을 확률은 $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ ( $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ d ) $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ {\ $dapplaystyle \textstyle {\frac {{4 \선택 d}2^{d}}}{80}}}}}$ 이다 $\textstyle {\frac {{4 \choose d}2^{d}}{80}}$ 참고:두 카드가 동일하지 않기 때문에 d = 0이 불가능한 경우)따라서 가능한 세트의 10%는 하나의 형상에서, 30%는 두 형상에서, 40%는 세 형상에서, 20%는 네 형상에서 각각 다르다.
다른 12 카드 거래의 수는 $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ ( $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ ) $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ = $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ = $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ $\textstyle {81 \choose 12}={\frac {81!}{12!69!}}=70\,724\,320\,184\,700\approx 7.07\times 10^{13}$ ${\$ $}}}=70\724\,320\,1700\,약$ 7 $.07\cH10^{13$
세트 게임을 할 때 12개의 카드에서 세트가 없을 확률은 첫 라운드를 30:1로 시작한다.그리고 나서 그들은 빠르게 떨어지고, 약 4라운드가 끝나면 그들은 14:1이 되고, 다음 20라운드에서는 13:1을 향해 천천히 떨어진다.그래서 대부분의 라운드는 14:1에서 13:1의 확률로 진행된다.^[7]
게임을 할 때 15개의 카드에 Set가 없을 확률은 88:1이다.^[7] (이는 15개의 카드에 Set가 없을 확률은 88:1이다. 왜냐하면 플레이 중에는 12개의 카드에 Set가 없을 때만 15개의 카드가 표시되기 때문이다.)
전체 게임의 약 30%가 12개 카드 중 항상 세트를 가지고 있기 때문에 15개 카드로 갈 필요가 없다.^[8]
The average number of available Sets among 12 cards is $\textstyle {12 \choose 3}\cdot {\frac {1}{79}}\approx 2.78$ and among 15 cards $\textstyle {15 \choose 3}\cdot {\frac {1}{79}}\approx 5.76$ . However, in play the numbers are 더 작은
만약 데크에서 26세트를 골랐다면, 마지막 세 개의 카드는 반드시 또 다른 27세트를 형성할 것이다.

복잡성

속성 수와 값이 다른 세트의 자연적인 일반화를 사용하여, 처리된 카드 모음에서 세트가 존재하는지 여부를 결정하는 것은 NP-완료인 것으로 나타났다.^[9]

참조

^ "How to Play the Daily SET Puzzle". America's Favorite Card Games®. 2015-08-11. Retrieved 2022-02-07.
^ "Set - The history of". 2006-10-21. Archived from the original on 21 October 2006. Retrieved 2022-02-07.
^ "Set Variants". magliery.com. Retrieved 2022-02-07.
^ "Get Set - A Set Variant". www.thegamesjournal.com. Retrieved 2022-02-07.
^ Edel, Yves (2004), "Extensions of generalized product caps", Designs, Codes and Cryptography, 31 (1): 5–14, doi:10.1023/A:1027365901231, MR 2031694, S2CID 10138398.
^ Benjamin Lent Davis and Diane Maclagan. "The Card Game Set" (PDF). Archived from the original (PDF) on June 5, 2013.
^ ^a ^b "SET Probabilities Revisited".
^ "SET® Probabilities Revisited". Henrik Warne's blog. 2011-09-30. Retrieved 2022-02-07.
^ Chaudhuri, Kamalika; Godfrey, Brighten; Ratajczak, David; Wee, Hoeteck (2003). "On the Complexity of the Game of Set" (PDF). {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)

외부 링크

엔터프라이즈 웹 사이트 설정
A(2002년?) 게임 세트 수학 탐구. '세트를 만들지 않고 몇 장의 카드를 놓을 수 있는가'를 비롯해 여러 종류의 세트 게임(일부 파노 비행기 안)에 대한 조사도 포함된다.
카드 게임 세트의 수학 - Paola Y.Reyes - 2014 - Rhode Island College Awards 프로젝트
BoardGameGeek에서 설정
tcl/Tk로 작성된 세트의 그래픽 컴퓨터 카드놀이 버전이 있다.이 스크립트는 ActiveState Ftp://tcl.activestate.com/pub/tcl/nightly-cvs/의 "tclapps" 번들에서 찾을 수 있다.
세트, 행성, 혜성.대체 확장된 세트 버전
일일 퍼즐 설정
SET Finder
친구와 함께 설정

[1] "How to Play the Daily SET Puzzle". America's Favorite Card Games®. 2015-08-11. Retrieved 2022-02-07.

[2] "Set - The history of". 2006-10-21. Archived from the original on 21 October 2006. Retrieved 2022-02-07.

[3] "Set Variants". magliery.com. Retrieved 2022-02-07.

[4] "Get Set - A Set Variant". www.thegamesjournal.com. Retrieved 2022-02-07.

[5] Edel, Yves (2004), "Extensions of generalized product caps", Designs, Codes and Cryptography, 31 (1): 5–14, doi:10.1023/A:1027365901231, MR 2031694, S2CID 10138398.

[6] Benjamin Lent Davis and Diane Maclagan. "The Card Game Set" (PDF). Archived from the original (PDF) on June 5, 2013.

[Revisited-7] "SET Probabilities Revisited".

[8] "SET® Probabilities Revisited". Henrik Warne's blog. 2011-09-30. Retrieved 2022-02-07.

[9] Chaudhuri, Kamalika; Godfrey, Brighten; Ratajczak, David; Wee, Hoeteck (2003). "On the Complexity of the Game of Set" (PDF). {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search

세트(카드 게임)

네임스페이스

더

목차

역사

게임.

세트의 기본 콤비네이터

복잡성

참조

외부 링크