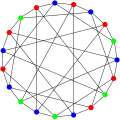
로버슨 그래프

로버슨 그래프
로버트슨 그래프는 해밀턴식이다.
이름을 따서 명명됨	닐 로버트슨
정점	19
가장자리	38
반지름	3
지름	3
둘레	5
자동형성	24(D12)
색수	3
색도 지수	5[1]
책두께	3
대기열 번호	2
특성.	케이지 해밀턴어
그래프 및 모수 표

그래프 이론의 수학적 분야에서, 로버트슨 그래프 또는 (4,5)-케이지는 닐 로버트슨의 이름을 딴 19개의 정점과 38개의 가장자리를 가진 4-정규의 비방향 그래프다.^[2][3]

로버트슨 그래프는 독특한(4,5)-케이지 그래프로 1964년 로버트슨에 의해 발견되었다.^[4]케이지 그래프로는 둘레 5로 가장 작은 4-정규 그래프다.

색도 번호 3, 색도 지수 5, 직경 3, 반지름 3을 가지며, 4버텍스 연결과 4엣지 연결이다.책 두께 3과 줄 2가 있다.^[5]

로버슨 그래프는 해밀턴 그래프로서 5,376개의 뚜렷한 해밀턴 사이클을 가지고 있다.

대수적 특성

로버슨 그래프는 정점 변환 그래프가 아니며 완전 자동모형 집단은 회전과 반사를 모두 포함한 일반 도데카곤의 대칭 집단인 순서 24의 이형성 그룹이다.^[6]

로버트슨 그래프의 특성 다항식은

${\displaystyle (x-4)(x-1)^{2}(x^{2}-3)^{2}(x^{2}+x-5)}$

${\displaystyle (x^{2}+x-4)^{2}(x^{2}+x-3)^{2}(x^{2}+x-1)^{2}(x^{2}+x-1).\ }$

갤러리

• 

  로버트슨 그래프는 원본 출판물에 그려진 것이다.

• 

  로버트슨 그래프의 색수는 3이다.

• 

  로버트슨 그래프의 색지수는 5이다.

참조