완만한 교차로
Relaxed intersectionm 집합의 완화된 교차로는 집합 간의 일반적인 교차로에 해당하지만 빈 교차로를 피하기 위해 소수의 집합을 완화할 수 있습니다.이 개념을 사용하여 소수의 제약 조건을 완화함으로써 일관성이 없는 제약 만족 문제를 해결할 수 있습니다.모수 추정을 위해 경계 오류 접근법을 고려할 때, 완화된 교차로를 통해 일부 특이치에 대해 강건할 수 있다.
정의.
m개의 X, X ({1m의 X_ { ({ X\} =\} }) {} 。}}s( qq 제외).이 정의는 그림 1에 나타나 있습니다.
( ) 카드 { i X i . { displaystyle \ {} \ \ { X _ { i \ right \ } 를 정의합니다.
{ -( [ - , ). { X^ { \ { q \ } = \ ^ { - ( [ m - , m] ) 。
따라서 q완화 교차로를 특징짓는 것은 일련의 반전 문제입니다.[1]
예
8개의 인터벌에 대해 검토합니다. 1 [, , {\ _ { 1 } [ , , { 2} \ [ 2 , , { { } [ , , 7 { } ,
우리는 가지고 있다.
완만한 간격 교차로
완화된 구간 교차는 구간이 아닙니다.따라서 결과의 간격 선체를 취합니다.i가 간격인 완만한 교차는 Marzullo 알고리즘을 사용하여 m.log(m)의 복잡도로 계산할 수 있습니다.to { displaystyle \ 를 나타내는 m 간격의 하한과 상한을 모두 정렬하면 충분합니다. 그러면 쉽게 세트를 얻을 수 있습니다.
간격의 합성에 해당합니다.그런 다음 이 결합을 포함하는 최소 간격을 반환합니다.
그림 2는 위의 예와 관련된 (x ) \ \ )를 나타내고 있습니다.
완만한 박스 교차로
n{\n의 m박스의 q완화 교차를 계산하기 위해 n축에 대해 모든 m박스를 투영한다.m 구간의 n개 그룹 각각에 대해 q-완화 교차를 계산한다.결과 간격 n개의 데카르트 곱을 반환합니다.[2] 그림 3은 6개의 상자의 4완완화 교차로를 보여줍니다.빨간색 상자의 각 점은 6개 상자 중 4개에 속합니다.
릴랙스 유니언
1, (\ X_의 q완화 결합은 다음과 같이 정의됩니다.
q=0일 때 이완 결합/교차는 고전 결합/교차에 해당합니다.좀 더 정확히 말하면
그리고.
드 모르간의 법칙
X가 X_의 세트인 ,
결과적으로
계약자의 완화
1, { \을 m {1}, \m의 계약자로 합니다.
{ q { X^ { \ { q \} } for 。
는 X { q {\ {{\{의 계약자입니다.
청부업자
SIDIA(Set Inversion Via Interval Analysis) 등의 분기 및 경계 알고리즘과 조합하여 n R의 m개 서브셋의 q완화 교차를 계산할 수 있습니다.
제한 오류 추정에 적용
q완화 교차로는 견고한 현지화[4] 또는 트래킹에 사용할 수 있습니다.[5]
견고한 관찰자는 특이치에 대해 견고하기 위해 완화된 교차로를 사용하여 구현될 수도 있다.[6]
우리는 여기에 그 방법을 설명하기 위한 간단한 예를 제안한다.ih 모델의 출력이 다음과 같이 주어진 모델을 고려합니다.
서 p 2 (\ p R )는 다음과 같습니다.
서t\i}및 [ i {i]}는 다음 목록으로 지정됩니다.
q\^{- 세트 -1 ()를 그림 4에 나타냅니다.
레퍼런스
- ^ Jaulin, L.; Walter, E.; Didrit, O. (1996). Guaranteed robust nonlinear parameter bounding (PDF). In Proceedings of CESA'96 IMACS Multiconference (Symposium on Modelling, Analysis and Simulation).
- ^ Jaulin, L.; Walter, E. (2002). "Guaranteed robust nonlinear minimax estimation" (PDF). IEEE Transactions on Automatic Control. 47.
- ^ Kieffer, M.; Walter, E. (2013). Guaranteed characterization of exact non-asymptotic confidence regions in nonlinear parameter estimation (PDF). In Proceedings of IFAC Symposium on Nonlinear Control Systems, Toulouse : France (2013).
- ^ Drevelle, V.; Bonnifait, Ph. (2011). "A set-membership approach for high integrity height-aided satellite positioning". GPS Solutions. 15 (4).
- ^ 를 클릭합니다Langerwisch, M.; Wagner, B. (2012). "Guaranteed Mobile Robot Tracking Using Robust Interval Constraint Propagation". Intelligent Robotics and Applications..
- ^ Jaulin, L. (2009). "Robust set membership state estimation ; Application to Underwater Robotics" (PDF). Automatica. 45: 202–206. doi:10.1016/j.automatica.2008.06.013.
- ^ Jaulin, L.; Kieffer, M.; Walter, E.; Meizel, D. (2002). "Guaranteed robust nonlinear estimation, with application to robot localization" (PDF). IEEE Transactions on systems, man and cybernetics; Part C Applications and Reviews. 32. Archived from the original (PDF) on 2011-04-28.






![{\displaystyle X^{\{q\}}=\lambda ^{-1}([m-q,m]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a061a3400e3891d6b2019b6f5577398e3af8766)
![{\displaystyle X_{1}=[1,4],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af99892b7ed95bc8b01972b7be903134c2cba0f6)
![{\displaystyle X_{2}=\ [2,4],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9531f6c8b6ff361af716c5c8155d0cd3007425b)
![{\displaystyle X_{6}=[3,7].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/562b9e580672a7c75318ac96a7995ec3fab13587)

![{\displaystyle X^{\{1\}}=[3,4],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7928014128a53893e7d057601d027b84c9f9a0b)
![{\displaystyle X^{\{2\}}=[3,4],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80dac0757559626654549f071041b301a8f90621)
![{\displaystyle X^{\{3\}}=[2,4]\cup [6,7],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ece0be4f2d5a10db46776a9c106ca65b79b96d4)
![{\displaystyle X^{\{4\}}=[2,7],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3fc1592c25b36e319d639b0f5b52fb1e7b885fc)
![{\displaystyle X^{\{5\}}=[1,9],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48f7fda52531e256cee2b6d9440d64ce21be8dae)
![{\displaystyle X^{\{6\}}=]-\infty ,\infty [.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd443cc01f235d00232b0e04e637bff1a3f723b5)

![{\displaystyle X^{\{q\}}=\lambda ^{-1}([m-q,m])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/294b77be8504fee0a62cbc855b66de2badd9b759)
 나타내고 있습니다.
나타내고 있습니다. 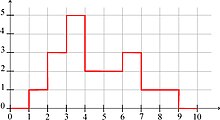









![{\displaystyle C([x])=\bigcap ^{\{q\}}C_{i}([x]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788587729f7e8ca9fb9fe1fdd1102cecdc2a0f1d)

![{\displaystyle {\overline {C}}([x])=\bigcap ^{\{m-q-1\}}{\overline {C}}_{i}([x])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d59a6070cd4b8efebd4b14a71f7d2d0497ae2d7b)





![{\displaystyle f_{i}(p)\in [y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64f73d68f14eabca9ecdda9f468cc96106ecc7bd)

![{\displaystyle [y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0733aa435bd20b12b259b38350ab7b3e2bd2a9d)
![{\displaystyle \{(1,[0;0.2]),(2,[0.3;2]),(3,[0.3;2]),(4,[0.1;0.2]),(5,[0.4;2]),(6,[-1;0.1])\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eefb2caf9e7b28cf4e0a7f3c3f7a3524bc186ba7)



