최대 흐름 문제

최적화 이론에서 최대 흐름 문제는 가능한 최대 흐름 속도를 얻는 흐름 네트워크를 통해 실현 가능한 흐름을 찾는 것입니다.

최대 흐름 문제는 순환 문제 등 보다 복잡한 네트워크 흐름 문제의 특수한 경우로 볼 수 있습니다.s-t 흐름의 최대값(즉, 소스 s에서 싱크 t로의 흐름)은 max-flow min-cut 정리에 기술된 바와 같이 네트워크 내의 s-t 컷(즉, s를 t에서 절단)의 최소 용량과 동일합니다.

역사

최대 흐름 문제는 1954년 T. E. Harris와 F. S. Ross에 의해 소련 철도 교통 ^[1][2][3]흐름의 단순화된 모델로 처음 공식화되었습니다.

1955년, 레스터 R. 포드 주니어와 델버트 R. 풀커슨은 최초로 알려진 알고리즘인 포드-풀커슨 ^[4][5]알고리즘을 만들었다.Ford와 Fulkerson은 1955년 ^[4]논문에서 Harris와 Ross의 문제는 다음과 같이 공식화된다고 썼다(5페이지^[1] 참조).

여러 중간 도시를 통해 두 도시를 연결하는 철도 네트워크를 고려해 보십시오. 여기서 네트워크의 각 링크에는 용량을 나타내는 번호가 할당됩니다.정상 상태라고 가정할 때, 한 도시에서 다른 도시로 최대 흐름을 찾습니다.

1962년 Ford와 Fulkerson은 Flows in ^[5]Network라는 책에서 다음과 같이 썼습니다.

1955년 봄, General F. S. Ross (Ret.)와 함께 철도 교통 흐름의 단순화된 모델을 공식화했고, 이 특별한 문제를 모델에 의해 제안된 중앙 문제로 지목한 T. E. Harris가 저자들에게 제시하였습니다 [11].

여기서 [11]은 1955년 Harris와^[3] Ross에 의한 철도망 용량 평가 방법의 기초 (페이지^[1] 5 참조)를 참조합니다.

수년간 최대 흐름 문제에 대한 다양한 개선 솔루션이 발견되었는데, 특히 Edmonds와 Karp와 독립적으로 최단 증강 경로 알고리즘, Dinitz의 블로킹 흐름 알고리즘, Goldberg와 Tarjan의 푸시 릴라벨 알고리즘, Goldberg와 Rao의 바이너리 블로킹 흐름 알고리즘 등이 발견되었다.Sherman과 Kelner, Lee, Orecchia 및 Sidford의 ^[7][8]알고리즘은^[6] 각각 대략적으로 최적의 최대 흐름을 찾지만 방향성이 없는 그래프에서만 작동합니다.

2013년 제임스 B. Orlin은 O${\displaystyle }$( ${\displaystyle VE}$ $)\$^[9]$displaystyle$O ( V E$$)$알고리즘$에 관한 논문을 발표했습니다.

2022년 리첸, 라스무스 경, 양 P.${\displaystyle {}^{\mathrm{}}}$, Richard Peng, Maximilian Probst Gutenberg 및 Sushant Sachdeva는${\displaystyle {}^{}}$O ( $E$ 1 +${\displaystyle {\mathrm{o}}^{}}$ (${\displaystyle {}^{}}$1 $){$ $display style$O ( E$^ 1$ + o (1$)$^[10][11] )로 실행되는 거의 선형 시간 알고리즘을 발표했습니다.

정의.

먼저 몇 가지 표기법을 설정합니다.

• N ${\displaystyle =}$ (${\displaystyle V}$ ,${\displaystyle E}$) { $displaystyle$ N = ($V$ , E )$$${\displaystyle \}}$ 를$$N { $displaystyle$ N$}$ 의 $소스$ 및 싱크로서 각각 t${\displaystyle v}$V { $displaystyle$s , $t$\ $in$ V$$} 를 사용하는$$ $네트워크$라고 $합니다{\displaystyle }$.
• g$(\$$displaystyle$$$g)가$$N(\$displaystyle$ N$)$의 가장자리에서 기능하는 $경우{\displaystyle }$ (${\displaystyle u,}$ ${\displaystyle v)}$ ${\displaystyle e}$E$(\displaystyle (u$$,$ $v$${\displaystyle )\backslash }$$in$ E$)$의${\displaystyle }$값은 ${\displaystyle {\mathrm{gu}}_{}}$ v$(\$$displaystyle$ $g_$${$$uv$}) $또는$ g$u$ $v)$로 표시됩니다$.$$}$

정의.에지의 용량은 에지를 통과할 수 있는 최대 흐름량입니다.공식적으로는 $지도{\displaystyle }$ c${\displaystyle :}$ ${\displaystyle E}$ ${\displaystyle \to {}^{}}$+$$. {$displaystyle$ c$:$$E\to \mathbb {R}^{+}.$$}$

정의.흐름은 $맵{\displaystyle f}$ : E ${\displaystyle \to }$ {\$displaystyle$ f$:$$다음$ 조건을 $충족$하는 E$\to$\mathbb {$R} }$입니다.

• 용량 제약엣지의 흐름은 용량을 초과할 수 $없습니다{\displaystyle {}_{}}$.${\displaystyle {즉}_{}}$, fu ${\displaystyle v_{}}$} ${\displaystyle {}_{}}$ v \ $displaystyle f_$${uv$$}$ \leq $c_{uv$} for$$${\displaystyle }$all ( ${\displaystyle u}$,${\displaystyle v}$ )${\displaystyle }$e${\displaystyle E}$. \ $displaystyle$ ($u$ , v ) \ $in$ E .
• 흐름의 보존노드에 들어가는 흐름의 합계는 송신원과 싱크를 제외하고 해당 노드에서 나가는 흐름의 합계와 같아야 합니다.또는 다음 중 하나를 선택합니다.

$\displaystyle \forall v\in V\s,t\:\sum \sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}.}$

비고. 흐름은 스큐 $대칭$입니다.f ${\displaystyle u_{}}$ v $=$ - $f$ ${\displaystyle v_{}}$u { $displaystyle$ f$_${ $uv }$ ${\displaystyle \mathrm{e<img\; alt="\{\backslash displaystyle\; f\_\{uv\}=-f\_\{vu\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/57af4d8537ee892330f4fdcdeb91623bff33f441"\; style="vertical-align:\; -0.671ex;\; width:11.125ex;\; height:2.509ex;">}\}}$ E$$. \ $displaystyle ( u$ , ${\displaystyle v}$ \ $in$ E$$}

정의.흐름의 값은 소스로부터 싱크까지 통과하는 흐름의 양입니다.$흐름{\displaystyle }$f : ${\displaystyle E}$ ${\displaystyle \to {\mathbb{}}^{}}$+ \ $displaystyle$ f$$:$E\to$\mathbb {$R}^{+}$는 다음과 같이 표시됩니다.

${\displaystyle f =\sum _{v:(s,v)\in E}f_{sv}}$

정의.최대 흐름 문제는 소스로부터 싱크까지 가능한 한 많은 플로우를 라우팅하는 것입니다.즉, $플로우{\displaystyle {}_{}}$ ${\displaystyle {\text{fmax}}_{}}${\$display$ style $f_{\textrm {max}}$를 최대값으로 찾는 것입니다.

최대 흐름은 여러 개 존재할 수 있습니다.또한 흐름의 임의의 실수(또는 임의의 합리적) 값이 (정수가 아닌) 허용될 경우 베이스 최대 흐름의 선형 조합이 무한히 많기 때문에 정확히 1개의 최대 흐름 또는 무한히 많은 흐름 중 하나가 존재합니다.즉 u{\displaystyle u}에 대한 또 다른 최대 유량에 흐름 자료는 x, x가장자리 u{\displaystyle u}에 최대 유량의 흐름, 그리고 베의{\displaystyle)}대 보내{\displaystyle y>^}대였기 때문에 각 Δ 우리는 x+Δ{\displayst 보낼 수 있[0, y−)]{\displaystyle \Delta \in[0,y-x]}∈.yle)$+\Delta }$유닛을$$$$ $사용$하여 나머지 에지에 플로우를 적절히 라우팅하여 다른 최대 플로우를 얻을 수 있습니다.흐름 값이 임의의 실수 또는 유리수일 경우 각 쌍 $x{\displaystyle ,}$ $,$ \$displaystyle$$$x$,$$y$에 대해 이러한 $\delta {\displaystyle \mathrm{}}$ $\delta }$ 값이$$ 무한히 존재합니다.

알고리즘

다음 표에 최대 흐름 문제를 해결하기 위한 알고리즘을 나타냅니다.

방법	복잡성	묘사
선형 프로그래밍		법적 흐름의 정의에 의해 주어지는 제약.여기서 선형 프로그램을 참조하십시오.
포드-펄커슨 알고리즘	$(\displaystyle O(E\vert f_{max}\vert)}$	잔차 그래프를 통과하는 열린 경로가 있는 한 경로 상의 최소 잔차 용량을 전송합니다. 알고리즘은 모든 가중치가 합리적일 경우에만 종료가 보증됩니다.이 경우 각 단계에서 흐름에 추가된 양은 가중치의 최소 공통 약수입니다.그렇지 않으면 알고리즘이 최대값으로 수렴되지 않을 수 있습니다.다만, 알고리즘이 종료하면, 반드시 최대치를 찾아낼 수 있습니다.
에드먼즈-카르프 알고리즘	${\displaystyle O(VE^{2})}$	Ford-Fulkerson의 전문화. 너비 우선 검색으로 확대 경로를 찾습니다.
다이닉 알고리즘	${\displaystyle O(V^{2}E)}$	각 단계에서 알고리즘은 잔차 그래프에서 너비 우선 검색을 통해 계층형 그래프를 구축합니다.레이어드 그래프의 최대 흐름은 O$(V$ E$)$ 시간(\$displaystyle$ O$($))으로 계산할 수 있으며, 최대 단계 ${\displaystyle \mathrm{수}}$는$$V${\displaystyle }$- 1(\$displaystyle V-1$입니다.유닛 용량이 있는 네트워크에서는 Dinic 알고리즘은 O${\displaystyle (min}${ ${\displaystyle {}^{2\mathrm{}}}$ /${\displaystyle {}^{}{}^{}}$, ${\displaystyle {E\mathrm{}1\mathrm{}}^{}}$ / 2$$로$끝납니다.$
MKM(Malhotra, Kumar, Maheshwari) 알고리즘[12]	${\displaystyle O(V^{3})}$	블로킹 플로우를 구성하는 다른 접근방식을 사용한 Dinic 알고리즘의 수정.원래의 용지를 참조해 주세요.
동적 트리를 사용하는 Dinic 알고리즘	${\displaystyle O(VE\log V)}$	다이내믹 트리 데이터 구조에 의해 레이어 그래프 내의 최대 흐름 계산 속도가${\displaystyle }$O(${\displaystyle V}$ E log${\displaystyle )}$ ${\displaystyle V}$)(\$displaystyle O(VE\log$ V$))$로 향상됩니다.
일반 푸시-릴라벨 알고리즘[13]	${\displaystyle O(V^{2}E)}$	푸시 릴라벨 알고리즘은 프리플로우, 즉 정점에서 초과 가능성이 있는 플로우 함수를 유지합니다.알고리즘은 양의 초과가 있는 정점, 즉 그래프의 활성 정점이 있는 동안 실행됩니다.푸시 조작은 잔류 에지의 흐름을 증가시키고, 정점의 높이 함수는 잔류 에지의 흐름을 푸시할 수 있는 범위를 제어합니다.높이 기능은 라벨 다시 붙이기 조작에 의해 변경됩니다.이러한 동작의 적절한 정의에 의해 결과 흐름 함수가 최대 흐름임을 보증합니다.
FIFO 정점 선택[13] 규칙을 사용한 푸시-릴라벨 알고리즘	${\displaystyle O(V^{3})}$	항상 가장 최근에 활성화된 정점을 선택하고 초과가 양수이고 이 정점에서 허용 가능한 잔류 에지가 있는 동안 푸시 연산을 수행하는 푸시 릴라벨 알고리즘 변형입니다.
최대 거리 정점 선택[14] 규칙을 사용한 푸시-릴라벨 알고리즘	$({displaystyle O(V^{2}{\sqrt {E}})})$	push-relabel 알고리즘의 변형으로, 항상 s$\displaystyle$s $또는$ t$\$$displaystyle$t에서 가장 먼 정점(즉, 가장 높은 라벨 정점)을 선택하지만 그 이외의 경우에는 FIFO 알고리즘으로 진행됩니다.
동적[13] 트리를 사용한 푸시 릴라벨 알고리즘	${\displaystyle O\left(VE\log {V^{2}}{E}}\right)}$	알고리즘은 높이 함수와 관련하여 잔차 그래프에 제한된 크기의 트리를 작성합니다.이러한 트리는 다단계 푸시 작업을 제공합니다. 즉, 단일 에지 대신 전체 포화 경로를 따라 푸시합니다.
KRT(King, Rao, Tarjan) 알고리즘[15]	${\displaystyle O\left(VE\log _{\frac {E}{V\log V}}V\right)}$
바이너리 블로킹플로우[16] 알고리즘	$\displaystyle O\left(E\cdot\min\){V^{2/3}, E^{1/2}\}\cdot \log {frac {V^{2}}{E}}\cdot \log U\right}$	U 값은 네트워크의 최대 용량에 해당합니다.
James B Orlin의 + KRT(King, Rao, Tarjan) 알고리즘[9]	${\displaystyle O(VE)}$	Orlin 알고리즘은 E ${\displaystyle {}^{}}$ O${\displaystyle （}$ V ${\displaystyle {\frac{16}{}}^{}}$ 15 -$$${\displaystyle {}^{}}$- ${\displaystyle O^{}}$ （ \ $display$ $style$ $O$） display$$ O${\displaystyle }$${\displaystyle （}$ \ frac {$16 }$ { $15$} - \ $epsilon }$의 $최대{\displaystyle }$ 흐름 $시간$을 O （ V E$$）로 해결합니다${\displaystyle .}$
캐추리아-리우-시드포드 알고리즘[17]	${\displaystyle E^{4/3+o(1)}U^{1/3}}$	$내부$ 포인트 방식 및 $표준 플로우$를 사용한$$엣지 부스트$.$$런타임{\displaystyle \stackrel{}{}}$O${\displaystyle }$~ ( ${\displaystyle {}^{}}$ ${\displaystyle {10}^{}}$/ ${\displaystyle {}^{}{}^{}}$ U${\displaystyle {1\mathrm{}}^{}}$ /${\displaystyle {}^{}{7\mathrm{}}^{}}$) {$display$ { $tilde${$O$} （ E $^$ { $10$/ 7 } U^ {$1$ / 7$$}$$[18]} }}을 달성한 Madry의 이전 알고리즘을 기반으로 합니다.
BLNPSSW/BLLSSSW 알고리즘[19] [20]	${\displaystyle {O}}((E+V^{3/2})\log U)}$	팽창기 분해에 따른 전기 흐름의 내부 포인트 방법 및 동적 유지관리.
가오류펑 알고리즘[21]	${{displaystyle {O}}(E^{\frac {3}{2}}-{\frac {1}{328}}}\log U)}$	Gao, Liu 및 Peng의 알고리즘은 [Mdrydry JACM '16]의 내부 포인트 방법 기반 알고리즘의 핵심에서 증가하는 전기 흐름을 동적으로 유지하는 것을 중심으로 한다.여기에는 제한된 설정에서 저항 업데이트가 진행 중인 그래프에서 큰 전기 에너지로 에지를 반환하는 데이터 구조를 설계해야 합니다.
Chen, Kyng, Liu, Peng, Gutenberg 및 Sachdeva 알고리즘[10]	$(\displaystyle O(E^{1+o(1)}\log U)}$	Chen, Kyng, Liu, Peng, Gutenberg 및 Sachdeva의 알고리즘은 ${\displaystyle {\mathrm{E1}}^{}}$+$o ( )$의 시퀀스를 통해 플로우를 구축함으로써 최대 플로우와 최소 코스트 플로우를 거의 선형 시간 내에 해결합니다$($$각각각$은 ${\displaystyle {디스플레이}^{}}$1에서 계산 및 상각됩니다$).$$E^{o(1)}}$ 동적$$ 데이터 구조를 사용한 시간.

그 외의 알고리즘에 대해서는, Goldberg & Tarjan(1988)을 참조해 주세요.

적분 흐름 정리

적분 흐름 정리는 다음과 같이 기술한다.

플로우 네트워크의 각 에지가 적분 캐퍼시티를 가지는 경우, 적분 최대 플로우가 존재합니다.

이 주장은 흐름의 값이 max-flow min-cut 정리로부터 직접 이어지는 정수일 뿐만 아니라 모든 에지의 흐름이 적분하다는 것입니다.이것은 많은 조합 어플리케이션(아래 참조)에 있어서 매우 중요합니다.이 어플리케이션에서는, 에지를 통과하는 플로우가, 그 에지에 대응하는 항목을 검색 세트에 포함할지를 부호화할 수 있습니다.

어플

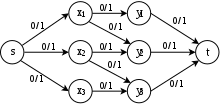
멀티 소스 멀티 싱크의 최대 흐름 문제

$네트워크{\displaystyle }$ $N{\displaystyle }$ ${\displaystyle =}$ (${\displaystyle V}$ ,${\displaystyle E}$) \ $displaystyle$ N$$$=$ (${\displaystyle }$$V$ ,${\displaystyle {}_{}}$$$) \ displaystyle $S$ { ${\displaystyle {s\mathrm{}}_{}}$1, $...$ , s $n$} { $displaystyle$ S = \ { s _ {1} , \$ldots$ , s _ n $}$ $displaydisplaydisplaydisplay$ = { ${\displaystyle {}_{}{}_{}{}_{}}$,${\displaystyle }$. t $style$ }$$$${\$displaystyle$ N$}.$ $S$의 각 $정점$에$연결$된 $통합$ 소스 및$T의$각 정점에 의해 연결된 통합 싱크(일명 슈퍼소스 및 슈퍼싱크)$$를 각 에지에 무한 용량으로 추가하여 멀티소스 멀티싱크 문제를 최대 흐름 문제로 전환할 수 있습니다$.$(제4-1-1 그림 참조).

초당 최대 카디널리티 일치

${\displaystyle \mathrm{초당}}$ $그래프{\displaystyle }$ G ${\displaystyle =}$ ( X${\displaystyle y}$Y ,${\displaystyle E}$) { $displaystyle$ G = ($X$ \ $cup$Y , $E$)$$} a 、$$G \ $displaystyle$ G$$} 에서의 최대 카디널리티 일치를 구합니다.이것은 가능한 가장 많은 에지를 포함하는 일치입니다.이 문제는 네트워크 $N{\displaystyle }$ ${\displaystyle =}$ ( ${\displaystyle Xy}$ Y ${\displaystyle \cup }${ s , t${\displaystyle }$} , $){$ $display$ N = ($X$ \ $cup$Y \ $cup$\ {$s$ , $t$\ , $E$' $)$를 구축함으로써 최대 흐름 문제로 변환할 수 있습니다.

1. ${\displaystyle E^{}}$ ${\$ { $display style$ E$$} 에는$$ X$(style$ X)에서 Y$($style$$ Y$)$로 향하는 G$($$display$ $style$ G$)$ $엣지$가 포함되어 있습니다.
2. ${\displaystyle (}$ ${\displaystyle s}$,${\displaystyle x}$ )${\displaystyle {}^{}}$ $、$ 각 $x$${\displaystyle x}$X$$\ $displaystyle$($s$ ,$x$ ) \ $in$ E$'$${\displaystyle {}^{}}$ ( ( ( X$$each ( ( ( ( ( ${\displaystyle y}$, ${\displaystyle t}$) ${\displaystyle 、}$ e Y$$ [$$\ $displaystyle$($y$ ,$t$ ) \ $in$ $E$$'$ 。
3. ${\displaystyle }$$c{\displaystyle }$${\displaystyle }$(${\displaystyle e}$ ) ${\displaystyle =}$ e ${\displaystyle \in }$ $′$ { $displaystyle$c ( e ) $$$= 1$ ($그림$ 4.3.1 $참조$).

다음으로 N$(\displaystyle$ N$)$의 최대 흐름 값은 G$(\displaystyle$ G$)$의 최대 일치 크기와 같으며, 최대 카디널리티 매칭은 flow 1$(\displaystyle$ 1)을$$일체형 max-flow에 갖는 에지를 취함으로써 찾을 수 있습니다.

방향 비순환 그래프의 최소 경로 커버

방향 비순환 $그래프{\displaystyle }$ G ${\displaystyle =}$ (${\displaystyle }$V ,${\displaystyle E}$) { $displaystyle$ G = ($V$ , $E$) } a$$、 V$$}$$$v$、 V ′${\displaystyle {}^{}}$、 V ′ 、 V $in{\displaystyle {}^{}}$ （ \ $display$ ） ${\displaystyle =}$ = $=$ ( $V$ ${\displaystyle {}^{}}$ ${\displaystyle {\cup }_{}}$ ${\displaystyle {\text{V}}_{}}$ in${\displaystyle {}_{}}$E${\displaystyle {）}^{}}$ $style$ G （ \ displaystyle ）$$。$(\displaystyle$ G$),$ 여기서

1. ${\displaystyle V_{\textrm {out}}=\{v_{\textrm {out}\mid v\in V\land v\text{에는 발신 에지가 있습니다.}}\}$
2. ${\displaystyle V_{\textrm {in}}=\{v_{\textrm {in}}\mid v\in V\land v\text{에지(s)}}\}}$
3. ${\displaystyle E^{}}$ ${\displaystyle {\prime }^{}}$ ${\displaystyle =}${ ( ${\displaystyle {\text{u}}_{}}$out , ${\displaystyle {}_{}{\text{in}}_{}}$ )${\displaystyle v}$ ${\displaystyle V_{}}$ ${\displaystyle o_{}}$ t${\displaystyle {}_{}}$× ${\displaystyle V_{}}$ ${\displaystyle i_{}}$ n$u$ ,$v$ )${\displaystyle e}$ E $}$ = \ { $display style$ E' = \ { \$textrm { in }$ \ $in$ V _ {$out$} \ $times$ V _ { $in$} \ $mid U$}$$。

그러면 G$({displaystyle$ G$}$가 m개의 ${displaystyle$ m$}$개의$$ 모서리와${\displaystyle }$$n-m$의$경로$를 $포함$하는 정점 분리 경로 $커버{\displaystyle }$C({$displaystyle$ C$})$를 가지고 $있는{\displaystyle }$ 경우에만 G$({$ G$')$가$$m({$displaystyle$m$$}) $크기$의$M$({$displaystyle$M)을$$ 가지고 $있음$을 알 수 있습니다$.$\$displaystyle$n은$$ G$(\displaystyle$ G$)$의 정점수이므로 G$(\$ G$')$의 최대 카디널리티 매칭을 찾는 것으로 문제를 해결할 수 있습니다$.$

직관적으로 두 개의 $꼭지점{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{u}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ t${\displaystyle {,}_{}}$ $vi$$$n {\$displaystyle u_{\mathrm {out}}, v_${\mathrm {in$}}$이$($가) M {\$displaystyle$ M$}$에서 일치할 경우${\displaystyle \mathrm{모서리}(}$u$,$ v$)$는$$C {$displaystyle$ C$}$에 $포함$됩니다.\$displaystyle$ C의 $가장자리{\displaystyle }$ 수는 $분명$합니다.C$${\$displaystyle$ C$}$가 정점분리임을 확인하려면 다음 사항을 고려하십시오.

1. G ${\$ {$$\ $display style$ G$$} {\ $の$ $v{\displaystyle {}_{}}$ v v v $_${ \ $textrm${$out$} v$$$$M { $display style$ M$$} 에서는 일치하지 않을 수 있습니다.이 경우 C$${ \ $display style$ C$$} 에서는$$v$${ $display$ $style$v } leaving$$ v $v{\displaystyle }$ v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v v$C$ {\$displaystyle$ C$\}$의 $yle$ v$.$ 어느 경우든 C$${\$displaystyle$ C$\}$의 $정점{\displaystyle }$v {\$displaystyle$ v$}$를 남기는 가장자리는 1개뿐입니다.
2. 마찬가지로 G ${\$ { { \ $displaystyle$G } $$$g$ の \ $displaystyle$ v _ { \$textrm$ { in$}$ の $v{\displaystyle {}_{}}$ if v in ${\displaystyle {\text{inV}}_{}}$에 일치하는 경우는 C$${ \ $displaystyle$ C$$}의 v$${ \ $displaystyle$v$$}에 단일 착신 에지가 존재합니다.$그렇지{\displaystyle }$ 않은 경우는$$C ${\$ $displaystyle$ C$$}의 착신 에지가 없습니다.

따라서 어떤 꼭지점 이는 C{C\displaystyle}의 모든 경로vertex-disjoint 있다는 것을 의미해 C{C\displaystyle}, 2 들어오는 또는 2대 가지고 있다.

는 표지 C{C\displaystyle}n− m{\displaystyle n-m}size 한다는 사실을 보여 주기 위해, 우리는 빈 커버와 점진적으로 그것을 짓기 시작한다.표지에 향점 u{\displaystyle u}을 추가하려면 역시 기존 경로에, 길이 또는 0인 새로운 길 그 꼭지점에서 시작하여 만들어 추가할 수 있습니다.때마다 양쪽(u, v)∈ E{\displaystyle(u,v)\in E}과 표지에 어떤 경로 v{\displaystyle v}, 또는(v마)∈ E{\displaystyle(v,u)\in E}그리고 v{\displaystyle v}에서 약간의 경로 끝에 그 전자의 경우 적용된다.후자의 경우 항상 적용된다.전자의 경우는 모서리의 커버에 있는지 1에서 경로의 번호가 그대로 유지되는 한, 후자의 경우 경로의 번호와 가장자리의 수가 같은 stays 증가한다 증가한다.이제 모든 n{n\displaystyle}vertices을 덮은 뒤 하는 행동은 길과 모서리의 표지에 그 숫자의 합은 n{n\displaystyle}분명하다.그러므로 만약 가장자리의 표지에 번호는 결제{m\displaystyle}, 경로의 번호는 n− m{\displaystyle n-m}.

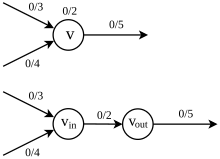
정점 용량으로 최대 흐름

${\displaystyle N}$ $=$ ( V${\displaystyle }$,${\displaystyle E}$) {$displaystyle$ N=($V, E)}$을(를) 네트워크로 $합니다{\displaystyle }$.각 노드에 에지 용량 외에 용량이 있다고 가정합니다. 즉, $매핑{\displaystyle }$ c${\displaystyle :}$ ${\displaystyle V}$ ${\displaystyle \to {}^{}}$+ ,$${\$displaystyle$ c$:$$흐름{\displaystyle }$f {\$displaystyle$ f$}$가 흐름의 용량 제약 및 보존뿐만 아니라 정점 용량 제약도 충족해야$하는$ V$\to$\mathbb {$R}$^{+}

$\displaystyle \sum _{i\in V}f_{iv}\leq c(v)\qquad \forall V\backslash \{s,t\}.}$

즉, 정점을 통과하는 흐름의 양은 정점의 용량을 초과할 수 없습니다.N$(\displaystyle$ N$)$을 $통과$하는 최대 흐름을 구하려면 N$(\displaystyle$ N$)$을 확장하여 문제를 원래 의미의 최대 흐름 문제로 변환합니다. 먼저 각 $(\$$displaystyle$$$$v_{\text{in}}})$는 v(\$displaystyle v_{\text$로$$됩니다.$여기$서 {\$displaystyle v_{\text{$in$}}$의 v는$$v {\$displaystyle$v}로 들어가는 에지로 $연결$되고, ${\displaystyle {\text{v}}_{}}$out {\$displaystyle$ $v_$${\text$${$$out$$}}$는$$v$$ {$displaystyle$ v$\}$에서$$ 에지로 연결된 $용량{\displaystyle {}_{}}$ c$($ $)$를 $할당$합니다.$ext{in}}$ $및$ ${\displaystyle {\text{vout}}_{}}${$style v_{\text{out}}($그림 4.4.1 참조).이 확장 네트워크에서는 정점 용량 제약이 제거되므로 이 문제는 원래의 최대 흐름 문제로 취급할 수 있습니다.

에서 t까지의 최대 패스 수

방향 $그래프{\displaystyle }$ G ${\displaystyle =}$ ( ${\displaystyle V}$,${\displaystyle E}$) { $displaystyle$ G = ($V$ , $E$) 、 2개의 $꼭지점{\displaystyle }$s { \ $displaystyle$ $s{\displaystyle }$$$}$$$、$$$$t$ { $displaystyle$ t$$}에서 t { $displaystyle$ t$$}까지의 최대 경로 수를 구합니다.이 문제에는 몇 가지 종류가 있습니다.

1. 경로는 에지 분리되어야 합니다.이 문제는 G$({displaystyle$ G$\}$로부터 네트워크 $N{\displaystyle }$ $=$ ($V,$ $)$를 구축하고, 각각 $s(\displaystyle$s$$)와 t$(\displaystyle$ t$)$를 N$(\displaystyle$ N$)$의 소스 및 싱크로서 각 엣지 용량을 1로 할당함으로써 $최대{\displaystyle \mathrm{}}$ 흐름 문제로 변환할 수 있습니다.$$\$displaystyle$ 1$.$ 이 네트워크에서는$$k \$displaystyle$ k \displaystyle k$$엣지$$ 분리 경로가 있는 경우 최대 $흐름$은 k \$displaystyle$k 입니다$.$

2. 패스는 독립적이어야 합니다.즉, 정점분리(s$\displaystyle$ s$$$)$$및{\displaystyle }$ t$\displaystyle$t $$$제외{\displaystyle }$).정점 용량을 가진 ${\displaystyle G(\{}$$displaystyle$ G$})$로부터 $네트워크{\displaystyle }$ N $=$ (${\displaystyle V,}$ E$)$ ({$displaystyle$ N=($V, E)}$을 구성할 수 있습니다. 여기서 모든 정점과 모든 가장자리의 용량은$$1({$displaystyle$$$1)입니다$.$ $그러면$$$최대 흐름의 값은 s에서 $tdi$까지의$$독립 경로의 최대 수와 동일합니다.$splaystyle$ t$\}$ 입니다.

3. 경로의 엣지 분리 및 정점 분리 외에 경로의 길이 제약도 있습니다.정확히 k\$displaystyle$ k$\backslash$$또는$ 최대$$k\$displaystyle$k$\backslash .$ 이 문제의 대부분의 변형은 k$\displaystyle$ k$\}$^[22]의 $작은{\displaystyle }$ 값을 제외하고 NP-complete입니다.

폐쇄 문제

유향 그래프의 닫힘은 모서리가 C를 벗어나지 않도록 정점 C의 집합입니다.폐쇄 문제는 정점 가중 유도 그래프에서 최대 가중치 또는 최소 가중치 폐쇄를 찾는 작업이다.최대 흐름 문제를 줄여 다항식 시간으로 해결할 수 있습니다.

실제 응용 프로그램

야구 엘리미네이션

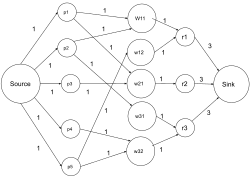
야구 탈락 문제에서는 한 리그에 n개 팀이 출전한다.리그_i 시즌의 특정 단계에서 w는 승리 수, r은_i 팀 i에서 남은 경기 수, r은_ij 팀 j와의 남은 경기 수이다.한 팀은 애초에 시즌을 마칠 기회가 없으면 탈락한다.야구 탈락 문제의 과제는 시즌 중 어느 팀이 탈락할지를 결정하는 것이다.Schwartz는^[23] 이 문제를 최대 네트워크 흐름으로 줄이는 방법을 제안했습니다.이 방법에서는 팀k가 삭제되었는지 여부를 판단하기 위해 네트워크가 작성됩니다.

G = (V, E)를 각각 s,t µ V가 소스 및 싱크인 네트워크로 한다.하나는 게임 노드_ij(이 두 팀 간의 플레이 수를 나타내는)를 추가합니다.또, 각 팀의 팀 노드를 추가하고, 각 게임 노드 {i, j}를 i< j to V로 접속해, 엣지로부터 각 팀간의 플레이수를 나타내는 capacity_ij r로 접속합니다.또한 각 팀별로 팀 노드를 추가하고 각 게임 노드 {i, j}를 2개의 팀 노드 i, j와 연결하여 둘 중 하나가 승리할 수 있도록 합니다.이러한 엣지의 흐름 값을 제한할 필요가 없습니다.마지막으로, 엣지는 팀 노드 i에서 싱크 노드 t로 만들어지며, w + r_k – w의_i 용량은_k 팀 i가 w + r_k 보다_k 많이 우승하는 것을 막기 위해 설정됩니다. S는 리그에 참여하는 모든 팀의 세트이며, 다음과 같이 합니다.

( - { ) 、 {- { < r \ $display$r ( S - \ { k \ ) = \ $sum$_ {$i$ , j \ $in$\ { S - \ k \ } \ $sum$i <$j$ } $r$_ { $j$} { i

이 방법에서는 네트워크 G에 크기 r(S - {k})의 흐름 값이 존재하는 경우에만 팀 k가 제거되지 않는다고 주장됩니다.상기 기사에서는 이 흐름 값이 s에서 t까지의 최대 흐름 값임을 증명하고 있습니다.

항공사 일정

항공업계에서 가장 큰 문제는 승무원들의 스케줄 설정이다.항공사 일정 문제는 확장된 최대 네트워크 흐름의 적용으로 간주할 수 있다.이 문제의 입력은 각 비행기의 출발 및 도착 장소와 시간에 대한 정보를 포함하는 일련의 비행 F입니다.항공사 일정표 작성의 한 가지 버전에서 목표는 최대 k명의 승무원과 함께 실행 가능한 일정을 작성하는 것이다.

이 문제를 해결하기 위해서는 경계순환이라고 불리는 순환문제의 변형을 사용합니다.이것은 네트워크 흐름 문제의 일반화이며, 에지 흐름의 하한에 대한 제약이 추가되어 있습니다.

G = (V, E)를 s,t µ V를 소스와 싱크 노드로 하는 네트워크로 합니다.각 비행 i의 소스와 목적지에 대해 V에 노드_i s를 소스로서 노드_i d를 플라이트 i의 목적지 노드로서 노드 d를 추가한다.또한 E에 다음 모서리를 추가합니다.

1. 와 각 s_i 사이의 용량 [0, 1]을 가진 에지.
2. 각_i d와 t 사이에 용량 [0, 1]을 가진 가장자리.
3. s와_i d의_i 각 쌍 사이에 용량 [1, 1]을 가진 에지.
4. 소스_j s가 비행 i의 목적지로부터 합리적인 시간과 비용으로 도달할 수 있는 경우, 각_i d와_j s 사이에 용량 [0, 1]을 가진 에지.
5. s와 t 사이의 용량 [0, θ]을 가진 에지.

상기 방법에서는 s와 t 사이의 G에서 k의 흐름값을 구하는 것이 최대 k명의 ^[24]승무원과 함께 비행 세트 F에 대한 실행 가능한 일정을 찾는 것과 같다는 것을 주장하고 증명한다.

항공사 일정의 또 다른 버전은 모든 비행을 수행하기 위해 최소한 필요한 승무원을 찾는 것이다.이 문제에 대한 답을 찾기 위해, 각 비행이 세트 A와 세트 B에 복사본을 갖는 초당 그래프 = (A b B, E)가 생성됩니다.같은 평면이 비행 i 후 j를 할 수 있으면 i∈A는 jbB에 접속된다.G'의 매칭은 F에 대한 스케줄을 유도하며, 이 그래프에서 분명히 최대 초당 매칭은 최소 ^[24]승무원 수로 항공사 일정을 생성한다.이 문서의 Application 부분에서 언급되었듯이 최대 카디널리티 이분 매칭은 최대 흐름 문제의 응용 프로그램입니다.

순환 수요 문제

상품을 생산하는 공장도 있고 상품을 배달해야 하는 마을도 있다.그것들은 도로망으로 연결되어 있으며, 각 도로에는 최대 물량 c가 흐를 수 있다.문제는 수요를 충족시키는 발행부수가 있는지 찾아내는 것이다.이 문제는 최대 흐름 문제로 변환할 수 있습니다.

1. 송신원노드를 추가하고, 그 엣지를 capacity_i p를 가지는 모든 공장 노드_i f에 추가합니다.여기서_i p는_i 공장 f의 생산 레이트입니다.
2. 싱크 노드 t를 추가하고 용량_i d를 가진 모든 마을_i v에서 t에 가장자리를 추가합니다. 여기서_i d는 마을_i v의 요구 속도입니다.

G = (V, E)를 이 새로운 네트워크로 합니다.다음과 같은 경우에만 수요를 충족하는 순환이 존재합니다.

최대 흐름값(G) $=$ $di$_{i\$in$ v$}d_{i$

순환이 존재하는 경우, 최대 흐름 솔루션을 살펴보면 수요를 충족하기 위해 특정 도로로 얼마나 많은 물품을 보내야 하는지에 대한 답을 얻을 수 있습니다.

이 문제는 일부 ^[25]가장자리의 흐름에 하한을 추가하여 확장할 수 있습니다.

이미지 세그멘테이션

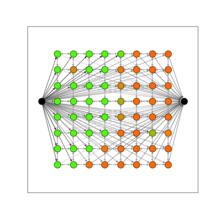
클라인버그와 타도스는 책에서 이미지를 ^[27]분할하는 알고리즘을 제시한다.그들은 이미지에서 배경과 전경을 찾는 알고리즘을 제시한다.보다 정확하게는, 비트맵을 다음과 같이 모델화한다.a_i a 0은 화소 i가 전경에 속할 가능성, b_i 0 0은 화소 i가 배경에_ij 속할 가능성, p는 인접한 2개의 화소 i, j가 전경에, 다른 화소가 배경에 배치될 경우 패널티이다.목표는 다음 수량을 최대화하는 픽셀 집합의 파티션(A, B)을 찾는 것입니다.

${\displaystyle q}$ ${\displaystyle (}$ ${\displaystyle A}$,${\displaystyle }$B ) ${\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{i}}$ i${\displaystyle {}_{}\underset{}{、}}$ ${\displaystyle A_{}}$ + i${\displaystyle \underset{}{b}}$ ${\displaystyle B_{}}$i -${\displaystyle \underset{i\begin{array}{c},\end{array}}{}}$ ${\displaystyle \underset{}{\begin{array}{c}j\end{array}}}$ ${\displaystyle \underset{}{\begin{array}{c}인접\\ \\ \end{array}}}$ A ${\displaystyle \underset{}{\begin{array}{c}\cap \end{array}}}$ {${\displaystyle \underset{}{\begin{array}{c}i\end{array}}}$ , ${\displaystyle \underset{}{\begin{array}{c}j\end{array}}}$} ${\displaystyle \underset{}{\begin{array}{c}=\end{array}}}$ ${\displaystyle \underset{}{\begin{array}{}1\end{array}}{}_{}}$ p ${\displaystyle i_{}}$ { $displaystyle$q ($A$ , B ) = \ $sum$_ {$i$ \ $in A$} $a$_ { i$$} + \ $sum$_ { i \ $in$ B $} _$ { i }

실제로 A의 픽셀(전경으로 간주)은_i a를 얻고 B의 모든 픽셀(배경으로 간주)은_i b를 얻는다.두 개의 인접한 픽셀 i와 j 사이의 경계에서 p를 느슨하게_ij 합니다.이는 수량을 최소화하는 것과 같다.

$\displaystyle q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\cap {i,j\}=1\end}p_{ij}$

왜냐면

$\displaystyle q(A,B)=\sum _{i\in A\cup B}a_{i}+\sum _{i\in A\cup B}b_{i}-q'(A,B)}$

이제 노드가 픽셀, 소스 및 싱크인 네트워크를 구축합니다(오른쪽 그림 참조).a의 무게로 소스를_i i픽셀에 연결합니다.무게_i b의 가장자리에 의해 픽셀 i를 싱크대에 연결합니다.무게_ij p로 픽셀 i를 픽셀 j에 연결합니다.이제 해당 네트워크의 최소 컷(또는 그에 상응하는 최대 플로우)을 계산해야 합니다.마지막 그림은 최소 절단을 보여줍니다.

내선번호

1. 최소 비용 흐름 문제에서 각 에지(u, v)에는 용량 외에 비용 계수_uv a도 있습니다.에지를 통과하는 흐름이 f일_uv 경우 총 비용은 af입니다_uvuv.최소 비용으로 소정의 크기 d의 플로우를 찾아야 합니다.대부분의 변형에서 비용 계수는 양수이거나 음수일 수 있습니다.이 문제에는 다양한 다항 시간 알고리즘이 있습니다.

2. 최대 흐름 문제는 분리 제약에 의해 증가할 수 있습니다.부정 분리 제약조건은 특정 에지 쌍이 동시에 0이 아닌 흐름을 가질 수 없다고 말합니다.긍정 분리 제약조건은 특정 에지 쌍에서 적어도 하나는 0이 아닌 흐름을 가져야 한다고 말합니다.네거티브한 제약 조건에서는 단순한 네트워크에서도 문제는 NP-hard가 됩니다.양의 제약조건에서는 프랙셔널플로우가 허용되면 문제는 다항식이지만 플로우가 ^[28]적분해야 하는 경우에는 NP-hard일 수 있습니다.

레퍼런스

추가 정보

• Joseph Cheriyan and Kurt Mehlhorn (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters. 69 (5): 239–242. CiteSeerX 10.1.1.42.8563. doi:10.1016/S0020-0190(99)00019-8.
• Daniel D. Sleator and Robert E. Tarjan (1983). "A data structure for dynamic trees" (PDF). Journal of Computer and System Sciences. 26 (3): 362–391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
• Eugene Lawler (2001). "4. Network Flows". Combinatorial Optimization: Networks and Matroids. Dover. pp. 109–177. ISBN 978-0-486-41453-9.