피쳐 지향 프로그래밍

Feature-oriented programming
프로그래밍 패러다임

컴퓨터 프로그래밍에서 기능 지향 프로그래밍(FOP) 또는 기능 지향 소프트웨어 개발(FOSD)은 소프트웨어 제품군(SPL)에서의 프로그램 생성과 프로그램의 점진적 개발을 위한 프로그래밍 패러다임이다.

역사

vertical stacking of layers
레이어 스택과 변환 구성 간의 연결

FOSD는 1980년대 후반 네트워크 프로토콜과 확장 가능한 데이터베이스 시스템의 계층 기반 설계와 추상화 수준에서 생겨났다.[1] 프로그램은 겹겹이 쌓여 있었다. 각 계층은 이전에 구성된 계층에 기능을 추가했고 계층의 다른 구성이 다른 프로그램을 생성했다. 놀랄 것도 없이, 그러한 디자인을 표현하기 위해서는 콤팩트한 언어가 필요했다. 초등 대수학에서는 지폐에 적합하다: 각 계층은 새로운 프로그램을 생산하기 위해 기존 프로그램에 새로운 코드를 추가하는 함수(프로그램 변환)였고, 프로그램의 디자인은 표현, 즉 변환(레이어)의 구성으로 모델링되었다. 왼쪽 그림은 층 i, j, h(h가 맨 아래에 있고 i가 맨 위에 있는 곳)의 층을 보여준다. 대수적 표기 i(j(h), i•j•h 및 i+j+h는 이러한 설계를 표현하기 위해 사용되어 왔다.

시간이 지남에 따라 계층은 형상과 동일시되었고, 여기서 형상은 프로그램 기능성의 증가다. 프로그램 설계와 생성을 위한 패러다임은 관계형 질의 최적화의 결과로 인식되었는데, 여기서 질의 평가 프로그램은 관계형 대수식으로 정의되고 질의 최적화는 표현형 최적화였다.[2] 소프트웨어 제품군은 각 프로그램이 특징의 고유한 구성으로 정의되는 프로그램의 제품군이다. FOSD는 그 이후로 형상 기반 프로그램 생성을 지원하기 위한 형상 모듈화, 도구, 분석 및 설계 기법의 연구로 발전했다.

2세대 FOSD 연구는 통신에서 유래한 특징 상호작용에 관한 것이었다. 후에 특징 중심 프로그래밍이라는 용어가 생겨났다;[3] 이 작품은 계층들 사이의 상호작용을 노출시켰다. 상호작용은 다른 형상과 합성할 때 형상을 수정해야 한다.

제3세대 연구는 모든 프로그램이 다중 표현(예: 출처, makefile, documentation 등)을 가지고 있다는 사실에 초점을 맞추었으며 프로그램에 특징을 추가하는 것은 모든 것이 일관되도록 각각의 표현을 상세히 설명해야 한다. 또한 일부 표현은 다른 표현으로부터 생성(또는 파생)될 수 있다. 아래 절에서는 가장 최근에 개발된 FOSD의 3세대, 즉 GenVoca,[1] EXM,[4] FOMDD의[5][6] 수학이 설명되며, FOSD 도구를 사용하여 개발된 제품군에 대한 링크가 제공된다. 또한 FOSD의 모든 세대에 적용되는 4가지 추가 결과는 FOSD 메타모델, FOSD 프로그램 큐브, FOSD 피쳐 인터랙션이다.

겐보카

GenVoca(제네시스와 아보카라는 이름의 포트만테아우)[1]는 제품군의 프로그램을 정의하기 위한 구성적 패러다임이다. 기본 프로그램은 값이라고 하는 0-ari 함수 또는 변환이다. 

  f -- feature f h - feature h가 있는 base program

및 기능은 프로그램을 구체화(확장, 확장, 세분화)하는 단일 기능/구성이다. 

  i + x - 프로그램 x j + x에 기능 i 추가 - 프로그램 x에 기능 j 추가

여기서 +는 함수 구성을 나타낸다. 프로그램 설계는 명명된 표현식이다. 예: 

  p1 = j + f - 프로그램 p는1 특징 j를 가지고 있고2 f = j + h - 프로그램 p는2 특징 j를 가지고 있고 h3 = i + j + h - 프로그램 p는3 특징 i, j, h를 가지고 있다.

도메인 또는 소프트웨어 제품군의 GenVoca 모델은 기본 프로그램과 기능의 모음입니다(MetaModels 및 프로그램 큐브 참조). 생성될 수 있는 프로그램(expression)은 제품 라인을 정의한다. 표현식 최적화는 프로그램 설계 최적화, 표현식 평가는 프로그램 생성이다.

참고: GenVoca는 프로그램의 단계적 개발, 즉 프로그램 이해와 자동화된 프로그램 구성의 핵심인 설계 단순성과 이해가능성을 강조하는 프로세스를 기반으로 한다. 위의 p 프로그램을3 고려하라: 기본 프로그램 h로 시작한 다음 feature j가 추가되고(읽기: feature j의 기능은 h의 codebase에 추가됨), 마지막으로 feature i가 추가된다(읽기: feature i의 기능은 j•h의 codebase에 추가됨).
참고: 모든 형상의 조합이 의미 있는 것은 아니다. 형상 모델(제안 공식으로 번역할 수 있음)은 형상의 법적 조합을 정의하는 그래픽 표현이다.[7]
참고: 보다 최근의 GenVoca 공식은 대칭적이다: 기본 프로그램 0(빈 프로그램)이 하나뿐이며, 모든 기능은 단일한 기능이다. 이는 GenVoca가 중첩에 의해 프로그램 구조를 구성한다는 해석, 즉 복잡한 구조가 단순한 구조를 중첩시켜 구성한다는 해석을 시사한다.[8][9] 그러나 GenVoca의 또 다른 개혁은 단조로움이다: GenVoca 모델은 구성 연산이 있는 특징들의 집합이다(•; 구성은 연관성이 있고 ID 요소는 1이다. 비록 모든 작곡이 가능하지만, 모두가 의미 있는 것은 아니다. 그것이 피처모델의 이유다.

GenVoca 기능은 원래 C 전처리기(C precessor)를 사용하여 구현되었다.#ifdef feature ... #endif) 기법. 믹스인 레이어라고 불리는 보다 진보된 기법은 객체 지향의 협업 기반 설계에 특징의 연결을 보여주었다.

앞으로

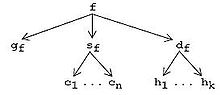
응용설계를 위한 대수적 계층적 방정식(AHEAD)[4]은 두 가지 방법으로 GenVoca를 일반화했다. 먼저 투플로서 겐보카 가치의 내부 구조를 밝혔다. 모든 프로그램에는 소스, 문서, 바이트 코드, makefile과 같은 여러 가지 표현이 있다. GenVoca 값은 프로그램 표현의 튜플이다. 예를 들어, 파서들의 제품 라인에서, 베이스 파서 f는 그것의 문법 gf, 자바 소스 s 및f 문서 d에f 의해 정의된다. 파서 f는 튜플 f=[gf, sf, d]에f 의해 모델링된다. 각 프로그램 대표자는 하위표시를 가질 수 있으며, 그들도 하위표시를 반복적으로 가질 수 있다. 일반적으로 GenVoca 값은 특정 프로그램의 표현 계층을 정의하는 중첩된 튜플의 튜플이다.

프로그램 아티팩트 간의 계층적 관계

예 터미널 표시가 파일이라고 가정해 보십시오. AWARD에서, 문법f g는 단일 BNF 파일에 대응하고, source s는f Java 파일의 tuple[c1…cn]에 대응하며, 설명서 d는f HTML 파일[h…h]의1 tuple이다k. GenVoca 값(내포 튜플)은 지시된 그래프로 나타낼 수 있다. 파서 f에 대한 그래프는 오른쪽 그림에 표시된다. 화살표는 투영, 즉 튜플에서 그것의 구성 요소 중 하나로의 매핑을 나타낸다. EXIT는 튜플을 파일 디렉토리로 구현하기 때문에 f는 파일f g와 하위 디렉토리의f s와f d를 포함하는 디렉토리다. 마찬가지로 디렉토리 s에는f c1…cn 파일이 들어 있고, 디렉토리 df에는 h1…hk 파일이 들어 있다.

참고: 파일은 계층적으로 더 분해될 수 있다. 각 Java 클래스는 멤버와 다른 클래스 선언(예: 초기화 블록 등)으로 분해될 수 있다. 여기서 중요한 아이디어는 EXIT의 수학이 재귀적이라는 것이다.

둘째, FORD는 델타라고 불리는 단항 함수의 내포된 튜플로서 형상을 표현한다. 델타(Deltas)는 프로그램 개선(반전-보존 변환), 확장(반전-확장 변환) 또는 상호작용(반전-변환 변환)이 될 수 있다. 우리는 중립적인 용어 "델타"를 사용하여 FOSD에서 각각 발생하듯이 이러한 모든 가능성을 나타낸다.

예를 들어 피쳐 j가 문법을 g(j 규칙과 토큰이 추가됨)로 하고 소스 코드를 {\ \Delta j(새로운 클래스 및 멤버가 추가되고 기존 메서드가 수정됨)로 확장하고, 문서를 {\j. 형상 j에 대한 델타(delta)의 튜플은 j=[ j, {\j, style j]에 의해 모델링되며, 우리는 이를 델타 튜플이라고 부른다. 델타 튜플의 원소는 그 자체로 델타 튜플이 될 수 있다. 예: 는j 형상 j에 의해 각f 클래스에 수행되는 변경 사항을 나타낸다. 즉, Δ }j=[ {\} 1… n]]. 프로그램의 표현은 내포 벡터 추가에 의해 재귀적으로 계산된다. 파서 p2(GenVoca 식이 j+f인 경우)에 대한 표현은 다음과 같다. 

  P2)j+f--GenVoca 표현)[Δ{\displaystyle \Delta}gj,Δ{\displaystyle \Delta}sj,Δ{\displaystyle \Delta}dj]+[gf, sf, df]--대체)[Δ{\displaystyle \Delta}gj+gf,Δ{\displaystyle \Delta}sj+sf,Δ{\displaystyle \Delta}dj+df].         검토 해 보았고 요소별 튜플

즉, p의2 문법은 그 확장자로 구성된 기본 문법( } j+gf), p의 출처는2 그 확장자로 구성된 기본 소스( }jf 등이다. 델타 튜플의 요소 자체가 델타 튜플이 될 수 있기 때문에 구성 재귀: Δ {\\Delta }jf= [ }n … c]+[c1n …=[ 1+c1…… n+cn]. 요약하면 GenVoca 값은 프로그램 아티팩트의 내포된 튜플이며, 형상은 내포된 델타 튜플이며, 여기서 + 벡터 추가에 의해 그것들을 재귀적으로 구성한다. 이것이 바로 전방의 본질이다.

위에서 제시된 아이디어는 두 가지 FOSD 원칙을 구체적으로 드러낸다. 균일성의 원칙은 모든 프로그램 유물을 동일한 방식으로 처리하고 수정한다고 명시하고 있다. (이것은 위의 다른 유물의 유형에 대한 델타(deltas)로 증명된다.) 확장성 원리는 모든 수준의 추상화를 균일하게 취급한다고 명시한다. (이것은 위의 튜플의 계층적 보금자리를 발생시킨다.)

AWARD의 원래 구현은 동일성과 확장성의 원리를 모두 보여주는 WIRD Tool Suite와 Jak 언어다. 차세대 도구(CIDE 및 기능 포함)집이다.[11]

FOMDD

프로그램 아티팩트 간의 파생 및 정교함 관계

FOMDD([5][6]Feature-Drivened Model-Driven Design)는 OWN의 아이디어를 MDD(Model-Driven Design)(예: K.A)와 결합한다. MDA(모델 기반 아키텍처). FREAD 기능은 프로그램에 기능이 추가될 때 프로그램 아티팩트의 잠금 단계 업데이트를 캡처한다. 그러나 파생어를 표현하는 프로그램 공예품들 사이에는 다른 기능적 관계가 있다. 예를 들어, 문법 g와f 그 파서 소스 s 사이의f 관계는 컴파일러 컴파일러 도구(예: 자바크)에 의해 정의된다. 마찬가지로, 자바 소스f s와 그것의 바이트 코드 bf 사이의 관계는 자바 컴파일러에 의해 정의된다. 통근 도표는 이러한 관계를 표현한다. 개체는 프로그램 표현이고, 아래쪽 화살표는 파생형이며, 수평 화살표는 델타형이다. 오른쪽 그림은 p3 = i+j+h = [g3,s3,b3] 프로그램의 통근 도표를 보여준다.

통근 도표의 기본 속성은 두 물체 사이의 모든 경로가 동등하다는 것이다. 예를 들어 파서 h(왼쪽 위 객체)의 문법 g에서h 파서 p(그림3 오른쪽 아래3 객체)의 바이트코드 b를 도출하여 b로3 정제하는 한 가지 방법인 반면h, g를h g로3 정제하는 다른 방법은 delta composition을 나타내고 ()는3 함수 또는 도구 응용이다. 

  b3 = j + \i + javac(javac(gh ) = javac(Javac(  style  }gajh = javac(javac)(javac( \deplaystyc)( Δ {\daystypec)( \data \data)( \Delta \ \Delta \Delta \data \

파서 h의 문법 g에서h 파서 p의3 바이트코드 b를3 도출할 수 있는 ( ) 개의 가능한 경로가 있다. 각 경로는 실행이 시작 개체(gf)에서 대상 개체(b3)를 생성하는 메타프로그램을 나타낸다. 잠재적인 최적화가 있다: 통근 다이어그램의 각 화살표를 가로지르는 데는 비용이 든다. 통근 도표에서 두 물체 사이의 가장 저렴한(즉, 최단) 경로는 지오데식(geodesic)으로, 주어진 물체로부터 목표 물체를 생산하는 가장 효율적인 메타프로그램이다.

참고: "비용 메트릭"은 통화 가치가 될 필요는 없으며, 원가는 생산 시간, 피크 또는 총 메모리 요구 사항, 전력 소비량 또는 "해설의 ease"와 같은 비공식 메트릭스 또는 위의 조합(예: 다목적 최적화)으로 측정할 수 있다. 지오데틱의 생각은 일반적이며, 이 보다 일반적인 맥락에서 이해되고 인식되어야 한다.
참고: 지오데틱에 m 시작 객체와 n 끝 객체가 있을 수 있다; m=1과 n>1일 때 이것은 방향 슈타이너 트리 문제(NP-hard)이다.

통근 도표는 최소한 두 가지 이유로 중요하다. (1) 공예품의 생성 최적화 가능성이 있다(예: 지오데틱스). (2) 출발 물체로부터 대상 물체를 구성하는 다른 방법을 명시한다.[5][12] 도표를 통과하는 경로는 툴 체인에 해당된다. FOMDD 모델이 일관성을 유지하려면 한 물체를 다른 물체에 매핑하는 모든 툴 체인이 실제로 동등한 결과를 산출한다는 것을 입증(또는 시험을 통해 입증)해야 한다. 그렇지 않으면 하나 이상의 도구에 버그가 있거나 FOMDD 모델이 잘못되었다.

참고: 위의 아이디어들은 범주 이론에 의해 영감을 받았다.[5][6]

적용들

참고 항목

참조

  1. ^ a b c "Design and Implementation of Hierarchical Software Systems with Reusable Components" (PDF).
  2. ^ "Access Path Selection In Relational Databases".
  3. ^ "Feature-Oriented Programming: A Fresh Look at Objects". Archived from the original on 2003-08-03. Retrieved 2015-12-16.
  4. ^ a b "Scaling Step-Wise Refinement" (PDF).
  5. ^ a b c d "Feature Oriented Model Driven Development: A Case Study for Portlets" (PDF).
  6. ^ a b c Trujillo, Salvador; Azanza, Maider; Díaz, Óscar (October 2007). "Generative Metaprogramming". GPCE '07: Proceedings of the 6th international conference on Generative programming and component engineering: 105–114. doi:10.1145/1289971.1289990.
  7. ^ "Feature Models, Grammars, and Propositional Formulas" (PDF).
  8. ^ "An Algebra for Features and Feature Composition" (PDF).
  9. ^ "Superimposition: A Language-Independent Approach to Software Composition" (PDF).
  10. ^ "Guaranteeing Syntactic Correctness for all Product Line Variants: A Language-Independent Approach" (PDF).
  11. ^ "FeatureHouse: Language-Independent, Automated Software Composition" (PDF).
  12. ^ "Testing Software Product Lines Using Incremental Test Generation" (PDF).