단치히-울프 분해
Dantzig–단치히-울프 분해는 특수 구조로 선형 프로그래밍 문제를 해결하는 알고리즘이다.원래는 조지 단치히와 필립 울프가 개발했으며, 1960년에 처음 출판되었다.[1]선형 프로그래밍에 관한 많은 텍스트에는 이 분해 알고리즘을 논하는 전용 섹션이 있다.[2][3][4][5][6][7]
단치히-울프 분해는 대규모 선형 프로그램의 트랙터성을 개선하기 위해 지연된 기둥 생성에 의존한다.개정된 심플렉스 알고리즘을 통해 해결되는 대부분의 선형 프로그램의 경우, 각 단계에서 대부분의 컬럼(변수)이 기초가 되지 않는다.그러한 체계에서 최소한 현재 활성 열(근거)을 포함하는 마스터 문제는 하위 문제 또는 하위 문제를 사용하여 해당 열을 포함시켜 객관적 기능을 향상시키는 기초 진입을 위한 열을 생성한다.
필수양식
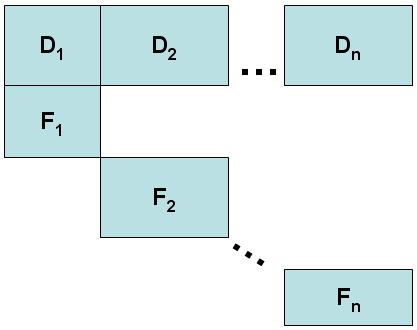
단치히-을 사용하기 위해서는울프 분해, 선형 프로그램의 구속조건 행렬은 특정한 형태를 가져야 한다.제약조건 집합은 "연결", "커플링" 또는 "만족" 제약조건으로 식별되어야 하며, 제약조건에 포함된 많은 변수에서 0이 아닌 계수가 있다.변수가 한 하위트리거 내에 0이 아닌 계수를 가질 경우 다른 하위트리거에서 0이 아닌 계수를 가질 수 없도록 나머지 제약조건은 독립 하위트리거로 분류할 필요가 있다.이 설명은 다음과 같이 시각화된다.
D 행렬은 연결 제한조건을 나타내며 각 F는i 독립적인 하위 행렬을 나타낸다.F 서브매트릭스가 하나만 있을 때 알고리즘을 실행할 수 있다는 점에 유의한다.
문제개혁
필요한 양식을 파악한 후 원래의 문제를 마스터 프로그램과 n개의 하위 프로그램으로 개편한다.이 개혁은 비어 있지 않고 경계가 있는 볼록한 다면체의 모든 점이 그것의 극점의 볼록한 조합으로 표현될 수 있다는 사실에 의존한다.
새로운 마스터 프로그램의 각 열은 하위 문제 중 하나에 대한 해결책을 나타낸다.마스터 프로그램은 현재 사용할 수 있는 하위 문제 해결책 세트를 고려할 때 연결 장치 제약 조건을 충족하도록 강제한다.그런 다음 마스터 프로그램은 원래의 선형 프로그램에 대한 전체적인 목표가 개선되도록 하위 문제에 추가적인 해결책을 요청한다.
알고리즘
이행과 관련하여 여러 가지 변화가 있지만 단치히-Wolfe 분해 알고리즘은 다음과 같이 간단히 설명할 수 있다.
- 축소된 마스터 프로그램에 대한 실현 가능한 해결책부터 시작하여 하위 문제가 마스터 프로그램의 현재 목표를 개선하는 해결책을 제공할 수 있도록 각 하위 문제에 대한 새로운 목표 기능을 공식화한다.
- 하위 문제는 새로운 목표 기능을 고려하여 다시 해결된다.각 하위 문제에 대한 최적의 값이 마스터 프로그램에 제공된다.
- 마스터 프로그램은 원래 문제의 목적을 개선하기 위한 각 열의 능력에 기초하여 하위 문제에 대한 해결책에 의해 생성된 새로운 열의 하나 또는 전부를 통합한다.
- 마스터 프로그램은 단순x 알고리즘의 x 반복을 수행하며, 여기서 x는 통합된 열의 수입니다.
- 목표가 개선되면 1단계로 이동하십시오.그렇지 않으면 계속하십시오.
- 하위 문제에서 나오는 어떤 새로운 컬럼으로도 마스터 프로그램을 더 이상 개선할 수 없으므로 반환된다.
실행
단치히 이행 사례도 있다.AMP[8] 및 GAMS[9] 수학 모델링 언어로 제공되는 Wolfe 분해.오픈 소스 GNU 선형 프로그래밍 키트를 활용하는 일반적인 병렬 구현이 있다[10].
알고리즘은 하위 문제의 해결책이 완전히 독립적이기 때문에 병렬로 해결되도록 구현될 수 있다.이러한 경우, 마스터 프로그램에 대한 옵션으로 열을 마스터에 통합하는 방법이 있다.마스터는 각 하위 문제가 완료될 때까지 기다렸다가 목표를 개선하는 모든 열을 통합하거나 해당 열의 더 작은 부분 집합을 선택할 수 있다.또 다른 옵션은 마스터가 사용 가능한 첫 번째 열만 선택한 다음 최신 열의 통합에 기초하여 새로운 목표를 가진 모든 하위 문제를 중지하고 재시작할 수 있다는 것이다.
구현을 위한 또 다른 설계 선택은 알고리즘의 각 반복에서 기초를 벗어나는 열을 포함한다.이러한 열은 향후 반복 후에 일부 정책을 통해 유지, 즉시 폐기 또는 폐기될 수 있다(예를 들어, 10번 반복할 때마다 모든 비기본 열을 제거).
단치히-울프 일반 및 단치히-울프 병렬 연산에 대한 A(2001) 연산 평가는 J. R의 박사 논문이다.테봇[11]
참고 항목
참조
- ^ George B. Dantzig; Philip Wolfe (1960). "Decomposition Principle for Linear Programs". Operations Research. 8: 101–111. doi:10.1287/opre.8.1.101.
- ^ Dimitris Bertsimas; John N. Tsitsiklis (1997). Linear Optimization. Athena Scientific.
- ^ George B. Dantzig; Mukund N. Thapa (1997). Linear Programming 2: Theory and Extensions. Springer.
- ^ Vašek Chvátal (1983). Linear Programming. Macmillan.
- ^ Maros, István; Mitra, Gautam (1996). "Simplex algorithms". In J. E. Beasley (ed.). Advances in linear and integer programming. Oxford Science. pp. 1–46. MR 1438309.
- ^ Maros, István (2003). Computational techniques of the simplex method. International Series in Operations Research & Management Science. Vol. 61. Boston, MA: Kluwer Academic Publishers. pp. xx+325. ISBN 1-4020-7332-1. MR 1960274.
- ^ Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan ed.). Mineola, New York: Dover Publications, Inc. pp. xiii+523. MR 1888251.
- ^ "AMPL code repository with Dantzig–Wolfe example". Retrieved December 26, 2008.
- ^ Kalvelagen, Erwin (May 2003), Dantzig-Wolfe Decomposition with GAMS (PDF), retrieved 2014-03-31.
- ^ "Open source Dantzig-Wolfe implementation". Retrieved October 15, 2010.
- ^ Tebboth, James Richard (2001). A computational study of Dantzig-Wolfe decomposition (PDF) (PhD thesis). University of Buckingham, United Kingdom.