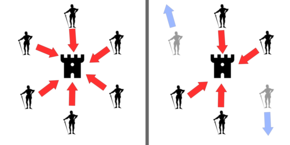
비잔틴 단층
Byzantine fault비잔틴 오류(또한 비잔틴 일반 문제, 인터랙티브 일관성, 소스 일치, 오류 눈사태, 비잔틴 합의 문제 및 비잔틴[1] 실패)는 컴퓨터 시스템, 특히 분산 컴퓨팅 시스템의 상태이며, 구성요소가 고장 났는지 여부에 대한 불완전한 정보가 있습니다.이 용어는 "잔틴 장군 문제"[2]라는 우화에서 유래한 것으로, 시스템의 치명적인 실패를 피하기 위해, 시스템의 행위자들이 일치된 전략에 동의해야 하지만, 이러한 행위자들 중 일부는 신뢰할 수 없는 상황을 묘사하기 위해 개발되었습니다.
비잔틴의 장애에서는 서버 등의 컴포넌트가 장애 검출 시스템에 일관성이 없고 기능하고 있는 것처럼 보여 관찰자마다 다른 증상을 나타낼 수 있습니다.다른 컴포넌트가 장애를 선언하고 네트워크로부터 셧다운하는 것은 어렵습니다.이는 우선 어떤 컴포넌트에 장애가 발생했는지에 대한 합의에 도달해야 하기 때문입니다.비잔틴 폴트 톨러런스(BFT)는 이러한 조건에 대한 폴트 톨러런스 컴퓨터 시스템의 복원력입니다.
유추
가장 간단한 형태로는, 많은 장군들이 요새를 공격하고 있고, 공격할지 후퇴할지는 단체로 결정해야만 한다.어떤 장군들은 공격을 선호하고 다른 장군들은 후퇴를 선호할 수도 있다.중요한 것은 모든 장군들이 공통된 결정에 동의한다는 것이다. 왜냐하면 소수의 장군들이 성의 없이 공격하는 것은 패배가 되고, 협공 공격이나 협공 후퇴보다 더 나빠질 것이기 때문이다.
차선의 전략에 투표할 수도 있고 선별적으로 투표할 수도 있는 배신적인 장군들의 존재로 인해 문제가 복잡해졌다.예를 들어 9명의 장성이 찬성표를 던지고 그 중 4명이 공격을 지지하고 4명이 후퇴를 찬성하면 제9대 장성은 후퇴표를 던지고 나머지 장성은 공격표를 던질 수 있다.제9대 장군으로부터 퇴각표를 받은 자는 퇴각하고 나머지는 공격한다(공격자들에게는 잘 되지 않을 수 있음).문제는 장군들이 물리적으로 떨어져 있고 표를 전달하지 못하거나 거짓 표를 위조할 수 있는 메신저를 통해 표를 보내야 하기 때문에 더 복잡하다.
결의안
충성스러운(무과실) 장군들이 전략에 대해 과반수의 동의를 얻으면 비잔틴의 폴트 톨러런스를 달성할 수 있습니다.누락된 메시지에 기본 투표 값이 지정될 수 있습니다.예를 들어 누락된 메시지는 "null" 값을 지정할 수 있습니다.또한 무효표가 과반수인 경우 사전 할당된 디폴트 전략을 사용할 수 있다(예: 후퇴).[3]
컴퓨터 시스템에 대한 이 이야기의 전형적인 매핑은 컴퓨터가 일반이고 디지털 통신 시스템 링크가 메신저라는 것이다.이 문제는 의사결정 및 보안 문제로 비유되지만 전자제품에서는 잘못된 전압 등의 장애가 암호화 프로세스를 통해 전파될 수 있기 때문에 암호화 디지털 서명만으로는 해결할 수 없습니다.따라서 컴포넌트가 한 컴포넌트에는 기능하고 다른 컴포넌트에는 결함이 있는 것처럼 보일 수 있으므로 컴포넌트의 결함 여부에 대한 공감대를 형성할 수 없습니다.
특성.
비잔틴 단층은 관찰자마다 [4]다른 증상을 보이는 단층입니다.비잔틴 장애는 [5]합의가 필요한 시스템에서 비잔틴 장애로 인해 시스템 서비스가 손실되는 것입니다.
비잔틴의 폴트 톨러런스의 목적은 시스템의 다른 컴포넌트가 서로 합의에 이르지 못하도록 하는 증상의 유무에 관계없이 시스템컴포넌트의 장애를 방어하는 것입니다.시스템이 올바르게 동작하기 위해서는 이러한 합의가 필요합니다.
비잔틴 폴트 톨러런스 시스템의 나머지 동작상 올바른 컴포넌트는 서비스를 유지하기에 충분한 수의 컴포넌트가 있는 경우 원래 의도한 대로 시스템의 서비스를 계속 제공할 수 있습니다.
비잔틴 고장은 고장 모드 중 가장 일반적이고 가장 어려운 종류의 고장으로 간주됩니다.이른바 페일 스톱 장애 모드는 스펙트럼의 가장 단순한 끝을 차지합니다.Fail-stop 장애 모드는 단순히 장애 발생의 유일한 방법이 다른 노드에서 검출된 노드 크래시임을 의미하지만, 비잔틴 장애는 제약이 없음을 의미하며, 이는 장애가 발생한 노드가 기능하는 노드와 같은 데이터를 포함하는 임의의 데이터를 생성할 수 있음을 의미합니다.따라서 비잔틴의 장애는 장애 감지 시스템을 혼란스럽게 할 수 있으며, 이로 인해 내결함성이 어려워집니다.비유를 들어도 비잔틴의 실패가 반드시 적대적인 인간의 간섭을 수반하는 보안 문제는 아닙니다. 이는 순전히 전기 또는 소프트웨어 결함에서 발생할 수 있습니다.
장애와 장애라는 용어는 IEEE Computer Society's Technical Committee on Relectable Computing and Fault Tolerance와 IFIP Working Group 10.4 on Relectible Computing and [7]Fault Tolerance에 의해 구성된 "기본 개념과 용어" 공동 위원회가 처음 작성한 표준 정의에[6] 따라 사용됩니다.「신뢰성」도 참조해 주세요.
경고
비잔틴의 폴트 톨러런스는 브로드캐스트의 일관성에만 관계합니다.즉, 한 컴포넌트가 다른 컴포넌트에 동일한 값을 브로드캐스트할 때(즉, 다른 컴포넌트에 동일한 값을 송신할 때), 이들 컴포넌트는 모두 정확히 동일한 값을 수신하거나 브로드캐스트가 일관성이 없는 경우 다른 컴포넌트가 수신하는 속성입니다.공통값으로 합니다.이러한 종류의 폴트 톨러런스에는 값 자체의 정확성이 포함되지 않습니다.예를 들어 의도적으로 잘못된 값을 전송하지만 모든 컴포넌트에 일관되게 동일한 값을 전송하는 적대적 컴포넌트는 비잔틴의 폴트 톨러런스 체계에 포함되지 않습니다.
형식적 정의
설정:[8] n개의 컴포넌트로 이루어진 시스템이 있고, 그 중 t는 부정직하며, 모든 컴포넌트 간의 포인트 투 포인트 채널만을 상정하고 있습니다.
컴포넌트 A가 값 x를 브로드캐스트하려고 할 때마다 다른 컴포넌트는 서로 토론하고 A의 브로드캐스트의 일관성을 검증하여 최종적으로 공통값 y에 도달합니다.
속성:컴포넌트 A가 값 x를 브로드캐스트할 수 있는 경우 시스템은 비잔틴 장애에 저항하는 것으로 알려져 있습니다.
- A가 정직하다면 모든 정직한 구성요소는 x 값에 일치합니다.
- 어떤 경우에도 모든 정직한 구성요소는 동일한 값 y에 대해 일치합니다.
종류:이 문제는 동기 통신과 비동기 통신 모두에서 연구되고 있습니다.
위의 통신 그래프는 완전한 그래프(즉, 각 구성요소가 서로 논의할 수 있음)로 가정되지만, 통신 그래프는 제한될 수 있습니다.
또, 결함이 있는 컴퍼넌트가 서로 결탁해, 다른 컴퍼넌트를 에러로 유인하지 않는, 보다 현실적인 문제에서도 완화될 수 있습니다.이 상황에서 실용적인 알고리즘이 고안되었습니다.
역사
비잔틴의 합의를 얻는 문제는 로버트 쇼스탁에 의해 구상되고 공식화되었는데, 그는 그것을 쌍방향 일관성 문제라고 불렀다.이 작업은 1978년에 SRI International의 컴퓨터 과학 연구소에서 NASA가 후원하는[9] SIFT 프로젝트의 맥락에서 수행되었습니다.SIFT(소프트웨어 실장 폴트 톨러런스용)는 John Wensley의 두뇌의 아이로, 일부 컴퓨터에 결함이 있더라도 합의에 도달하기 위해 쌍으로 메시지를 주고받는 여러 범용 컴퓨터를 사용하는 아이디어에 기초하고 있습니다.
프로젝트 초기에는 결함이 있는 컴퓨터 n대의 음모가 올바르게 동작하고 있는 컴퓨터의 합의에 이르기 위한 노력을 "저하시킬 수" 없다는 것을 보증하기 위해 총 몇 대의 컴퓨터가 필요한지 명확하지 않았습니다.Shostak은 최소 3n+1이 필요하다는 것을 보여주었고, n=1에 사용할 수 있는 2라운드 3n+1 메시징 프로토콜을 고안했다.그의 동료인 Marshall Pease는 n > 0에 대한 알고리즘을 일반화하여 3n+1이 필요하고 충분함을 증명했습니다.이러한 결과는 Leslie Lamport의 디지털 서명을 사용한 3n의 충분성에 대한 나중에 나온 증거와 함께 "결함 [10]존재에 대한 합의 도달"이라는 학술지에 발표되었습니다.저자들은 이 논문으로 2005년 에즈거 W. 다이크스트라 상을 받았다.
대화 방식의 일관성 문제를 이해하기 쉽게 하기 위해, 람포트는 군 장성들이 도시를 공격할 계획을 세우는 화려한 우화를 고안했다.원작에서는 장군들을 알바니아군의 지휘관으로 캐스팅했다.이름은 "비잔틴"으로 바뀌었고,[11] 잭 골드버그의 제안으로 미래에 일어날 수 있는 범죄를 막기 위해 바뀌었다.이러한 문제의 공식화는 몇 가지 추가 결과와 함께 동일한 저자에 의해 1982년 논문 "비잔틴 장군 문제"[3]에서 제시되었다.
예
발생한 비잔틴 실패의 몇 가지 예는 두 개의 동등한 저널 [4][5]논문에 제시되어 있다.이러한 예와 기타 예는 NASA DASHlink 웹 [12]페이지에 설명되어 있습니다.
비잔틴 오류는 최소한 2005년까지(이 문제가 공개적으로 [13]보고되었을 때) 새로 건조된 버지니아급 잠수함에 대한 내구성 테스트 동안 불규칙한 지점에서 자주 관찰되었다.
실장
사용되고 있는 BFT의 한 예는 피어 투 피어 디지털 현금 [14]시스템인 Bitcoin이다.Bitcoin 네트워크는 병렬로 작동하여 작업 증명서가 있는 블록체인을 생성함으로써 시스템이 비잔틴의 실패를 극복하고 시스템 상태에 대한 일관성 있는 글로벌 뷰에 도달할 수 있습니다.
보잉 777 항공기 정보 관리 시스템(ARINC 659 SAFEbus 네트워크를 통해), 보잉 777 비행 제어 시스템 및 보잉 787 비행 제어 시스템과 같은 일부 항공기 시스템은 비잔틴 내결함성을 사용합니다. 이러한 시스템들은 실시간 시스템이기 때문에 이들의 비잔틴 내결함성 솔루션은 대기 시간이 매우 낮아야 합니다.예를 들어 SAFEbus는 지연 시간을 [15][16][17]1마이크로초 단위로 추가할 수 있습니다.SpaceX Dragon은 [18]설계에서 비잔틴의 내결함성을 고려합니다.
비잔틴의 Fault Tolerance 메커니즘은 수신 메시지의 다른 수신자에게 수신 메시지(또는 서명만)를 반복하는 컴포넌트를 사용합니다.이 모든 메커니즘은 메시지를 반복하는 행위가 비잔틴 증상의 전파를 차단한다고 가정합니다.안전 또는 보안 중요도가 높은 시스템의 경우, 이러한 가정이 허용 가능한 수준의 결함 범위에 부합함을 입증해야 합니다.테스트를 통해 증명을 제공할 때, 한 가지 어려움은 비잔틴 [19]증상을 가진 충분히 광범위한 신호를 생성하는 것입니다.이러한 테스트에는 전문 고장 [20][21]인젝터가 필요할 수 있습니다.
솔루션
1982년에 [3]Lamport, Shostak 및 Pease에 의해 몇 가지 초기 솔루션이 설명되었습니다.이들은 우선 장군 문제는 충성스러운 부관들이 모두 함께 행동해야 하는 '사령관과 중위' 문제를 해결하는 것으로 축소될 수 있으며, 사령관이 충성할 경우 그들의 행동은 사령관이 명령한 것과 일치해야 한다고 지적했다.
- 한 가지 해결책은 메시지가 위조될 수도 있지만, 충성스럽지 않은 장군 수가 장군들의 3분의 1 미만이면 비잔틴의 잘못을 용인할 수 있는 시나리오를 고려한다.3분의 1 이상의 반역자를 상대하는 것이 불가능하다는 것은 결국 한 명의 지휘관과 두 명의 부관 문제를 해결할 수 없다는 것을 증명하는 것이다.이를 확인하기 위해 배신자 A 중령과 B 중령 2명, C 중령 2명이 있다고 가정합니다.A가 B에게 공격하고 C에게 후퇴하도록 지시하고 B와 C가 서로 메시지를 전송하면 B와 C 중 어느 쪽도 A가 아니기 때문에 A에서 누가 배신자인지 알 수 없습니다.다른 쪽 중위는 A에서 메시지를 위조했을 가능성이 있습니다.n이 총 일반의 수, t가 그 n의 배신자의 수인 경우, n > 3 t 및 통신이 동기(경계 지연)[22]일 때만 문제에 대한 해결책이 있음을 알 수 있습니다.
- 두 번째 솔루션에는 용서할 수 없는 메시지 서명이 필요합니다.보안에 중요한 시스템의 경우 디지털 서명(현대 컴퓨터 시스템에서는 공개 키 암호화를 사용하여 실제로 실현될 수 있음)은 임의의 수의 배신자가 존재하는 경우 비잔틴의 폴트 톨러런스를 제공할 수 있습니다.그러나 안전에 중요한 시스템('보안'은 지능형 위협에 대처하는 반면 '안전'은 활동 또는 임무의 본질적인 위험에 대처하는 경우)의 경우 CRC와 같은 단순한 오류 감지 코드는 훨씬 낮은 비용으로 더 약하지만 충분한 커버리지를 제공하는 경우가 많다.이는 비잔틴 단층 및 비스잔틴 단층 모두에 해당됩니다.게다가, 때때로 보안 대책은 안전을 약화시키고 그 반대도 마찬가지입니다.따라서 암호화 디지털 서명 방식은 [23]특정 보안 위협도 없는 한 안전에 중요한 시스템에 적합한 선택사항이 아닙니다.CRC 등의 에러 검출 코드는 암호화 기술보다 우수하지만, 안전이 중요한 시스템의 액티브한 전자 기기에 대한 적절한 커버리지도 제공하지 않습니다.이는 단일 비잔틴 결함 비트를 가진 CRC 보호 메시지가 서로 다른 관찰자에게 다른 데이터를 제공하고 각 관찰자가 유효한 [4][5]CRC를 확인하는 슈뢰딩거 CRC 시나리오에 의해 설명됩니다.
- 또한 모든 장군들이 서로 직접 통신할 수 없는 일부 상황에서 비잔틴의 폴트 톨러런스 동작을 허용하는 첫 번째 두 가지 솔루션에 대한 변형도 제시된다.
비잔틴의 내결함성을 구현한 여러 시스템 아키텍처가 1980년 경에 설계되었습니다.여기에는 Draper's FTMP,[24] Honeywell's MMFCS,[25] SRI's [9]SIFT 등이 포함됩니다.
고도의 솔루션
1999년에 Miguel Castro와 Barbara Liskov는 고성능의 비잔틴 스테이트 머신 리플리케이션을 제공하는 「PBFT(Practical Virganetic Fault Tolerance)」[26]알고리즘을 도입했습니다.이 알고리즘은 초당 수천 건의 요구를 처리하여 지연 시간을 밀리초 미만으로 늘렸습니다.
PBFT 이후, 견고성과 성능을 개선하기 위해 여러 BFT 프로토콜이 도입되었습니다.예를 들어 Q/U,[27] [28]HQ, Zyzzva [29]및 ABsTracts는 [30]성능 및 비용 문제를 해결한 반면, Advark[31] 및 RBFT와 [32]같은 다른 프로토콜은 안정성 문제를 해결했습니다.또한 Adapt는[33] 적응형 방식으로 전환하여 기존 BFT 프로토콜을 활용하여 기본 조건이 변경됨에 따라 시스템의 견고성과 성능을 향상시키려 했습니다.또한 A2M-PBFT-EA[34] 및 MinBFT와 [35]같은 신뢰할 수 있는 구성요소를 활용하여 복제본 수를 줄이는 BFT 프로토콜이 도입되었습니다.
PBFT를 모티브로 한 Tendermint BFT는[36] 부분 비동기 네트워크에 도입되어 주로 Proof of Stake 블록체인에 사용됩니다.
비잔틴 장애 허용이 이상적인 속성이지만 최소 4개의 독립 관리 도메인이 필요합니다.이 제한을 완화하기 위해 스칼라 DL이 도입되어 트랜잭션 데이터베이스 시스템에서 관리 도메인이 2개뿐인 비잔틴 장애를 검출하는 "실용적인 비잔틴 장애 검출"[37] 알고리즘을 실현했습니다.
「 」를 참조해 주세요.
레퍼런스
- ^ Kirrmann, Hubert (n.d.). "Fault Tolerant Computing in Industrial Automation" (PDF). Switzerland: ABB Research Center. p. 94. Archived from the original (PDF) on 2014-03-26. Retrieved 2015-03-02.
- ^ Lamport, L.; Shostak, R.; Pease, M. (1982). "The Byzantine Generals Problem" (PDF). ACM Transactions on Programming Languages and Systems. 4 (3): 382–401. CiteSeerX 10.1.1.64.2312. doi:10.1145/357172.357176. Archived (PDF) from the original on 13 June 2018.
- ^ a b c Lamport, L.; Shostak, R.; Pease, M. (1982). "The Byzantine Generals Problem" (PDF). ACM Transactions on Programming Languages and Systems. 4 (3): 387–389. CiteSeerX 10.1.1.64.2312. doi:10.1145/357172.357176. Archived from the original (PDF) on 7 February 2017.
- ^ a b c Driscoll, K.; Hall, B.; Paulitsch, M.; Zumsteg, P.; Sivencrona, H. (2004). "The Real Byzantine Generals". The 23rd Digital Avionics Systems Conference (IEEE Cat. No.04CH37576). pp. 6.D.4–61–11. doi:10.1109/DASC.2004.1390734. ISBN 978-0-7803-8539-9. S2CID 15549497.
- ^ a b c Driscoll, Kevin; Hall, Brendan; Sivencrona, Håkan; Zumsteg, Phil (2003). "Byzantine Fault Tolerance, from Theory to Reality". Computer Safety, Reliability, and Security. Lecture Notes in Computer Science. Vol. 2788. pp. 235–248. doi:10.1007/978-3-540-39878-3_19. ISBN 978-3-540-20126-7. ISSN 0302-9743. S2CID 12690337.
- ^ Avizienis, A.; Laprie, J.-C.; Randell, Brian; Landwehr, C. (2004). "Basic concepts and taxonomy of dependable and secure computing". IEEE Transactions on Dependable and Secure Computing. 1 (1): 11–33. doi:10.1109/TDSC.2004.2. hdl:1903/6459. ISSN 1545-5971. S2CID 215753451.
- ^ "Dependable Computing and Fault Tolerance". Archived from the original on 2015-04-02. Retrieved 2015-03-02.
- ^ Matthias Fitzi (2002). "Generalized Communication and Security Models in Byzantine Agreement" (PDF). ETH Zurich.
- ^ a b "SIFT: design and analysis of a fault-tolerant computer for aircraft control". Microelectronics Reliability. 19 (3): 190. 1979. doi:10.1016/0026-2714(79)90211-7. ISSN 0026-2714.
- ^ Pease, Marshall; Shostak, Robert; Lamport, Leslie (April 1980). "Reaching Agreement in the Presence of Faults". Journal of the Association for Computing Machinery. 27 (2): 228–234. CiteSeerX 10.1.1.68.4044. doi:10.1145/322186.322188. S2CID 6429068.
- ^ Lamport, Leslie (2016-12-19). "The Byzantine Generals Problem". ACM Transactions on Programming Languages and Systems. SRI International. Retrieved 18 March 2019.
- ^ Driscoll, Kevin (2012-12-11). "Real System Failures". DASHlink. NASA. Archived from the original on 2015-04-02. Retrieved 2015-03-02.
- ^ Walter, C.; Ellis, P.; LaValley, B. (2005). "The Reliable Platform Service: A Property-Based Fault Tolerant Service Architecture". Ninth IEEE International Symposium on High-Assurance Systems Engineering (HASE'05). pp. 34–43. doi:10.1109/HASE.2005.23. ISBN 978-0-7695-2377-4. S2CID 21468069.
- ^ "Bitcoin - Open source P2P money". bitcoin.org. Retrieved 2019-08-18.
- ^ M., Paulitsch; Driscoll, K. (9 January 2015). "Chapter 48:SAFEbus". In Zurawski, Richard (ed.). Industrial Communication Technology Handbook, Second Edition. CRC Press. pp. 48–1–48–26. ISBN 978-1-4822-0733-0.
- ^ Thomas A. Henzinger; Christoph M. Kirsch (26 September 2001). Embedded Software: First International Workshop, EMSOFT 2001, Tahoe City, CA, USA, October 8-10, 2001. Proceedings (PDF). Springer Science & Business Media. pp. 307–. ISBN 978-3-540-42673-8. Archived (PDF) from the original on 2015-09-22. Retrieved 2015-03-05.
- ^ Yeh, Y.C. (2001). "Safety critical avionics for the 777 primary flight controls system". 20th DASC. 20th Digital Avionics Systems Conference (Cat. No.01CH37219). Vol. 1. pp. 1C2/1–1C2/11. doi:10.1109/DASC.2001.963311. ISBN 978-0-7803-7034-0. S2CID 61489128.
- ^ "ELC: SpaceX lessons learned [LWN.net]". Archived from the original on 2016-08-05. Retrieved 2016-07-21.
- ^ Nanya, T.; Goosen, H.A. (1989). "The Byzantine hardware fault model". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 8 (11): 1226–1231. doi:10.1109/43.41508. ISSN 0278-0070.
- ^ Martins, Rolando; Gandhi, Rajeev; Narasimhan, Priya; Pertet, Soila; Casimiro, António; Kreutz, Diego; Veríssimo, Paulo (2013). "Experiences with Fault-Injection in a Byzantine Fault-Tolerant Protocol". Middleware 2013. Lecture Notes in Computer Science. Vol. 8275. pp. 41–61. doi:10.1007/978-3-642-45065-5_3. ISBN 978-3-642-45064-8. ISSN 0302-9743.
- ^ 미국 특허 7475318, 케빈 R.Driscell, 2009-01-06년 발행, Honeywell International Inc.에 할당.
- ^ Feldman, P.; Micali, S. (1997). "An optimal probabilistic protocol for synchronous Byzantine agreement" (PDF). SIAM J. Comput. 26 (4): 873–933. doi:10.1137/s0097539790187084. Archived (PDF) from the original on 2016-03-05. Retrieved 2012-06-14.
- ^ Paulitsch, M.; Morris, J.; Hall, B.; Driscoll, K.; Latronico, E.; Koopman, P. (2005). "Coverage and the Use of Cyclic Redundancy Codes in Ultra-Dependable Systems". 2005 International Conference on Dependable Systems and Networks (DSN'05). pp. 346–355. doi:10.1109/DSN.2005.31. ISBN 978-0-7695-2282-1. S2CID 14096385.
- ^ Hopkins, Albert L.; Lala, Jaynarayan H.; Smith, T. Basil (1987). "The Evolution of Fault Tolerant Computing at the Charles Stark Draper Laboratory, 1955–85". The Evolution of Fault-Tolerant Computing. Dependable Computing and Fault-Tolerant Systems. Vol. 1. pp. 121–140. doi:10.1007/978-3-7091-8871-2_6. ISBN 978-3-7091-8873-6. ISSN 0932-5581.
- ^ Driscoll, Kevin; Papadopoulos, Gregory; Nelson, Scott; Hartmann, Gary; Ramohalli, Gautham (1984), Multi-Microprocessor Flight Control System (Technical Report), Wright-Patterson Air Force Base, OH: AFWAL/FIGL U.S. Air Force Systems Command, AFWAL-TR-84-3076
- ^ Castro, M.; Liskov, B. (2002). "Practical Byzantine Fault Tolerance and Proactive Recovery". ACM Transactions on Computer Systems. Association for Computing Machinery. 20 (4): 398–461. CiteSeerX 10.1.1.127.6130. doi:10.1145/571637.571640. S2CID 18793794.
- ^ Abd-El-Malek, M.; Ganger, G.; Goodson, G.; Reiter, M.; Wylie, J. (2005). "Fault-scalable Byzantine Fault-Tolerant Services". ACM SIGOPS Operating Systems Review. Association for Computing Machinery. 39 (5): 59. doi:10.1145/1095809.1095817.
- ^ Cowling, James; Myers, Daniel; Liskov, Barbara; Rodrigues, Rodrigo; Shrira, Liuba (2006). HQ Replication: A Hybrid Quorum Protocol for Byzantine Fault Tolerance. Proceedings of the 7th USENIX Symposium on Operating Systems Design and Implementation. pp. 177–190. ISBN 1-931971-47-1.
- ^ Kotla, Ramakrishna; Alvisi, Lorenzo; Dahlin, Mike; Clement, Allen; Wong, Edmund (December 2009). "Zyzzyva: Speculative Byzantine Fault Tolerance". ACM Transactions on Computer Systems. Association for Computing Machinery. 27 (4): 1–39. doi:10.1145/1658357.1658358.
- ^ Guerraoui, Rachid; Kneževic, Nikola; Vukolic, Marko; Quéma, Vivien (2010). The Next 700 BFT Protocols. Proceedings of the 5th European conference on Computer systems. EuroSys. Archived from the original on 2011-10-02. Retrieved 2011-10-04.
- ^ Clement, A.; Wong, E.; Alvisi, L.; Dahlin, M.; Marchetti, M. (April 22–24, 2009). Making Byzantine Fault Tolerant Systems Tolerate Byzantine Faults (PDF). Symposium on Networked Systems Design and Implementation. USENIX. Archived (PDF) from the original on 2010-12-25. Retrieved 2010-02-17.
- ^ Aublin, P.-L.; Ben Mokhtar, S.; Quéma, V. (July 8–11, 2013). RBFT: Redundant Byzantine Fault Tolerance. 33rd IEEE International Conference on Distributed Computing Systems. International Conference on Distributed Computing Systems. Archived from the original on August 5, 2013.
- ^ Bahsoun, J. P.; Guerraoui, R.; Shoker, A. (2015-05-01). "Making BFT Protocols Really Adaptive". Parallel and Distributed Processing Symposium (IPDPS), 2015 IEEE International: 904–913. doi:10.1109/IPDPS.2015.21. ISBN 978-1-4799-8649-1. S2CID 16310807.
- ^ Chun, Byung-Gon; Maniatis, Petros; Shenker, Scott; Kubiatowicz, John (2007-01-01). "Attested Append-only Memory: Making Adversaries Stick to Their Word". Proceedings of Twenty-First ACM SIGOPS Symposium on Operating Systems Principles. SOSP '07. New York, NY, USA: ACM: 189–204. doi:10.1145/1294261.1294280. ISBN 9781595935915. S2CID 6685352.
- ^ Veronese, G. S.; Correia, M.; Bessani, A. N.; Lung, L. C.; Verissimo, P. (2013-01-01). "Efficient Byzantine Fault-Tolerance". IEEE Transactions on Computers. 62 (1): 16–30. CiteSeerX 10.1.1.408.9972. doi:10.1109/TC.2011.221. ISSN 0018-9340. S2CID 8157723.
- ^ Buchman, E.; Kwon, J.; Milosevic, Z. (2018). "The latest gossip on BFT consensus". arXiv:1807.04938 [cs.DC].
- ^ Yamada, Hiroyuki; Nemoto, Jun (2022-03-01). "Scalar DL: scalable and practical byzantine fault detection for transactional database systems". Proceedings of the VLDB Endowment. 15 (7): 1324–1336. doi:10.14778/3523210.3523212. ISSN 2150-8097.