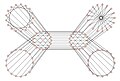
빅스-스미스 그래프
Biggs–Smith graph| 빅스-스미스 그래프 | |
|---|---|
 빅스-스미스 그래프 | |
| 정점 | 102 |
| 가장자리 | 153 |
| 반지름 | 7 |
| 지름 | 7 |
| 둘레 | 9 |
| 자동형성 | 2448(PSL(2,17)) |
| 색수 | 3 |
| 색도 지수 | 3 |
| 특성. | 대칭 거리-정규어 큐빅 해밀턴어 |
| 그래프 및 모수 표 | |
그래프 이론의 수학적 분야에서 Biggs-Smith 그래프는 정점 102개와 가장자리 153개를 가진 3-정규 그래프다.[1]
색도 번호 3, 색도 지수 3, 반지름 7, 직경 7, 둘레 9를 가지고 있다.또한 3-Vertex 연결 그래프와 3-엣지 연결 그래프이기도 하다.
세제곱 거리-정규 그래프는 모두 알려져 있다.[2]Biggs-Smith 그래프는 13개의 그래프 중 하나이다.
대수적 특성
Biggs-Smith 그래프의 자동형성 그룹은 투영 특수 선형 그룹 PSL(2,17)에 대한 2448 이형성[3] 순서의 그룹이다.그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다.따라서 Biggs-Smith 그래프는 대칭 그래프다.그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다.포스터 인구조사에 따르면 F102A로 참조되는 빅스-스미스 그래프는 정점 102에 대한 유일한 입방 대칭 그래프다.[4]
또한 Biggs-Smith 그래프는 인접 행렬의 그래프 고유값 집합인 그래프 스펙트럼에 의해 고유하게 결정된다.[5]
The characteristic polynomial of the Biggs–Smith graph is : .
갤러리
Biggs-Smith 그래프의 색수는 3이다.
Biggs-Smith 그래프의 색지수는 3이다.
Biggs-Smith 그래프의 대체 도면.
Biggs-Smith 그래프를 크기 17의 6 세트로 분해.
참조
- ^ Weisstein, Eric W. "Biggs–Smith Graph". MathWorld.
- ^ 브루워 A. E., 코헨 A. M., 노이마이어 A.거리-일반 그래프.뉴욕: 스프링거-베를라크, 1989.
- ^ 로일, G. F102A 데이터[permanent dead link]
- ^ 콘더, M., 도브사니, P. "삼각형 대칭 그래프 최대 768정점까지." J. 콤빈수학. 콤빈.계산하다.40, 41–63, 2002.
- ^ E. R. 밴 댐 및 W. H. 해머, 일부 거리 정규 그래프의 스펙트럼 특성화.J. 대수학 콤빈. 15, 페이지 189-202, 2003
- 3가 그래프에서, NL Biggs, DH Smith - Bulletin of the London Mathemical Society, 3 (1971) 155-158.
