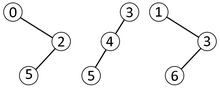
범위 최소 쿼리

Constructing the corresponding Cartesian tree to solve a range minimum query.

범위의 최소 쿼리가 가장 낮은 공통 상위 문제로 감소했습니다.

컴퓨터 과학에서 범위 최소 쿼리(RMQ)는 동등한 객체 배열의 하위 배열에서 최소값을 찾는 문제를 해결합니다.범위 최소 쿼리에는 컴퓨터 과학에서 가장 낮은 공통 상위 문제 및 가장 긴 공통 접두사 문제(LCP)와 같은 몇 가지 사용 사례가 있습니다.

정의.

정수와 같은 완전 순서 집합에서 n개 객체의 $배열$ A $[1 \dots n$ ]가 주어지면 범위 최소 $쿼리 A$ RMQ $(l, r)$ = $최소$ $최소$ 쿼리 A $[k]($ $1µl µk µr µn)$ 는 지정된 하위 $배열$ A $[l$ $\dots r]$ 에서 최소 요소의 위치를 반환합니다.

예를 들어, A = [ $0,5,5,4,3,1,6,3]$ 인 $경우$ 하위 $배열$ A $[3 \dots8]$ = [2 $,5,4,3,1,6]$ 의 범위 최소 쿼리에 대한 답은 A $[7]$ = $1$ 이므로 7입니다.

알고리즘

순진한 해결법

일반적인 설정에서는 $어레이$ A는 정적이며, 즉 일련의 쿼리 중에 요소를 삽입 또는 삭제하지 않고 온라인으로 응답해야 하는 쿼리(즉, 알고리즘에 대해 전체 쿼리 세트를 미리 알 수 없음)이다.이 경우 어레이를 데이터 구조로 전처리하면 쿼리 응답 시간이 단축됩니다.순진한 솔루션은 가능한 모든 쿼리, 즉 A의 $모든$ 서브패키지 최소값을 미리 계산하여 B $[i,$ $j]$ = min $(A [i ... j])$ 이 되도록 $어레이$ B에 저장하면 범위 최소 쿼리는 B에서 $어레이$ 룩업에 의해 일정한 시간에 해결됩니다.length-n 어레이에는 $δ(n²)$ 의 쿼리가 있으며, 이 쿼리에 대한 답변은 ^[1]동적 프로그래밍을 $통해 δ$ (n² $)$ 시간 내에 계산할 수 있습니다.

로그 시간과 선형 공간을 사용한 솔루션

위의 솔루션과 마찬가지로 결과를 미리 계산하여 일정한 시간 내에 질의에 응답할 수 있습니다.단, 어레이에는 모든 요소에 대해 사전 계산된 최소 쿼리와 크기가 2인 범위만 저장됩니다.시작 위치 $i$ 마다 이러한 쿼리가 $δ(log$ n $)$ 있기 때문에 다이내믹 프로그래밍 $테이블$ B의 사이즈는 $δ(n$ $log$ n)이다 $.$ 각 $요소$ B $[i,$ $j]$ 는 A $[i \dots i +2-1 j]$ 범위의 $최소$ 지수를 유지한다.테이블은 반복을^[1] 사용하는 최소값 지수로 채워집니다.

A

[B [i, j-1] a

A

[B [i j -1 +

2,

j-1]

일

경우

,

B

[

i,

j] =

B [i

, j-1

];

그렇지

않으면 B

[i,

j]

=

B [i +2 j -1, j-1]

입니다.

$쿼리 A$ RMQ $(l, r)$ 는 2개의 개별 쿼리로 분할하여 응답할 수 있습니다.하나는 l부터 $r$ 보다 작은 최대 경계까지의 사전 계산된 쿼리입니다.다른 하나는 r이 오른쪽 경계로 $되어$ 있는 같은 길이의 간격에 대한 쿼리입니다.이러한 간격은 중복될 수 있지만, 예를 들어 합계가 아닌 최소값이 계산되기 때문에 이는 문제가 되지 않습니다.이 두 개의 쿼리는 로그 시간으로 응답할 수 있고 남은 것은 두 결과 중 작은 것을 선택하는 것이기 때문에 전체 결과는 로그 시간으로 얻을 수 있습니다.

일정한 시간과 선형 공간을 사용하는 솔루션

시간은 일정하지만 선형 광석 공간 솔루션도 존재합니다.이 아이디어는 로그 시간과 선형 공간을 사용하는 솔루션과 유사합니다.사전 계산된 테이블은 다음과 같이 작성됩니다.

각각에 대해서i에1...n그리고 각각j에1...logn

i+2^{j}<r

+

i+2^{j}<r

<

\displaystyle

i

+2^{j}<r}

RMQ_{A}(i,i+2^{j}-1)

RMQ_{A}(i,i+2^{j}-1)

A

RMQ_{A}(i,i+2^{j}-1)

(

RMQ_{A}(i,i+2^{j}-1)

,

RMQ_{A}(i,i+2^{j}-1)

i +

RMQ_{A}(i,i+2^{j}-1)

j -

RMQ_{A}(i,i+2^{j}-1)

){

displaystyle RMQ_{A}(i,i+

2^{

j}-1)}

를

계산

하여

RMQ_{A}(i,i+2^{j}-1)

합니다.

$RMQ_{A}(l,r)$ 테이블에서는 2개의 $RMQ_{A}(l,l+2^{j}-1)$ $RMQ_{A}(l,l+2^{j}-1)$ $RMQ_{A}(l,r)$ $RMQ_{A}(l,l+2^{j}-1)$ ( $RMQ_{A}(l,l+2^{j}-1)$ $RMQ_{A}(l,r)$ , $RMQ_{A}(l,l+2^{j}-1)$ + $RMQ_{A}(l,l+2^{j}-1)$ - $RMQ_{A}(l,l+2^{j}-1)$ ){ $display$ $style$ RMQ $RMQ_{A}(l,r)$ $_$ { A } ( $l$ , $RMQ_{A}(l,r)$ l + 2 j - 1 ){ display $style$ RMQ _ { $A$ $RMQ_{A}(l,l+2^{j}-1)$ } ( $l$ , $l$ + 2 $RMQ_{A}(l,l+2^{j}-1)$ ^ { $J$ - $1$ } $RMQ_{A}(r-2^{j}+1,r)$ r r r r $RMQ_{A}(r-2^{j}+1,r)$ two two two two two two two RMQ A $candisplaydisplay1displaydisplaydisplay$ by by by by by by by by by by by by by by by 。

이러한 2개의 서브쿼리 중 하나에 원래 쿼리에 대한 응답이 포함되어 있는 이유는 $[l,r]$ 범위 $[l,r]$ [ $l$ $[l,r]$ r $]{displaystyle [l$ $[l,l+2^{k}-1]$ $[l,r]$ $[l,r]$ $displaystyle$ [ $l,$ $[l,r]$ $2^{k}-1}$ $displaystyle$ k $}$ 가 $k$ $[l,l+2^{k}-1]$ 항상 $[l,r]$ 하기 때문입니다 $.$ $playstyle [l,r$ 이것은 모순으로 쉽게 증명될 수 있습니다.만약 존재하는 정수 k{k\displaystyle}은 그것의 최대 수이는 a=l+2k<>을 만족시키며{\displaystyle l+2^{k}&lt하며}과 범위[는 a=l+2k− 1l,]{\displaystyle[l,l+2^{k})]}, 그때[는 a=l+2k l,+1− 1]범위[l, r]{\displaystyle[l,r]}의 절반을 차지할 수 없{\displayst.yle는 경우l $,l+2^{k+1}-1]$ 은 $[l,l+2^{k+1}-1]$ $l+2^{k}<r$ 는 $r$ $r$ 을 $넘지$ 않고 범위의 절반 이상을 커버할 수 있습니다.그러면 $k$ + $l+2^{k}<r$ $l+2^{k}<r$ \ $displaystyle$ l + $2^$ { $k$ } < $r$ $l+2^{k}<r$ 는 $k$ 을 $k$ $k+1$ $l+2^{k}<r$ 시키는 최대수가 $k+1$ k $k+1$ + $k+1$ \ $displaystyle$ k+ $1$

A = [

0,5,

2,

5,4,3,1,6,3]

에

대한

결과 표

		$k$
		0	1	2	3
$l$	1	1	1	1	1
	2	2	3	3	7
	3	3	3	3	7
	4	4	5	6	7
	5	5	6	7	7
	6	6	7	7	7
	7	7	7	7	7
	8	8	7	7	7
	9	9	7	7	7

로그 시간과 선형 공간을 사용한 솔루션

이 솔루션은 O $(log$ n $)$ $시간$ 내에 RMQ에 응답합니다.데이터 구조는 O $(n)$ 공간을 $사용$ 하며 데이터 구조도 일정한 시간에 쿼리에 응답하는 데 사용할 수 있습니다.배열된 첫번째 개념적으로 크기의 블록).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}로 나뉜다.Mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}log n/4.그런 다음 각 블록의 최소값을 전체적으로 O $(n)$ 시간으로 $계산$ 할 수 있으며 최소값은 새 배열에 저장됩니다.

RMQ는 왼쪽 쿼리 경계, 오른쪽 쿼리 경계 및 그 사이의 모든 블록을 포함하는 블록을 조사함으로써 로그 시간 내에 응답할 수 있습니다.

경계를 포함하는 2개의 블록은 간단하게 검색할 수 있습니다.경계 밖의 요소는 살펴볼 필요도 없습니다.이것은 로그 타임으로 할 수 있다.
쿼리에 응답하려면 범위에 완전히 포함된 모든 블록의 최소값과 위에서 언급한 두 개의 최소값을 비교해야 합니다.
배열이 로그 $n$ / $4$ $크기$ 의 블록으로 분할되었기 때문에 쿼리에 완전히 포함된 블록은 최대 $4n / log$ n개입니다.
선형 결석 솔루션을 사용하면 이들 블록의 전체 최소값을 구할 수 있습니다.이 데이터 구조의 $크기$ 는 O $(n / log$ $n$ log ( $n / log$ n $))$ = $O (n)$ 입니다.
이제 3개의 최소값만 비교하면 됩니다.

예를 들어 $어레이$ A = [ $0,5,5,4,3,1,6,3]$ 및 블록 크기 3을 사용하면 최소 $어레이$ A $'$ = [ $0,3,1]$ 이 생성됩니다.

일정한 시간과 선형 공간을 사용하는 솔루션

위의 솔루션을 사용하더라도 쿼리에 완전히 포함되지 않은 블록 내의 서브쿼리는 일정 시간 내에 응답해야 합니다.이러한 블록에는 최대 $2개$ 의 블록이 있습니다.l을 포함하는 블록과 r을 $포함$ 하는 블록입니다.일정한 시간은 배열의 모든 블록에 대한 데카르트 트리를 저장함으로써 얻을 수 있습니다.몇 가지 관찰:

동형 데카르트 트리가 있는 블록은 해당 블록의 모든 쿼리에 대해 동일한 결과를 제공합니다.
s 노드의 $다른$ 데카르트 트리의 $수$ 는_s c, s'번째 카탈로니아 수이다.
따라서 블록에 대한 다른 데카르트 나무의 수는 4개 범위 $내$ 에^s 있습니다.

이러한 모든 트리에 대해 모든 쿼리에 대해 가능한 결과를 저장해야 합니다.이는 결국 $또는$ O $(log 2$ n $)$ 엔트리로 $귀결$ 됩니다².이는 테이블의 전체 크기가 O $(n) 임$ 을 의미합니다.

결과를 효율적으로 검색하려면 특정 블록에 해당하는 데카르트 트리(행)를 일정 시간 내에 주소 지정할 수 있어야 합니다.솔루션은 모든 트리의 결과를 배열에 저장하고 이진수 트리에서 정수까지의 고유한 투영을 찾아 엔트리를 처리하는 것입니다.이는 트리에서 너비 우선 검색을 수행하고 리프 노드를 추가하여 데카르트 트리의 모든 기존 노드에 정확히 두 개의 하위 노드가 생기도록 함으로써 달성할 수 있습니다.다음으로 모든 내부 노드를 0비트로 나타내며 모든 리프를 1비트로 비트워드로 나타내면(레벨 순서로 트리를 다시 통과함으로써) 정수가 생성됩니다.이로 인해 모든 트리의 $로그$ n/4 $크기$ 가 됩니다.임의의 트리에 대한 랜덤 액세스를 일정 시간 내에 활성화하려면 원래 어레이에 포함되지 않은 트리도 포함해야 합니다. $log$ n $/ 4비트$ $길이$ 의 인덱스를 가진 배열의 $크기$ 는^{log n/4} 2 = $O (n)$ 입니다.

A = [

0,

5,2,

5,4,3

,1

,6,3]

에

대한

데카르트 나무의 예.첫 번째와 세 번째 트리는 레이아웃이 같기 때문에 왼쪽 테이블에는 정확히 2개의 사전 계산된 쿼리 세트가 있습니다.

A = 세

개의 데카르트 블록 트리에 대한 사전

계산된 결과 [

0

,5,5,4,3,1,6

,3]

색인	1			2			3
색인	1	2	3	1	2	3	1	2	3
0	—
23(비트워드 0010111)	1	2	3	—	2	3	—	—	3
39(비트워드 0100111)	1	1	1	—	2	3	—	—	3
127	—

적용들

RMQ는 정확하고 대략적인 문자열 매칭에서 많은 작업을 위한 도구로 사용됩니다.Fischer와 Heun(2007)^[2]^{: 3}에서 몇 가지 응용 프로그램을 찾을 수 있습니다.

트리에서 가장 낮은 공통 조상 계산

RMQ는 가장 낮은 공통 상위^[1]^[3] 문제를 해결하기 위해 사용할 수 있으며 정확하고 대략적인 문자열 매칭에서 많은 작업을 위한 도구로 사용됩니다.루트 $트리$ S = ( $V,$ $E)$ 및 2개의 $노드$ v, $w$ a V의 LCA $쿼리 S LCA ($ v, w)는 루트에서 $w$ 로 경로의 가장 깊은 $노드$ u(v $또는$ $w일$ 수 있음)를 $반환$ 하고 v. Gabow, Bentley 및 Tarjan(1969)은 LCA 문제를 선형 시간 내에 줄일 수 있음을 보여 줍니다.따라서 RMQ 문제와 마찬가지로 LCA 문제도 일정한 시간과 ^[2]선형 공간에서 해결할 수 있습니다.

문자열에서 가장 긴 공통 접두사 계산

텍스트 인덱싱의 경우 RMQ를 사용하여 LCP(최장 공통 프레픽스)를 찾을 수 있습니다. $LCP T (i,$ $j)$ 는 T의 $인덱스$ i 및 $j$ 에서 시작하는 접미사의 LCP를 계산합니다.이를 위해 먼저 접미사 $배열$ A와 역접미사 $배열 -1$ A를 계산합니다.그런 다음 A에서 $인접$ 한 접미사의 LCP를 제공하는 LCP $배열$ H를 계산합니다.이러한 데이터 구조가 계산되고 RMQ 전처리가 완료되면 일반 LCP의 길이는 $LCP(i,$ $j)$ = $RMQ H (A -1 [i]$ + $1 -1,$ $A[j])$ 의 공식에 의해 일정 시간 내에 계산할 수 있습니다.여기서 A $[i -1]$ + 1 < = $A [$ j](스왑)^[4]의^-1 단순성을 가정합니다.

「」를 참조해 주세요.

범위 쿼리(데이터 구조)

레퍼런스

Berkman, Omer; Vishkin, Uzi (1993). "Recursive Star-Tree Parallel Data Structure". SIAM Journal on Computing. 22 (2): 221–242. doi:10.1137/0222017. Archived from the original on September 23, 2017.
Johannes Fischer (Dec 2009). Optimal Succinctness for Range Minimum Queries (Technical Report). Universität Tübingen, Center for Bioinformatics. arXiv:0812.2775. Bibcode:2008arXiv0812.2775F.

^ ^a ^b ^c Bender, Michael A.; Farach-Colton, Martín; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2005). "Lowest common ancestors in trees and directed acyclic graphs" (PDF). Journal of Algorithms. 57 (2): 75–94. doi:10.1016/j.jalgor.2005.08.001.
^ ^a ^b Fischer, Johannes; Heun, Volker (2007). "A New Succinct Representation of RMQ-Information and Improvements in the Enhanced Suffix Array". Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. Proceedings of the International Symposium on Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. LNCS. Vol. 4614. Springer. pp. 459–470. doi:10.1007/978-3-540-74450-4_41. ISBN 978-3-540-74449-8.
^ Bender, Michael; Farach-Colton, Martín (2000). "The LCA Problem Revisited". LATIN 2000: Theoretical Informatics. LATIN 2000: Theoretical Informatics. LNCS. Vol. 1776. Springer. pp. 88–94. doi:10.1007/10719839_9. ISBN 978-3-540-67306-4.
^ Fischer, J. and V. Heun (2006). "Theoretical and practical improvements on the RMQ-problem, with applications to LCA and LCE". Combinatorial Pattern Matching. Lecture Notes in Computer Science. Vol. 4009. pp. 36–48. CiteSeerX 10.1.1.64.5439. doi:10.1007/11780441_5. ISBN 978-3-540-35455-0. {{cite book}}:누락 또는 비어 있음 title=(도움말)

외부 링크

[bender-jalg-1] Bender, Michael A.; Farach-Colton, Martín; Pemmasani, Giridhar; Skiena, Steven; Sumazin, Pavel (2005). "Lowest common ancestors in trees and directed acyclic graphs" (PDF). Journal of Algorithms. 57 (2): 75–94. doi:10.1016/j.jalgor.2005.08.001.

[fischer07-2] Fischer, Johannes; Heun, Volker (2007). "A New Succinct Representation of RMQ-Information and Improvements in the Enhanced Suffix Array". Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. Proceedings of the International Symposium on Combinatorics, Algorithms, Probabilistic and Experimental Methodologies. LNCS. Vol. 4614. Springer. pp. 459–470. doi:10.1007/978-3-540-74450-4_41. ISBN 978-3-540-74449-8.

[3] Bender, Michael; Farach-Colton, Martín (2000). "The LCA Problem Revisited". LATIN 2000: Theoretical Informatics. LATIN 2000: Theoretical Informatics. LNCS. Vol. 1776. Springer. pp. 88–94. doi:10.1007/10719839_9. ISBN 978-3-540-67306-4.

[10.1007/11780441_5-4] Fischer, J. and V. Heun (2006). "Theoretical and practical improvements on the RMQ-problem, with applications to LCA and LCE". Combinatorial Pattern Matching. Lecture Notes in Computer Science. Vol. 4009. pp. 36–48. CiteSeerX 10.1.1.64.5439. doi:10.1007/11780441_5. ISBN 978-3-540-35455-0. {{cite book}}:누락 또는 비어 있음 title=(도움말)

[1]

[2]

[3]

[4]

Search

범위 최소 쿼리

네임스페이스

더

목차

정의.

알고리즘

순진한 해결법

로그 시간과 선형 공간을 사용한 솔루션

일정한 시간과 선형 공간을 사용하는 솔루션

로그 시간과 선형 공간을 사용한 솔루션

일정한 시간과 선형 공간을 사용하는 솔루션

적용들

트리에서 가장 낮은 공통 조상 계산

문자열에서 가장 긴 공통 접두사 계산

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

범위 최소 쿼리

정의.

알고리즘

순진한 해결법

로그 시간과 선형 공간을 사용한 솔루션

일정한 시간과 선형 공간을 사용하는 솔루션

로그 시간과 선형 공간을 사용한 솔루션

일정한 시간과 선형 공간을 사용하는 솔루션

적용들

트리에서 가장 낮은 공통 조상 계산

문자열에서 가장 긴 공통 접두사 계산

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.