다극 교환 상호 작용

LaFeAsO,^[1][2] PrFeP₄₁₂,^[3][4] YbRuGe₂₂,^[5] UO₂,^{[6][7][8][9][10]} NpO₂,^[11][12][13] CeLaB_1−xx6,^[14] URuSi₂₂^{[15][16][17][18][19]} 및 기타 많은 화합물 등 스핀-오빗 상호작용이 강한 자성물질은 상위 다극(예: 4배, 8배)^[20]으로 구성된 자기질서를 가지고 있는 것으로 밝혀졌다.스핀-오빗 결합이 강하기 때문에 총 각운동량 양자수 J가 1/2보다 클 때 다중극이 시스템에 자동으로 도입된다.이러한 다중극이 어떤 교환 메커니즘에 의해 결합되는 경우, 이러한 다중극은 일반적인 스핀 1/2 하이젠베르크 문제와 같은 순서를 갖는 경향이 있다.다극 순서를 제외하고, 많은 숨겨진 순서 현상은 다극 상호작용과 밀접하게 관련되어 있다고 믿어진다.

텐서 연산자 확장

기본 개념

힐버트 공간이 j${\displaystyle ,}$ ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$ {\$displaystyle$ j$,m_{j}\rangle$ $\}$로 확장된 양자역학 시스템을 고려합니다. $여기$서$$j {\$displaystyle$ j$}$는 총 각운동량이고 $m{\displaystyle {}_{}}$ {\$displaystyle m_{j}}$는 양자화 축에 투영된 것입니다.다음으로 기본 집합${\displaystyle }${${\displaystyle j,}$ ${\displaystyle m_{}}$ j $}{displaystyle \lbrace$ j$,m_{j}\rangle \rbrace}$을$({\displaystyle }$를) 차원 (${\displaystyle \mathrm{2j}}$+${\displaystyle 1}$)$${$displaystyle (2j + 1$의 행렬로 사용하여 양자 연산자를 나타낼 수 있습니다.따라서 (${\displaystyle 2}$j +${\displaystyle {}^{}1}$) ${\displaystyle {2\mathrm{}}^{}}${{$displaystyle (2j+1)^{2}}$ 행렬을${\displaystyle }$정의하여 이 힐베르트 공간에서 양자 연산자를 완전히 확장할 수 있습니다.J=1/2를 예로 들면, 양자 연산자 A는 다음과 같이 확장할 수 있다.

${\displaystyle A=bgin{bmatrix}1&2\\3&4\end{bmatrix}=1{\begin{bmatrix}+2{\begin{bmatrix}+3\begin{bmatrix}&1&0\1}$

$행렬{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{Li}}_{}}$ j $=$ ${\displaystyle i}$ $j$ j { $displaystyle$L_{$ij}= i\$rangle \$sublle$ j $}$는 연산자 공간에서 기본 집합을 형성합니다.이 Hilbert에 정의된 양자 연산자는 { ${\displaystyle L_{}}$ ${\displaystyle i_{}}$ j$$ { $displaystyle$\ $lbrace L_{ij}\rbrace }$ 연산자에${\displaystyle }$의해 확장될 수 있습니다.다음에서는 이러한 행렬을 양자 상태의 고유 기저를 구별하기 위한 슈퍼 기법으로 부르자.위의 슈퍼베이스 {${\displaystyle {\mathrm{Li}}_{}}$ j $}({displaystyle \lbrace L_{ij}\rbrace$})는 상태 $({displaystyle i\$rangle$})$와$$j({$displaystyle j\$rangle$\})$ 간의 천이를 나타내기 때문에 천이 슈퍼베이스라고 할 수 있습니다.실제로만 존재하는 것은 아닙니다.우리는 또한 파울리 행렬과 항등 행렬을 사용하여 슈퍼 베이스를 형성할 수 있다.

${\displaystyle A={\begin{bmatrix}1&, 2\\3&, 4\end{bmatrix}}={\frac{5}{2}}{\begin{bmatrix}1&, 0\\0&, 1\end{bmatrix}}+{\frac{나는}{2}}{\begin{bmatrix}0&, i\\-i&, 0\end{bmatrix}}+{\frac{3}{2}}{\begin{bmatrix}-1&, 0\\0&, 1\end{bmatrix}}+{\frac{5}{2}}{\begin{bmatrix}0&, 1\\1&, 0\end{bmatrix}}={\frac{5}{2}}I+{\frac{나는}{2}}\sigma_{y.}+{\frac{3}{2}}\sigma{2_{z}+{\frac{5}}}\syslog _{x}}$

${\displaystyle x_{}}$x , ${\displaystyle y_{}}$y , ${\displaystyle z_{}}$z \ $displaystyle$\ $sigma$_ {$x$ , \ $sigma$_ { $y$, \ $sigma$_ { $z$}의$$ 회전 특성은 입방 $고조파{\displaystyle {}_{}}$ ${\displaystyle T_{}}$x , ${\displaystyle {}_{}{y}_{}}$ , ${\displaystyle {}_{}}$ \ $displaystyle$ T_ ${$$x$ }의 랭크 1 텐서와 같은 규칙을 따릅니다.$T_{y}, T_{z}$ 및$$ ID $매트릭스{\displaystyle }$I(\$displaystyle$ I$)$는 0 텐서 $(\$$s$$\})$와 동일한 규칙을 따릅니다.기본 집합 $\{{\displaystyle }$ ${\displaystyle I}$、 ${\displaystyle x_{}}$ x${\displaystyle {}_{}}$、 ${\displaystyle y_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle z_{}}$ z ${\displaystyle {}_{}}$（ \ $displaystyle$\$lbrace$ I , \ $sigma _ x$} ）$。$또 다른 일반적으로 사용되는 슈퍼베이스는 구면 고조파 슈퍼베이스입니다.이 슈퍼베이스는 "x", "$\$ _{x$}\sigma$ _${y}"$를 "${\displaystyle I",}$ ${\displaystyle {"-1}_{}}$ "$0$ (\$displaystyle$ \$lbrace$I,\$sigma_1), _0sigma_0+{1}$로 치환하여 구축됩니다.

${\displaystyle A={\begin{bmatrix}1&, 2\\3&, 4\end{bmatrix}}={\frac{5}{2}}{\begin{bmatrix}1&, 0\\0&, 1\end{bmatrix}}+2{\begin{bmatrix}0&, 1\\0&, 0\end{bmatrix}}+{\frac{3}{2}}{\begin{bmatrix}-1&, 0\\0&, 1\end{bmatrix}}-3{\begin{bmatrix}0&, 0\\-1&, 0\end{bmatrix}}={\frac{5}{2}}I+2\sigma _{+1}+{\frac{3}{2}}\sigma _{0}-3\sigma_{.-1}}$

다시${\displaystyle {}_{}}\theta {\displaystyle {}_{}}$ -${\displaystyle {}_{}{1}_{}}$ , ${\displaystyle {\theta \mathrm{}}_{}}$0 ,${\displaystyle {\mathrm{\theta }}_{}}$+ 1 (\$displaystyle \sigma$ _${-1},\sigma _{+1})$은 랭크 1 구형 고조파 $텐서{\displaystyle {}_{}^{}}$Y -${\displaystyle {\mathrm{}}_{}^{}}$, ${\displaystyle {Y\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}^{}}$, ${\displaystyle {}_{}^{}{}_{}^{}}$- ${\displaystyle {\mathrm{}}_{}^{}}$(\$displaystyle$Y _ {-$1}^{$1}와 같은 회전 특성을 공유합니다.$Y_{0}^{1}, Y_{-1}^1$ 그래서 구면 초염기라고 한다.

$원자궤도{\displaystyle s,}$ ${\displaystyle p,}$ $,$ f(\$displaystyle$ s,$p, d,$f)도$$ 구면 또는 입방체 조화 함수로 기술되기 때문에 본질적으로 공간 함수가 아닌 행렬이지만 원자궤도의 파동 함수를 사용하여 이러한 연산자를 상상하거나 시각화할 수 있다.

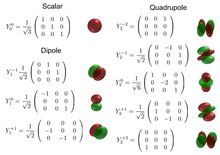
문제를 J ${\displaystyle =}$ ${\displaystyle 1}(\backslash$$displaystyle$ J$=1)$로 확장하면 슈퍼 베이스를 형성하기 위해 9개의 매트릭스가 필요합니다.전이 슈퍼베이스에는 { ${\displaystyle L_{}}$ ${\displaystyle i_{}}$j ;${\displaystyle i}$ , j ${\displaystyle =1}$ ~ ${\displaystyle 3}$ $}$ { $displaystyle \lbrace L_{ij}$ ;$i$ , j$= 1$ \$sim$3 \$rbrace$ $\}$${\displaystyle }$이 있습니다.입방 슈퍼베이스에는 { ${\displaystyle T_{}}$s , ${\displaystyle {}_{}{x}_{}}$ , ${\displaystyle T_{}}$ Y${\displaystyle {}_{}}$, ${\displaystyle T_{}{}_{}{Z}_{}}$ , ${\displaystyle T_{}}$ - 2${\displaystyle {{}^{}{Z\mathrm{}}^{}}_{}{}_{}}$} ${\displaystyle {}_{}}$ 있습니다.$T_{y}, T_{z}, T_{xy},$$T_{yz}, T_{zx}, T_{x^{2}-y^{2}, T_{3z^{2}-r^{2}}\rbrace$ 구면 슈퍼베이스로는 {${\displaystyle {\mathrm{}}_{}^{}}$ 0${\displaystyle {}_{}^{}{}_{}^{}{}_{}^{}}$ - ${\displaystyle {}_{}^{}}$ ${\displaystyle {\mathrm{Y}}_{}^{}}$ - ${\displaystyle {}_{,}^{}}$ ${\displaystyle {\mathrm{Y}}_{}^{}}$- ${\displaystyle {\mathrm{}}_{}^{}}$, Y - 2${\displaystyle {,}_{}^{}}$ Y - ${\displaystyle {\mathrm{}}_{}^{}{}_{}^{}}$ ${\displaystyle {Y\mathrm{}}_{}^{}}$ - ${\displaystyle {}_{}^{}}$가 있다.$Y_{0}^{1}, Y_{-1}^{1}, Y_{-2}^2}, Y_{-1}^{2},$$Y_{0}^{2},$$Y_{1}^{2},$$Y_{2}^{2}\rbrace$ 그룹 이론에서 ${\displaystyle T_{}s{}_{}^{}}$ / ${\displaystyle {Y\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$0 ({$display style$ T_${$$s}/Y_{0}^0}}$은 스칼라 또는 랭크0 텐서, ${\displaystyle T_{}}$ x${\displaystyle {,}_{}}$ ${\displaystyle y_{}}$z${\displaystyle {}_{}}$ /${\displaystyle {}_{}^{}Y{}_{}^{}}$ -${\displaystyle 1_{}^{}}$, 0${\displaystyle {,}_{}^{}}$ +$$ (\$display style T_x, yz}/0)이라고 불립니다.$${\displaystyle {,}_{}^{}}$ - ${\displaystyle 1_{}^{}}$, 0${\displaystyle {,}_{}^{}}$ +${\displaystyle 1_{}^{}}$,${\displaystyle {}_{}^{}}$+ ${\displaystyle 2_{}^{}}$({$xy,yz,zx,x^{2}-y^{2}-r^{2})/Y_{-2,-1,0,+2,+2}^{2}^{$2}}는$$ 4극 또는 랭크2 ^[20]텐서라고 불립니다.

이 예에서는 J$(\displaystyle$ J$)$ - 멀티플릿$$ $문제$의 경우 완전한 슈퍼 베이스를 형성하려면 0${\displaystyle ~2}J{\displaystyle \mathrm{}}$(\$displaystyle$0\$sim$ 2J$$$)$ 텐서 연산자가 모두 필요합니다.$따라서{\displaystyle }$ J ${\displaystyle =}$ {$displaystyle$ J$=1}$시스템의$$ 경우 밀도 매트릭스에 4극 성분이 있어야 합니다.이것이 J> / $(\displaystyle$ J $> 1$/2$) 문제$가 시스템에 멀티폴을 자동으로 도입하는 이유입니다.

정식 정의

$J{\displaystyle }${\$displaystyle$ J$}$ - 멀티플릿$$ 문제의 구면 고조파 슈퍼베이스의 일반적인 정의는 다음과 같이 나타낼 수 있습니다.

${\displaystyle Y_{K}^{Q}(J)=\sum _{MM^{\prime}}(-1)^{J-M}(2K+1)^2}\times \leftfilename\filename {filename}J&K^{{\prime }}\M^{{\prime}}}\M&Q\end{matrix}\right) JM\rangle JM^{{\prime }},$

여기서 괄호는 3-j 기호를 나타내고, K는 0$~$(\$displaystyle$ 0$\sim$ 2J$),$ $Q$는 -K ~ +K 범위의 K 등급의 투영 지수입니다.모든 텐서 연산자가 에르미트인 입방체 고조파 슈퍼 베이스는 다음과 같이 정의될 수 있다.

${\displaystyle T_{K}^{Q}=blac {1}{\displayrt {2}}[(-1)^{Q}Y_{K}^{Q}(J)+Y_{K}^{-Q}(J)}$

${\displaystyle T_{K}^{-Q}=param frac {i}{\paramrt {2}}[Y_{K}^{-Q}(J)-(-1)^{Q}Y_{K}^{-Q}(J)}$

$그런{\displaystyle }$ 다음 J$${\$displaystyle$ J$}$ - 멀티플릿$$ 힐버트 공간에 정의된 $양자{\displaystyle }$ 연산자$$A {\$displaystyle$ A$}$는 다음과 같이 확장할 수 있습니다.

${\displaystyle A=\sum _{K,Q}\alpha _{K}^{Q}Y_{K}^{Q}=\sum_{K,Q}\beta_{K}^{Q}T_{K}^{Q}=\sum_{i,j}\sum_{i,j}L_{i,j}$

여기서 확장 계수는 ${\displaystyle \alpha }$ ${\displaystyle K}$ Q${\displaystyle }$= ${\displaystyle T_{}^{}}$ r [ A Y ${\displaystyle {}_{}^{}}$ Q${\displaystyle {}_{}^{}{†}_{}^{}}$ $]$ \ $displaystyle \alpha$_ {$K}^{Q$} $= Tr[$${\displaystyle 와}$ $같이{\displaystyle {}_{}^{}}$ 미량 내적을 취함으로써 얻을 수 있다.$AY_{K}^{Q\dagger$ 이들 연산자를 선형으로 조합하여 대칭이 다른 새로운 슈퍼 베이스를 형성할 수 있다고 합니다.

다중 교환 설명

텐서 연산자의 덧셈 정리를 사용하여, 순위 n 텐서와 순위 m 텐서의 곱은 순위 n+m ~ n-m의 새로운 텐서를 생성할 수 있다.따라서, 높은 등급의 텐서는 낮은 등급의 텐서의 곱으로 표현될 수 있다.이 규칙은 높은 순위의 다극 교환 항을 쌍극자(또는 의사 교환)의 "다중 교환" 공정으로 해석하는 데 유용합니다.예를 들어, ${\displaystyle \mathrm{J}}$ $=$ 1 {\$displaystyle J=$1$$} $케이스$의 구면 고조파 텐서 연산자의 경우, 다음과 같이 한다.

${\displaystyle Y_{2}^{-2}=2Y_{1}^{-1}Y_{1}^{-1}$

${\displaystyle Y_{2}^{-1}=sqrt {2}}(Y_{1}^{1}Y_{1}^{0}+Y_{1}^{0}Y_{1}^{-1}}$

${\displaystyle Y_{2}^{0}=sqrt {24}/6(Y_{1}^{-1}Y_{1}^{+1}+2Y_{1}^{0}Y_{1}^{0}+Y_{1}^{+1}Y_{1}^{-1}}$

${\displaystyle Y_{2}^{+1}=sqrt {2}}(Y_{1}^{0})Y_{1}^{+1}+Y_{1}^{+1}Y_{1}^{0}}$

${\displaystyle Y_{2}^{+2}=2Y_{1}^{+1}Y_{1}^{+1}}$

그렇다면 4극-4극 상호작용(다음 섹션 참조)은 2단계 쌍극-쌍극 상호작용으로 간주할 수 있다.$예$를 들어 ${\displaystyle {Y{\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {2_{}}_{}^{}}$i + ${\displaystyle {{\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {i_{}}_{}^{}}$ ${\displaystyle {Y{\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {2_{}}_{}^{}}$j - ${\displaystyle {2_{}}_{}^{}}$ j ${\displaystyle {{}_{}}_{}^{}}$ ${\displaystyle 4}$ ${\displaystyle {Y{\mathrm{}}_{}}_{}^{}}$ 1${\displaystyle {{}_{}}_{}^{i_{}}}$ + ${\displaystyle {{}_{}}_{}^{}{}_{}^{}}$ ${\displaystyle {i{\mathrm{}}_{}}_{}^{}}$ 1${\displaystyle {{}_{}}_{}^{i_{}}}$ + ${\displaystyle {{\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {i_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}{}_{}^{}}$ ${\displaystyle {1{\mathrm{}}_{}}_{}^{}{{}_{}}_{}^{}{j_{}}_{}^{}}$- ${\displaystyle {{\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}{}_{}^{}}$ - ${\displaystyle {1_{}}_{}^{}}$ j$${ $display Y$_ { $2$_ { i$}^{ 2$_ {$$$i$ }}$Y_{2_{j}}^{-2_{j}}=4$$Y_{1_{i}}^{+1_{i}}$$Y_{1_{i}}^{+1_{i}}$$Y_{1_{j}}^{-1_{j}}$$Y_{1_{j}^{-1_{j$ 사이트$i$의 1단계 4극 $이행{\displaystyle {}_{}^{}}$ ${\displaystyle {{\mathrm{}}_{}}_{{}_{}}^{}}$+ ${\displaystyle {{2i}_{}}_{}^{}}${{$displaystyle$Y_${$$i}^{+2_{i$}}^{$displaystyle$ i$}$의 2단계 $쌍극{\displaystyle {}_{}^{}}$ ${\displaystyle {{이행}_{}}_{}^{}}$ $+$}^{$displaystyle$ Y_1}^{i}}^{$1}^{$i}}}^2+1}^{i}}^{i}}}}^2_i}^2+1}}^2_i}}^2_i}^2_i}$Y_{1_{i}}^{+1_{i$ 따라서 사이트 간 교환뿐만 아니라 사이트 간 교환 용어(멀티 교환)도 표시됩니다.$(\displaystyle$ J$)$가 더 크면 더 복잡한 사이트 내 교환 용어가 나타날 것으로 예상할 수 있습니다.그러나, 이것은 섭동 확장이 아니라 단지 수학적 기법이라는 것을 주목해야 한다.상위 항이 하위 항보다 작을 필요는 없습니다.많은 시스템에서는 하위 용어보다 상위 ^[20]용어가 더 중요합니다.

다극 교환 상호 작용

시스템에서 ^[20]두 자기 모멘트 간의 교환 상호작용을 유도하는 4가지 주요 메커니즘이 있습니다.1).직접 교환 2)RKKY 3)초변화 4).스핀래티스어떤 것이 지배적이든, 교환 상호작용의 일반적인 형태는 다음과 같이 기술될^[21] 수 있다.

${{displaystyle H=\sum _{ij}\sum _{KQ}C_{K_{j}}^{Q_{i}Q_{j}}T_{K_{i}}^{Q_{i}}T_{K_{j}}^{Q_{j}}}$

$여기$서 i${\displaystyle ,}$ $({displaystyle i,$j$$}는 사이트 인덱스, ${\displaystyle {C{}_{}}_{}^{}}$ ${\displaystyle {Ki}_{}^{}}$ K j ${\displaystyle {Q_{}}_{}^{}}$ $({$는 두 개의 다극 $모멘트{\displaystyle {}_{}^{}}$ ${\displaystyle {{TKi}_{}}_{}^{}}${\$displaystyle$ T_K_${j$}}{i}}^{i$}}}{$i}}}{i}}}}{i}}}}}{i}}}}}}}{i}}}}}{i}}}}}}}}}{i}}}$K를$$$1로 $제한$하면 해밀턴이 기존 하이젠버그 모델로 환원된다는 것을 바로 알 수 있다.

다극 교환 해밀턴의 중요한 특징은 이방성이다.^[21]결합 $상수{\displaystyle {}_{}^{}}$ ${\displaystyle {C{}_{}}_{}^{}}$ ${\displaystyle {K_{}}_{}^{}}$ i ${\displaystyle {K_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$ ${\displaystyle Q_{}^{}}$ ${\displaystyle {j_{}}_{}^{}}$ {$displaystyle C_{K_{i}K_{j}}^{Q{i}Q_{j}}$의 값은 보통 두 멀티폴 사이의 상대 각도에 매우 민감합니다.결합 상수가 균질 시스템에서 등방성이라는 기존의 스핀 전용 교환 해밀턴과는 달리, 시스템의 자기 모멘트에 결합하는 고이성 원자 궤도($s{\displaystyle ,}$ ${\displaystyle p,}$ ${\displaystyle d,}$ $(\displaystyle$ s$, p$, $d, f)$의 형태를 호출)는 균질에서도 큰 이방성을 야기할 수밖에 없다.s 시스템.이것이 대부분의 다극 순서가 비콜리네어인 주요 이유 중 하나입니다.

다극 모멘트의 반강자성

강자성 구성에서 이웃하는 두 부위의 자화축을 플립함으로써 반강자성을 정의할 수 있는 자기 스핀 순서와 달리 다극의 자화축 플립은 보통 의미가 없다.${\displaystyle {예}_{}}$를 들어 ${\displaystyle {\mathrm{Ty}}_{}}$z(\$displaystyle T_{yz$$})$ 모멘트를 예로 들어$,$ $display(\displaystyle$ \pi$$$)$ 회전으로 z축을 y축 방향으로 플립해도 변경되지 않습니다.따라서 반강자성 다극성 순서의 권장 정의는^[21] $§$ ${\displaystyle$ \pi$\},$ $즉{\displaystyle }$ 위상을 반전시키는 것입니다.${\displaystyle {\mathrm{Ty}}_{}}$ z ${\displaystyle {}_{}}$ ${\displaystyle e^{}}$ ${\displaystyle {}^{}{}_{}}$ ${\displaystyle {\mathrm{Ty}}_{}}$ z $=$ - ${\displaystyle {\mathrm{Ty}}_{}}$z \ $displaystyle T_{yz }\rightarrow e^{i\pi }T_{$yz$\}.$ 이 점에서 반강자성 스핀 순서는 이 정의의 특수한 경우이며, 즉 쌍극자 모멘트를 뒤집는 것이다.상위 멀티폴의 경우, 예를 들어${\displaystyle {\mathrm{Ty}}_{}}$ z$(\$는 실제로는${\displaystyle }\theta {\displaystyle }$ /$$(\$displaystyle \pi /2})$ 회전이며$$, ${\displaystyle {{}^{}}_{}}$ ${\displaystyle {{z\mathrm{}}^{}}_{}}$2 - ${\displaystyle {{r\mathrm{}}^{}}_{}}$ 2$(\$의 경우 $회전$도 아닙니다.

결합 상수 계산

다극 교환 상호작용의 계산은 많은 측면에서 여전히 어려운 문제이다.해밀턴 모델을 실험에 적합시키는 것에 기초한 많은 연구가 있었지만, 제1원칙 체계에 기초한 결합 상수에 대한 예측은 여전히 부족하다.현재 다극 교환 상호작용을 탐색하기 위해 제1원칙 접근방식을 구현한 두 가지 연구가 있다.80년대에 초기 연구가 개발되었습니다.이는 RKKY 메커니즘에 의해 유도되는 결합 상수의 복잡성을 크게 줄일 수 있는 평균 필드 접근법에 기초하고 있기 때문에 다극 교환 해밀토니안은 단지 몇 가지 알려지지 않은 매개 변수로 설명될 수 있으며 실험 ^[23]데이터에 적합함으로써 얻을 수 있다.나중에, 알려지지 않은 매개변수를 추정하기 위한 제1원칙 접근방식이 추가로 개발되었고 몇몇 선택된 화합물(예: 세륨 맘니크타이드)^[24]과 좋은 합의를 얻었다.또 다른 제1원칙적인 접근법도 ^[21]최근에 제안되었다.모든 정적 교환 메커니즘에 의해 유도되는 모든 결합 상수를 일련의 DFT+U 총 에너지 계산에 매핑하고 이산화 우라늄과 일치시킵니다.

레퍼런스