위그너 퀘이프로브성 분포

위그너 퀘이프로빌리티 분포(유진 위그너와 장 안드레 빌레의 뒤를 이어 위그너 함수 또는 위그너-빌 분포라고도 한다)는 퀘이프로빌리티 분포다.1932년^[1] 유진 위너가 고전적 통계역학에 대한 양자교정을 연구하기 위해 도입하였다.슈뢰딩거 방정식에 나타나는 파동 기능을 위상 공간의 확률 분포와 연계시키는 것이 목표였다.

주어진 양자기계파함수 ψ(x)의 모든 공간 자기상관함수에 대한 생성함수다.따라서 1927년 헤르만 베일이 도입한 에르미트 연산자와 실제 위상 공간 함수 사이의 지도에 있는 양자 밀도 행렬을 수학에서의 표현 이론과 관련된 맥락으로 지도화한다^[2](^[3]Weyl 정량화 참조).사실상 위그너다.Weyl 변환 밀도 행렬, 즉 위상 공간에서 연산자의 실현.이후 1948년 장 빌에 의해 신호의 국부적 시간-주파수 에너지, 즉 사실상 분광법으로 2차적(^[4]신호 내) 표현으로 다시 파생되었다.

1949년 독립적으로 이를 도출한 호세 엔리케 모얄은 이를 양자 모멘트 생성 기능으로서,^[5] 따라서 위상공간에서 모든 양자 기대치, 즉 양자역학의 우아한 인코딩의 기초로서 인식하였다(위상공간 공식 참조).전기공학, 지진학, 음악 신호의 시간-주파수 분석, 생물학 및 음성 처리의 분광학, 엔진 설계 등 다양한 분야에서 통계역학, 양자화학, 양자광학, 고전광학, 신호 분석 등에 응용하고 있다.

고전역학과의 관계

고전적인 입자는 확실한 위치와 운동량을 가지고 있으며, 따라서 위상 공간의 한 점에 의해 표현된다.입자의 집합(앙상블)을 감안할 때 위상 공간의 특정 위치에서 입자를 찾을 확률은 확률 분포인 Louville 밀도로 지정된다.이러한 엄격한 해석은 불확도 원리로 인해 양자 입자에 대해 실패한다.그 대신 위의 퀘이프로브빌리티 위너 분포는 유사한 역할을 하지만 기존의 확률 분포의 모든 속성을 만족시키지 못하고, 반대로 고전적 분포에서 사용할 수 없는 경계 특성을 만족시킨다.

예를 들어, 위그너 분포는 고전적 모델이 없고 양자-기계적 간섭의 편리한 지표인 상태에 대해 음의 값을 가질 수 있으며 일반적으로 음의 값을 가질 수 있다.(Wigner 기능이 음성이 아닌 순수 상태의 특성은 아래를 참조하십시오.)위그너 분포를 ħ보다 큰 크기의 필터(예를 들어 위상 공간 가우스시언과 경합하여 위상 공간 가우스시언으로 표현, 이하 후시미 표현을 산출함)를 통해 부드럽게 하면 양의 세미데핀 함수가 나타나게 되는데, 즉, 반종류적인 것으로 강요된 것으로 생각할 수 있다.^[a]

그러한 음의 값을 갖는 지역은 (작은 가우스와 함께 그것들을 교란시킴으로써) "작다"라고 증명할 수 있다: 그것들은 몇 they보다 큰 콤팩트 영역으로 확장될 수 없으며, 따라서 고전적 한계에서 사라진다.이들은 than보다 작은 위상공간 영역 내에서 정확한 위치를 허용하지 않는 불확실성 원리에 의해 보호되며, 따라서 그러한 "부정확률"은 역설적이지 않게 렌더링된다.

정의와 의미

순수 상태의 위그너 분포 W(x,p)는 다음과 같이 정의된다.

여기서 ψ은 파동함수, x와 p는 위치 및 운동량이지만 임의의 결합 변수 쌍(예: 전기장의 실제와 가상의 부분 또는 신호의 주파수와 시간)일 수 있다.ψ이 x("beats")에서 지원이 없는 지역에서도 x에서 지원을 받을 수 있다는 점에 유의한다.

x와 p:의 대칭이다.

${\displaystyle W(x,p)={\frac {1}{\pi \hbar }}\int_{-\inflt }^{-\inflt }^{\\inflt }}\\barphi ^{*(p+q)\varphi(p-q)^{-2ix/\dq,}$

여기서 φ은 ψ의 푸리에 변환에 비례하여 정규화된 모멘텀-공간파 함수다.

3D로.

${\displaystyle W({\vec {r}},{\vec {p}})={\frac {1}{(2\pi )^{3}}}\int \psi ^{*}({\vec {r}}+\hbar {\vec {s}}/2)\psi ({\vec {r}}-\hbar {\vec {s}}/2)e^{i{\vec {p}}\cdot {\vec {s}}}\,d^{3}s.}$

혼합 상태를 포함하는 일반적인 경우 밀도 매트릭스의 Wigner 변환:

${\displaystyle W(x,p)={\frac {1}{\pi \hbar }}\int_{-\infit }^{\\inflt }\langle x+y {\rho}}}}x-y\angle e^{-2ipypypy/\hbar },dy,}}}},dy,}}}}}}}}}}}}}$

여기서 ⟨x ψ⟩ = ψ(x).이 위그너 변환(또는 지도)은 위상공간 함수를 힐버트-우주 연산자에 매핑하는 위상공간 변환의 역방향으로, 위상공간 변환을 위일정량화(Weyl quantization)로 한다.

따라서 위그너 함수는 위상공간에서 양자역학의 초석이 된다.

1949년, José Enrique Moyal은 위그너 함수가 위상 공간에 통합 측정(확률 밀도 함수에 대한 아날로그)을 제공하는 방법(Weyl's transformation을 통해 적절하게 정렬된 연산자 Ⅱ와 관련된 위상 공간 c-숫자 함수 g(x, p)로부터 기대값을 산출하는 방법을 설명했다(Wigner– 참조).Weyl 변환 및 속성 7), 고전적 확률 이론을 환기하는 방식으로.

특히, 사업자의 ĝ 기대값은 해당 사업자의 위그너 변환의 "위상 공간 평균"이다.

${\displaystyle \langle {\G}\angle =\int dx\,dp\,W(x,p)g(x,p)g.}$

수학적 특성

1. W(x, p)는 실제 값 함수다.

2. x 및 p 확률 분포는 여백에 의해 주어진다.

${\displaystyle \int _{-\infty }^{\infty }dp\,W(x,p)=\langle x {\hat {\rho }} x\rangle .}$ If the system can be described by a pure state, one gets ${\displaystyle \int _{-\infty }^{\infty }dp\,W(x,p)= \psi (x) ^{2}.$$}$

${\displaystyle \int _{-\infty }^{\infty }dx\,W(x,p)=\langle p {\hat {\rho }} p\rangle .}$ If the system can be described by a pure state, one has ${\displaystyle \int _{-\infty }^{\infty }dx\,W(x,p)= \varphi (p) ^{2}.$$}$

${\displaystyle \int _{-\ft \}^{-\dx\int _{-\ft }p\,W(x,p)=\operatorname {Tr}({\hat {\rho }}).}$

$일반적$으로 밀도 행렬 ^$$ {\$displaystyle {\hat {\rho }}$의 추적은 1과 같다$$.

3. W(x, p)에는 다음과 같은 반사 대칭이 있다.

• 시간 대칭: ${\displaystyle \psi }$( x${\displaystyle }$)${\displaystyle }$→ ${\displaystyle \psi }$ (${\displaystyle x{}^{}}$) → ${\displaystyle {}^{}}$ W${\displaystyle }$( ${\displaystyle x}$, p${\displaystyle }$)${\displaystyle }$→ ${\displaystyle W}$( ${\displaystyle x}$,${\displaystyle }$- p${\displaystyle }$)${\displaystyle }$. ${\displaystyle \psi (x)\psi (x)^{*}\$Rightarrow W(x$,p)\to W(x,-p$)\$to.$$}$
• 공간 대칭: ${\displaystyle \psi }$( x${\displaystyle }$)${\displaystyle }$→ ${\displaystyle \psi }$(${\displaystyle }$- ${\displaystyle x}$) → ${\displaystyle W}$( ${\displaystyle x}$, ${\displaystyle p}$)${\displaystyle }$→ ${\displaystyle W}$(${\displaystyle }$- ${\displaystyle x}$,${\displaystyle }$- p )${\displaystyle }$.${\displaystyle \psi (x)\to \psi(-x)\rightarrow$W$(x,p)\to W(-x,-p$)\to$.$$}$

4. W(x, p)는 갈릴레이 공변량이다.

${\displaystyle \psi (x)\to \psi (x+y)\Rightarrow W(x,p)\to W(x+y,p)\to W(x+y,p).}$

그것은 로렌츠 공변량이 아니다.

5. 위상 공간의 각 점에 대한 운동 방정식은 힘이 없을 때 고전적이다.

${\displaystyle {\frac {\partial W(x,p)}{\partial t}={\partial t}{\prac {-p}{\partial W(x,p)}{\partial x}}}.}$

사실 조화력이 있는 곳에서도 고전적이다.

6. 상태 중복은 다음과 같이 계산된다.

${\displaystyle \langle \cHB\{2}=2\pi \hbar \int _{-\infit }^{-\infit }dx\int _{-\infit }^{-\infit }dp\,W_{\psi }(x,p)W_{\theta }(x,p).}$

7. 연산자 기대값(평균)은 각 위그너 변환의 위상 공간 평균으로 계산한다.

${\displaystyle g(x,p)\equiv \int _{-\nflass }^{\inflit }dy\langle x-{\frac {y}{2}}\\hat{{G}\좌측 x+{2}}\\오른쪽\rangle e^{ipy/hbar }}}}}}}$

${\displaystyle \langle \psi {\hat {G}} \psi \rangle =\operatorname {Tr} ({\hat {\rho }}{\hat {G}})=\int _{-\infty }^{\infty }dx\int _{-\infty }^{\infty }dp\,W(x,p)g(x,p).}$

8. W(x, p)가 물리적(양) 밀도 매트릭스를 나타내려면 충족해야 한다.

${\displaystyle \int _{-\ft \}^{}dx\,\int _{-\ft }^{\npt }dp\,W(x,p)W_{\theta }(x,p)\geq 0}$

모든 순수한 상태 for⟩에 대하여.

9. Cauchy-Schwarz 불평등 때문에 순수한 상태에서는 다음과 같이 제한된다.

${\displaystyle -{\frac {2}{h}\leq W(x,p)\leq {\frac {2}{h}}.}$

이 바운드는 고전적 한계인 ħ → 0에서 사라진다.이 한계에서 W(x, p)는 좌표 공간 x에서 확률 밀도로 감소하며, 일반적으로 국소성이 높고 운동량에서 Δ-기능을 곱한다: 고전적 한계는 "스파이키"이다.따라서 이 양자-기계적 결합은 불확실성 원리의 반영으로서 위상 공간에서 완벽하게 국부화된 Δ-함수인 위그너 함수를 배제한다.^[6]

10. 위그너 변환은 단순히 그 행렬이 위치 기준으로 표현될 때 밀도 행렬의 항지각의 푸리에 변환일 뿐이다.^[7]

예

${\displaystyle \frac{{}^{}}{\sqrt{}}}$ ${\displaystyle ⟩}$ ${\displaystyle \frac{{\equiv }^{}}{\sqrt{}}m\frac{}{}\mathrm{}}$ ! 0 ${\displaystyle ⟩}$ ${\displaystyle m\rangele \equiv {\frac$ {$a^{\dager$ m$}{\sqrt {m!$$}}} 0\rangele }$은(는) 양자 고조파 오실레이터의 $m{\displaystyle }$ ${\displaystyle m}$ -th$$ Fock 상태임.Groenewold(1946)는 치수 없는 변수에서 관련 Wigner 함수를 발견했다.

${\displaystyle W_{m_{m\rangele }(x,p)={\frac {(-1)^{m}}{\pi }{}e^{-(x^{2}+p^{2})}}L_{m}{\big (}2(p^{2}+x^{2}){{\big )}}}$

여기서 $L{\displaystyle {}_{}}$ ${\displaystyle m_{}}$( ${\displaystyle x}$) ${\displaystyle L_{m}(x)}$은 $m{\displaystyle }$ ${\displaystyle m}$ -th$$ Laguerre 다항식을 나타낸다.

이는 정적 고유 상태 파형 기능에 대한 표현으로 이어질 수 있다.

${\displaystyle u_{m}(x)=\pi ^{-1/4}H_{m}(x)e^{-x^{2}/2},}$

여기서 $H{\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\$는 $m{\displaystyle }$ ${\displaystyle m}$ -th$$ Hermite 다항식이다.위그너 함수의 위그너 함수의 정의로부터, 통합 변수의 변경에 따라,

${\displaystyle W_{m\rangele }(x,p)={\frac {(-1)^{m}{\pi ^{3/2}2^{m}m!2}}e^{-x^{2}-p^{2}}\int_{-\int }^{{-\infit }^{\d\zeta \,e^{-\zeta ^{2}}H_{m}(\zeta -ip+x)H_{m}(\zeta -ip-x).}$

그런 다음 헤르미테와 라구에르 다항식 사이의 일체적 관계에서 그 표현이 따르게 된다.^[8]

위그너 함수의 진화 방정식

위그너 변환은 힐버트 공간의 연산자 ĝ을 위상 공간의 함수 g(x, p)로 변환하는 일반적인 변환이며, 다음이 주어진다.

${\displaystyle g(x,p)=\int _{-\inflit }^{{-\noth/\hbar }\왼쪽\langle x-{\langle x-{{\frac {s}}{{{G}}}\frac {s}}{2}}\{{{2}}\오른쪽\}}}}}$

은둔자 연산자는 실제 기능에 매핑한다.위상공간에서 힐버트공간에 이르는 이 변환의 역행은 Weyl 변환이라고 불린다.

${\displaystyle \langle x {\G}y\rangele =\int_{-\not_{-\frac {dp}{h}{h}e^{ip(x-y)/\hbar }g\왼쪽({\frac {x+y}{2}},p\오른쪽)}$

(미분 기하학의 뚜렷한 Weyl 변환과 혼동되지 않도록 함).

따라서 여기서 논하는 위그너 함수 W(x, p)는 밀도 매트릭스 연산자 ρ̂의 위그너 변환으로 보인다.따라서 밀도 매트릭스 위그너 변환을 가진 연산자의 추적은 위그너 함수와 g(x, p)의 등가 위상 공간 적분 중첩으로 나타난다.

슈뢰딩거 그림의 밀도 행렬의 폰 노이만 진화 방정식의 위그너 변환은 위그너 함수에 대한 모얄의 진화 방정식이다.

여기서 H(x, p)는 해밀턴어, {{⋅, ⋅}}는 모얄어 브래킷이다.고전적 한계인 ħ → 0에서 모얄 브래킷은 포아송 브래킷으로 감소하는 반면, 이 진화 방정식은 고전적 통계 역학의 리우빌 방정식으로 감소한다.

형식적으로, 고전적인 Louville 방정식은 고전적인 해밀턴 방정식의 해법인 위상 공간 입자 궤적 측면에서 해결될 수 있다.이 부분 미분방정식을 푸는 기법은 특성의 방법으로 알려져 있다.이 방법은 양자 시스템으로 전달되며, 여기서 특성의 "트래젝토리"가 이제 위그너 함수의 진화를 결정한다.위그너 함수에 대한 모얄 진화 방정식의 해법은 다음과 같이 공식적으로 표현된다.

$[\displaystyle W(x,p,t)=W{\big (}\star {\big (}x_{-t})(x,p),p_{-t}(x,p){\big )},0{\big )},}$

where ${\displaystyle x_{t}(x,p)}$ and ${\displaystyle p_{t}(x,p)}$ are the characteristic trajectories subject to the quantum Hamilton equations with initial conditions ${\displaystyle x_{t=0}(x,p)=x}$ and ${\displaystyle p_{t=0}(x,p)=p}$$$, 여기서${\displaystyle }$where ${\displaystyle \star$} -제품$$ 구성이 모든 인수 함수에 대해 이해된다.

$\star {\displaystyle }$ ${\displaystyle \star}$ -함수의 구성은$$ 완전히 국소적이지 않기 때문에(Moyal이 관측한 "양자 확률 유체" 확산) 양자 시스템에서 국소 궤적의 잔재는 위그너 분포 함수의 진화에서 거의 식별할 수 없다.^[b]$\star {\displaystyle }$ ${\displaystyle \star }$ - products의$$ 통합적 표현에서, Wigner^[9] 함수의 진화 방정식을 해결하기 위해 그에 의한 연속적인 조작이 위상 공간 경로 적분으로 조정되었다( 참조).모얄 시간 진화의^[13] 이 비 국부적 특성은 하기의 갤러리에 설명되어 있는데, 해밀턴 사람들은 조화 진동자보다 더 복잡한 것이다.고전적 한계에서 위그너 함수의 시간 진화의 궤적 성질은 점점 더 뚜렷해진다.ħ = 0에서 특성의 궤도는 위상 공간에서 입자의 고전적인 궤도로 감소한다.

조화-오일레이터 시간 진화

그러나 양자 고조파 오실레이터의 특별한 경우 진화는 간단하며 고전적인 운동인 오실레이터 주파수가 주어진 주파수로 위상 공간의 경직된 회전과 동일하게 나타난다.이것은 아래 갤러리에 설명되어 있다.이와 같은 동시 진화는 고조파 오실레이터인 광 모드의 양자 상태에서 발생한다.

고전적 한계

위그너 함수는 위상 공간의 고전적 역학 및 양자 역학을 비교함으로써 고전적 한계를 연구할 수 있게 한다.^[15][16]

버나드 콥만과 존 폰 노이만이 1932년에 도입한 고전역학의 운영자적 공식에 대한 위그너 함수 접근법: 위그너 함수의 시간 진화가 접근하는 시간, 한계 0 → 0에서, 고전적 콥만-본 노이만 파동함수의 시간 진화에 대한 양자적 비유로 볼 수 있다고 제안되었다.알 ^[17]입자

위그너 함수의 긍정성

이미 언급한 바와 같이 양자 상태의 위그너 함수는 일반적으로 일부 음의 값을 취한다.실제로 한 변수의 순수 상태의 경우, $모든{\displaystyle }$ x$${\$displaystyle x}$ 및$$ $p{\displaystyle }${\$displaystyle p$}에 ${\displaystyle \mathrm{대해}}$W(${\displaystyle x}$,${\displaystyle p}$)${\displaystyle }$0$${\$displaystyle W(x,p)\geq$ 0$}$이(가)이면 파형 함수의 형식이 있어야 한다$.$

${\displaystyle \cs(x)=e^{-ax^{2}+bx+c}}$

일부 복잡한 숫자의 경우, ()> ${\displaystyle \operatorname {Re} (a)>0}($Hudson의 정리^[18])이$$ 있는 a$,$ b$,b,c}.$${\displaystyle a}$은(는) 복잡할 수 있으므로$$ $\psi {\displaystyle }$ ${\displaystyle \psi }$은(는) 일반적인 의미에서 반드시 가우스파 패킷이 될 필요는$$ 없다는 점에 유의하십시오.따라서 비음성 위그너 함수를 가진 순수 상태는 하이젠베르크 불확도 공식의 의미에서 반드시 최소불확실성 상태일 필요는 없으며, 오히려 정류자 용어 외에 반공칭 용어를 포함하는 슈뢰딩거 불확도 공식에서 동등성을 부여한다.(각각의 분산을 신중하게 정의하여, al.l 순수 상태 위그너 함수는 하이젠베르크의 불평등을 초래한다.)

더 높은 차원에서는 음이 아닌 Wigner 기능을 가진 순수 상태의 특성화가 유사하며, 파동 함수는 반드시 형태를 가져야 한다.

${\displaystyle \psi(x)=e^{-(x,Ax)+b\cdot x+c}}$

$여기$서 ${\displaystyle A}$은(는) 실제 부분이 양의 정의인 대칭 복합 행렬이고, $b{\displaystyle }$ ${\displaystyle b}$은(^[19]는) 복합 벡터, c는 복합 숫자다.그러한 상태의 위그너 함수는 위상 공간에 대한 가우스 분포다.

소토와 클라베리는^[19] 세갈-바르그만 변환을 사용하여 이러한 성격화의 우아한 증거를 제시한다.그 추리는 다음과 같다.$\psi {\displaystyle }$ ${\displaystyle \psi}$의 후시미 Q 함수는 $\psi {\displaystyle }$ ${\displaystyle$$\psi$}의$$세갈-바르그만 변환의 제곱에 가우스 값을 곱한 값으로 계산할 수 있다$$.한편 후시미 Q 함수는 가우스와 위그너 함수의 콘볼루션이다.${\displaystyle \psi }$의 위그너 기능이 위상 공간 어디에서나 음이 아닌 경우$$, 후시미 Q 기능은 위상 공간 어디에서나 엄격히 긍정적일 것이다.$따라서{\displaystyle }$ { ${\displaystyle \psi }$의 Segal-Bargmann 변환 $F{\displaystyle (x}$+ ${\displaystyle i}$ ${\displaystyle p}$) ${\displaystyle F(x+ip)}$은 0이 될 수 없다$$.따라서, 복잡한 분석의 표준 결과에 의해, 우리는

${\displaystyle F(x+ip)=e^{g(x+ip)}}}$

일부 홀모픽 함수 $g{\displaystyle }$ ${\displaystyle g$ 그러나 $F{\displaystyle }$ ${\displaystyle F}$이(가우스 측정에 대해 F ${\displaystyle$ F})가 Segal-Bargmann 공간에 속하려면$$($즉{\displaystyle }$, F ${\displaysty$ F$}$이 정사각형으로 통합되려면$$ $)$ 무한대에서 최대 2차 성장을 이루어야$$ 한다.이를 통해 $g{\displaystyle }$ ${\displaystyle g}$이(가) 실제로 2차 다항식이어야 함을$$ 보여주는 데 기초 복합 분석을 사용할 수 있다.따라서 우리는 위그너 함수가 음성이 아닌 순수 상태의 명시적 형태의 Segal-Bargmann 변환을 얻는다.그러면 우리는 위치파 함수의 요청된 형태를 얻기 위해 Segal-Bargmann 변환을 반전시킬 수 있다.

비음성 위그너 함수를 가진 혼합 상태의 단순한 특성화는 나타나지 않는다.

양자역학의 다른 해석과 관련된 위그너 함수

위그너 quasiprobability 분포 함수는 드 브로글리의 앙상블을 설명하는 또 다른 위상공간 분포 함수의 function-변형으로 간주할 수 있는 것으로 나타났다.Bohm 인과 궤적.^[20]바질 힐리는 준확률 분포가 위상 공간에서 "세포"의 평균 위치와 운동량 측면에서 다시 표현되는 밀도 행렬로 이해될 수 있음을 보여 주었다.Bohm 해석은 그러한 "세포"의 중심들의 역학을 설명할 수 있게 한다.^[21][22]

위그너 함수에 관한 양자 상태 설명과 상호 편견 없는 근거에 관한 양자 상태 재구성 방법 사이에는 밀접한 관계가 있다.^[23]

양자역학 외부 위그너 함수의 사용

• 망원경이나 광통신장치와 같은 광학 시스템의 모델링에서 위그너 기능은 단순한 광선 추적과 시스템의 전파 분석 사이의 간격을 메우기 위해 사용된다.여기서 p/csi는 소각(기밀) 근사치에서 k = k sin θ ≈ k θ으로 대체한다.이러한 맥락에서 위그너 함수는 간섭의 영향을 여전히 포함하면서 위치 x와 각도 θ에서 광선 측면에서 시스템을 설명하는 데 가장 근접한 기능이다.^[24]어느 지점에서 음성이 되면 단순한 광선 추적만으로 시스템을 모델링할 수 없다.즉, 이 함수의 음의 값은 고전적 광신호의 가보르 한계의 증상이며, with과 관련된 빛의 양자특성의 증상은 아니다.
• 신호 분석에서 시간 변동의 전기 신호, 기계적 진동 또는 음파는 위그너 함수로 표현된다.여기서 x는 시간으로 대체되고 p/m³은 각도 주파수 Ω = 2πf로 대체되며, 여기서 f는 정규 주파수다.
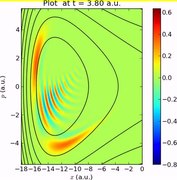
• 초고속 광학에서 짧은 레이저 펄스는 위와 같은 f와 t를 대체하여 위그너 기능을 특징으로 한다.처프(시간에 따른 주파수 변화)와 같은 펄스 결함은 위그너 기능으로 시각화할 수 있다.인접 그림을 참조하십시오.
• 양자 광학에서, x와 p/p는 전기장의 실제 및 가상 구성요소인 X와 P 사분면으로 대체된다(일관된 상태 참조).

위그너 함수의 측정

• 양자단층촬영법
• 주파수 분해 광학 게이트

기타 관련 Quasiprobability 분포

위그너 분포는 공식화된 첫 번째 쿼시프로브성 분포였지만, 공식적으로 동등하고 그것과 변환할 수 있는 더 많은 분포가 뒤따랐다(시간-주파수 분석에서 분포 사이의 변환 참조).좌표계의 경우와 같이, 다양한 특성 때문에, 다음과 같은 여러 가지가 특정 용도에 대해 다양한 장점을 가지고 있다.

• 글라우버 P 표현
• 후시미 Q 표현

그럼에도 불구하고 위그너 분포는 위와 같은 모든 분포 중에서 특권적인 위치를 차지하고 있는데, 이는 위그너 분포가 위에서 설명한 바와 같이 기대치 평가에서 필수 항성생산이 탈락(부품별로 통합되어 효과적인 통합이 이루어짐)되는 유일한 분포이므로, 유사성을 측정하는 준동성 측정으로 시각화할 수 있기 때문이다.o 고전적인 것.

역사 노트

표시된 바와 같이 위그너 함수의 공식은 서로 다른 맥락에서 여러 번 독립적으로 도출되었다.사실, 분명히, 위그너는 양자 이론의 문맥에서도 이전에 하이젠베르크와 Dirac,[25]에 의해 비록 순수하게 공식적으로 소개됐다:이 둘이며, 자신의 부정적인 값 자체가 단지 시스템의 등 전체 양자 설명에 어림한 것이라고 그 의미를 놓쳤다 몰랐다.다다라닷다닷다 라다 라라라. com(불행히도 디락은 나중에 위그너의 처남이 되어 그의 누이 만치와 결혼하게 된다.대칭적으로, 디락은 1940년대 중반 모얄과의 전설적인 18개월간의 서신 대부분에서 모얄의 양자 순간 생성 기능이 사실상 위그너 함수라는 것을 모르고 있었고, 마침내 그것을 그의 주목을 받게 한 것은 모얄이었다.^[26]

참고 항목

각주

참조

추가 읽기

• M. 레반다와 V.플뢰로프(Fleurov), "고전 전자기장 내 전하 입자에 대한 위그너 준분포함수", 물리학연보, 292, 199–231(2001).arXiv:cond-mat/0105137.

외부 링크

• QuTiP에서 Wigner Wigner 기능 구현.
• 양자 광학 갤러리.
• 신호 파일의 Wigner quasiprobability 배포를 위한 Sonogram Visible Speech GPL 라이센스 프리웨어