플러그 유량 원자로 모델

플러그 유량 원자로의 개략도

플러그 유량 원자로 모델(PFR, 때로는 연속관형 원자로, CTR 또는 피스톤 유량 원자로)은 원통형 기하학의 연속적이고 유동적인 시스템에서 화학 반응을 설명하는 데 사용되는 모델이다. PFR 모델은 그러한 설계의 화학 원자로의 거동을 예측하기 위해 사용되며, 원자로의 치수 등 주요 원자로 변수를 추정할 수 있다.

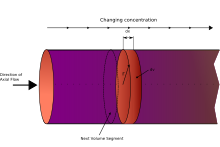
PFR을 통과하는 유체는 각 유체가 원자로의 축방향으로 이동하며 각 유체는 원자로 전후와 다른 구성을 갖는 무한히 얇은 일관 "플러그"의 시리즈로서 원자로를 통과하는 것으로 모델링할 수 있다. 핵심 가정은 플러그가 PFR을 통해 흐를 때 유체가 방사형 방향으로 완벽하게 혼합되지만 축 방향(앞쪽 또는 뒤쪽으로)은 혼합되지 않는다는 것이다. 차동 부피의 각 플러그는 별도의 실체로 간주되며, 사실상 0 부피로 제한되는 극소형 연속 저온 교반 탱크 원자로가 된다. 관형 PFR을 따라 흐를 때 $\tau$ 의 거주 시간 $({\displaystyle \tau }$ )은 원자로 내 위치의 함수다. 따라서 이상적인 PFR에서 거주 시간 분포는 $\tau$ $\tau$ 과(와) 같은 값을 갖는 Dirac 델타 함수가 된다 $\tau$

PFR 모델링

고정 PFR은 적절한 경계 조건을 알면 계산할 수 있는 일반적인 미분방정식에 의해 관리된다.

PFR 모델은 액체, 가스, 슬러리와 같은 많은 액체에 잘 듣는다. 실제 원자로에서는 난류 흐름과 축 확산이 축방향에서 어느 정도의 혼합을 일으키지만, 이러한 영향이 충분히 작아 무시할 수 있을 때 PFR 모델이 적합하다.

PFR 모델의 가장 단순한 경우, 문제를 단순화하기 위해 몇 가지 주요 가정이 이루어져야 하며, 그 중 일부는 아래에 요약되어 있다. 이러한 가정이 모두 필요한 것은 아니지만, 이러한 가정이 제거되면 문제의 복잡성이 증가한다는 점에 유의하십시오. PFR 모델은 온도, 압력 및 흐름의 밀도 변화를 포함하는 반응뿐만 아니라 여러 반응을 모형화하는 데 사용될 수 있다. 이러한 합병증은 뒤에 나오는 것에서는 무시되지만, 산업 공정과 관련이 있는 경우가 많다.

가정:

플러그 흐름
안정 상태
일정한 밀도(일부 액체에 대해서는 타당하지만 중합에 대해서는 20% 오차, 압력 강하, 몰수의 순변동 또는 큰 온도 변화가 없는 경우에만 가스에 유효)
유체의 다량(동종적으로)에서 발생하는 단일 반응.

x와 x + dx 사이의 축 길이 dx 종 i에서 유체 소자 또는 플러그의 차동 부피에 대한 재료 균형은 다음을 제공한다.

[accumulation] = [in] - [out] + [세대] - [ []

일정한 상태에서는 축적량이 0이므로 위의 질량 잔액은 다음과 같이 다시 작성할 수 있다.

1. $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ( x $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ) $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ - $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ( x $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ + $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ) $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ + A $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ = $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ${\displaystyle F_{i}(x)-F_{i}(x+dx)++$ $A_{t}dx\nu _{i}r=0}$ $F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0$ ^[1].

여기서:

x는 원자로관 축방향 위치, m
유체 플러그의 차등 두께 dx
i가 종 i를 가리키는 지수 i.
F_i(x)는 x, mol/s 위치에 있는 종 i의 어금니 유량이다.
D는 튜브 지름, m
A는_t 튜브 횡방향 단면적, m²
ν은 계량계수, 무차원
r은 체적 소스/수치 항(반응 속도), mol/ms이다³.

흐름 선형 속도 u(m/s)와 종 i, C_i(mol/m³)의 농도를 다음과 같이 도입할 수 있다.

{\

A_{t}}={\frac {4{\\dot{v}}{\pi

D

^{2}}:

및

u={\frac {\dot {v}}{A_{t}}}={\frac {4{\dot {v}}}{\pi D^{2}}}

F_{i}=A_{t}uC_{i}\,

=

F_{i}=A_{t}uC_{i}\,

F_{i}=A_{t}uC_{i}\,

F_{i}=A_{t}uC_{i}\,

i

displaystyle F_{i}=

A_{t}uC_{i}\,}

여기서 $˙{\$ 는 ${\dot {v}}$ 체적 유량이다.

위의 내용을 방정식 1에 적용하면 i의 질량 균형이 다음과 같이 된다.

2. $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ [ C $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ ( $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ ) $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ - $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ ( x $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ + $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ x $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ ) $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ + $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ d $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ = $A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,$ ${\$ $A_{t}dx\nu _{i}r=0\,}$ ^[1].

유사 항이 취소되고 방정식 2에 한계 dx → 0이 적용될 때 나는 종에 대한 질량 균형이 된다.

3. $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ = $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ i $u{\frac {dC_{i}}{dx}}=\nu _{i}r$ ${\displaystyle u{{dC_{i}}}{dx}}=\nu _{i}r$ ^[1]

반응률의 온도 의존도 r은 아르헤니우스 방정식을 이용하여 추정할 수 있다. 일반적으로 온도가 올라가면 반응이 일어나는 속도도 증가한다. 거주 시간 $($ tyle $\tau$ $\tau$ 은 별도의 양의 시약이 탱크 내부에서 소비하는 평균 시간이다.

가정:

등온 상태 또는 일정한 온도(k는 일정함)
되돌릴 수 없는 단일 반응(반복_A = -1)
1차 반응(r = k C_A)

위의 가정을 이용하여 방정식 3을 통합한 후, C_A(x)에 대한 해결은 위치 함수로서 종 A의 농도에 대한 명시적인 방정식을 얻게 된다.

4. $C_{A}(x)=C_{A0}e^{-k\tau }\,$ $C_{A}(x)=C_{A0}e^{-k\tau }\,$ ( $C_{A}(x)=C_{A0}e^{-k\tau }\,$ ) $C_{A}(x)=C_{A0}e^{-k\tau }\,$ = $C_{A}(x)=C_{A0}e^{-k\tau }\,$ A $C_{A}(x)=C_{A0}e^{-k\tau }\,$ $C_{A}(x)=C_{A0}e^{-k\tau }\,$ - $C_{A}(x)=C_{A0}e^{-k\tau }\,$ $C_{A}(x)=C_{A0}e^{-k\tau }\,$ $displaystyle C_{A}(x)=$ $C_{A0}e^{-k\tau$ $C_{A}(x)=C_{A0}e^{-k\tau }\,$

여기서 C는_A0 원자로 입구 A종의 농도로서 통합경계조건에서 나타난다.

운영 및 사용

PFR은 "파이프"와 유사한 시스템으로 운송될 때 화합물의 화학적 변환을 모형화하는 데 사용된다. "파이프"는 액체나 가스가 흐르는 다양한 공학적 또는 천연 도관을 나타낼 수 있다. (예: 강, 파이프라인, 두 산 사이의 지역 등)

이상적인 플러그 유량 원자로는 일정한 거주 시간을 갖는다. 시간 $t$ $t$ 에 원자로에 들어가는 모든 액체(플러그)는 t + $t+\tau$ ${\displaystyle$ t $+\tau }$ 에 원자로를 $t$ 빠져나간다 $t+\tau$ 여기서 $\tau$ $\tau$ 은 $\tau$ 원자로 거주 시간이다. 따라서 거주시간 분포 함수는 $\tau$ $\tau$ 에서 디락 델타 함수가 된다 $\tau$ 실제 플러그 유량 원자로는 평균 거주시간 분포를 중심으로 좁은 맥박인 거주시간 분포가 있다.

일반적인 플러그 유량 원자로는 어떤 고체 물질로 채워진 튜브일 수 있다(흔히 촉매). 전형적으로 이러한 유형의 원자로를 포장형 원자로 또는 PBR이라고 부른다. 때때로 튜브는 쉘과 튜브 열 교환기의 튜브가 될 것이다.

플러그 흐름 모델을 적용할 수 없는 경우, 일반적으로 분산 모델을 사용한다.^[2]^[3]

거주시간 분포

원자로의 거주시간 분포(RTD)는 화학원자로에서 발생하는 혼합의 특징이다. 플러그-흐름 원자로에는 축방향 혼합이 없으며, 이러한 누락은 이 등급의 원자로에 의해 전시되는 RTD에 반영된다.^[4]

실제 플러그 유량 원자로는 이상화된 유량 패턴을 만족하지 못하며, 백 믹스 유량 또는 이상 동작으로부터의 플러그 유량 편차는 용기를 통한 유체의 채널링, 용기 내의 유체의 재활용 또는 용기에 정체된 유체 영역 또는 사체 영역의 존재에 기인할 수 있다.^[5] 이상적이지 않은 동작이 있는 실제 플러그 유량 원자로도 모델링되었다.^[6] 화학 원자로로서 선박의 정확한 거동을 예측하기 위해 RTD 또는 자극 반응 기법을 사용한다. 축분산 연구에 가장 널리 사용되는 방법인 추적기 기법은 보통 다음과 같은 형태로 사용된다.^[7]

펄스 입력
스텝 입력
순환입력
임의입력

RTD는 t = 0으로 불리는 불활성 화학 물질, 분자 또는 원자를 원자로에 일정 시간 t = 0으로 주입한 후 시간의 함수로써 유출 흐름에서 추적자 농도 C를 측정함으로써 실험적으로 결정된다.^[4]

혈관을 떠나는 유체의 RTD 곡선을 E-Curve라고 한다. 이 곡선은 그 아래 면적이 통일성이 되도록 평준화된다.

(1)

\int E\partial t=1

출구 스트림의 평균 연령 또는 평균 거주 시간은 다음과 같다.

(2)

\displaystyle \tau =\int tE\partial t=\sum tE\nabla t}

입구에서 하류로 2~3개 이상의 입자 직경이 있는 위치에서 원자로에 추적기를 주입하고 출구로부터 상류로 어느 정도 거리를 측정했을 때, 시스템은 개방 또는 폐쇄 경계 조건의 조합으로 분산 모델에 의해 설명될 수 있다.^[3] 추적기 주입 지점 또는 추적기 측정 지점의 흐름 유형에 불연속성이 없는 그러한 시스템의 경우 개방 시스템의 분산은 다음과 같다.

(3)

{\displaystyle(\sigma _{\te}}^{2}=(\sigma _{t})^{2}/\tau ^{2}=2/P_{e}+8/(P_{e})^{2}}

어디,

(4)

P_{e}=LU/D_{L}

이것은 확산 또는 확산에 의한 대류 이동 속도에 대한 대류 이동 속도의 비율을 나타낸다.

L

L

L

= 특성 길이(m)

D_{L}

D_{L}

{\

스타일 D_

{L

} =

유효

분산 계수

(

m/

D_{L}

s²)

U

U

U

= 빈 단면 기준 표면 속도(m/s)

선박 분산 번호는 다음과 같이 정의된다.

1/P_{e}=D_{L}/LU

한정된 수의 등거리 위치에서 측정된 연속 분포의 분산은 다음과 같다.

(5)

(\sigma _{t}^{2}=\sum t_{i}^{2}C_{i}/\sum C_{i}-\sum [t_{i}C_{i}/\sum C_{i}]^{2}

평균 거주 시간 τ이 주어지는 경우:

(6)

\tau =\sum t_{i}C_{i}/\sum C_{i}}

(7)

{\displaystyle (\displaystyle _{\teta }^{2}=(\displayma _{t})^{2}/\tau ^{2}}:

따라서 ( $(\sigma _{\theta })^{2}$ )²는 C 대 t에 대한 실험 데이터와 $(\sigma _{\theta })^{2}$ ( ) $(\sigma _{\theta })^{2}$ $displaystyle$ 번호 $(1/P_{e})$ ( $(1/P_{e})$ / $(1/P_{e})$ $displaystyle (1/P_{e})$ 는 eq. (3)에서 다음과 같이 평가할 수 있다 $(1/P_{e})$ .

(8)

D_{L}/LU={-1+{\sqrt{1+8(\sigma _{\tea }}^{2}}분 이상 \{1}}}}}}}}}}}}}}}{}}}}}}}}}}}}}}

따라서 축분산 계수 D를_L 추정할 수 있다(L = 포장 높이).^[5]

앞에서 언급했듯이, 분산 번호에 대해 서로 다른 관계를 제공하는 분산 모델에 적용할 수 있는 다른 경계 조건도 있다.^[8]^[9]^[3]

이점

안전 기술 관점에서 PFTR은 다음과 같은 장점을 가지고 있다.

그것은 안정된 상태로 운영된다.
잘 조절할 수 있다.
대형 열전달 구역 설치 가능

걱정

주요 문제점은 어렵고 때로는 중요한 창업과 셧다운 운영에 있다.^[10]

적용들

플러그 유량 원자로는 다음과 같은 용도에 사용된다.

대규모 생산
빠른 반응
동종 또는 이종 반응
연속생산
고온반응

참고 항목

참조 및 출처

^ ^a ^b ^c Schmidt, Lanny D. (1998). The Engineering of Chemical Reactions. New York: Oxford University Press. ISBN 978-0-19-510588-9.
^ Colli, A. N.; Bisang, J. M. (August 2011). "Evaluation of the hydrodynamic behaviour of turbulence promoters in parallel plate electrochemical reactors by means of the dispersion model". Electrochimica Acta. 56 (21): 7312–7318. doi:10.1016/j.electacta.2011.06.047.
^ ^a ^b ^c Colli, A. N.; Bisang, J. M. (September 2015). "Study of the influence of boundary conditions, non ideal stimulus and dynamics of sensors on the evaluation of residence time distributions". Electrochimica Acta. 176: 463–471. doi:10.1016/j.electacta.2015.07.019.
^ ^a ^b Fogler, H. Scott (2004). Elements of Chemical Reaction Engineering (3rd ed.). New Delhi - 110 001: Prentice Hall of India. p. 812. ISBN 978-81-203-2234-9.{{cite book}}: CS1 maint : 위치(링크)
^ ^a ^b Levenspiel, Octave (1998). Chemical Reaction Engineering (Third ed.). John Wiley & Sons. pp. 260–265. ISBN 978-0-471-25424-9.
^ Adeniyi, O. D.; Abdulkareem, A. S.; Odigure, Joseph Obofoni; Aweh, E. A.; Nwokoro, U. T. (October 2003). "Mathematical Modeling and Simulation of a Non-Ideal Plug Flow Reactor in a Saponification Pilot Plant". Assumption University Journal of Technology. 7 (2): 65–74.
^ Coulson, J M; Richardson, J F (1991). "2 - Flow Characteristics of Reactors—Flow Modelling". Chemical Engineering. Vol. 3: Chemical and Biochemical Reactors and Process Control (4th ed.). New Delhi: Asian Books Pvt.Lt. pp. 87–92. ISBN 978-0-08-057154-6.
^ Colli, A. N.; Bisang, J. M. (August 2011). "Evaluation of the hydrodynamic behaviour of turbulence promoters in parallel plate electrochemical reactors by means of the dispersion model". Electrochimica Acta. 56 (21): 7312–7318. doi:10.1016/j.electacta.2011.06.047.
^ Colli, A. N.; Bisang, J. M. (December 2011). "Generalized study of the temporal behaviour in recirculating electrochemical reactor systems". Electrochimica Acta. 58: 406–416. doi:10.1016/j.electacta.2011.09.058.

[Schmidt-1] Schmidt, Lanny D. (1998). The Engineering of Chemical Reactions. New York: Oxford University Press. ISBN 978-0-19-510588-9.

[Colli_and_Bisang,_2011-2] Colli, A. N.; Bisang, J. M. (August 2011). "Evaluation of the hydrodynamic behaviour of turbulence promoters in parallel plate electrochemical reactors by means of the dispersion model". Electrochimica Acta. 56 (21): 7312–7318. doi:10.1016/j.electacta.2011.06.047.

[Colli_and_Bisang,_2015-3] Colli, A. N.; Bisang, J. M. (September 2015). "Study of the influence of boundary conditions, non ideal stimulus and dynamics of sensors on the evaluation of residence time distributions". Electrochimica Acta. 176: 463–471. doi:10.1016/j.electacta.2015.07.019.

[Fogler,_812-4] Fogler, H. Scott (2004). Elements of Chemical Reaction Engineering (3rd ed.). New Delhi - 110 001: Prentice Hall of India. p. 812. ISBN 978-81-203-2234-9.{{cite book}}: CS1 maint : 위치(링크)

[Levenspiel,_260-265-5] Levenspiel, Octave (1998). Chemical Reaction Engineering (Third ed.). John Wiley & Sons. pp. 260–265. ISBN 978-0-471-25424-9.

[Adeniyi_et_al,_2003-6] Adeniyi, O. D.; Abdulkareem, A. S.; Odigure, Joseph Obofoni; Aweh, E. A.; Nwokoro, U. T. (October 2003). "Mathematical Modeling and Simulation of a Non-Ideal Plug Flow Reactor in a Saponification Pilot Plant". Assumption University Journal of Technology. 7 (2): 65–74.

[Coulson_&_Richardson,_87-92-7] Coulson, J M; Richardson, J F (1991). "2 - Flow Characteristics of Reactors—Flow Modelling". Chemical Engineering. Vol. 3: Chemical and Biochemical Reactors and Process Control (4th ed.). New Delhi: Asian Books Pvt.Lt. pp. 87–92. ISBN 978-0-08-057154-6.

[Colli_and_Bisang,_2011a-8] Colli, A. N.; Bisang, J. M. (August 2011). "Evaluation of the hydrodynamic behaviour of turbulence promoters in parallel plate electrochemical reactors by means of the dispersion model". Electrochimica Acta. 56 (21): 7312–7318. doi:10.1016/j.electacta.2011.06.047.

[Colli_and_Bisang,_2011b-9] Colli, A. N.; Bisang, J. M. (December 2011). "Generalized study of the temporal behaviour in recirculating electrochemical reactor systems". Electrochimica Acta. 58: 406–416. doi:10.1016/j.electacta.2011.09.058.

[PFTR-10] 플러그 유량 튜브 원자로 –S2S(발전소와 공정 안전을 위한 관문 방식), 저작권 -2003 by PHP – Nuke

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search