골드바흐 혜성
Goldbach's comet골드바흐 혜성은[1] 이른바 골드바흐 함수인( ) {\의 플롯에 붙여진 이름이다.골드바흐 함수는 골드바흐의 추측과 관련하여 연구된다.함수 ( ) 은 짝수 E> 2 에 대해 E를 두 개의 소수 합으로 표현할 수 있는 여러 가지 방법으로 정의된다.예를 들어, () = 은(는) 세 가지 다른 방법으로 두 프리임의 합으로 표현될 수 있다 = + = + = + [\1719
위의 이미지에서 포인트의 색상은 적색 포인트가 0모드 3, 청색 가 1모드 3, 녹색 포인트가 2모드 3에 해당하는 E/ 스타일 모듈로 3의 값을 기반으로 한다.즉, 빨간색 점은 6의 배수, 파란색 점은 "6의 배수, 더하기 2"의 형태, 녹색 점은 6+4의 배수다.
골드바흐 혜성의 해부학
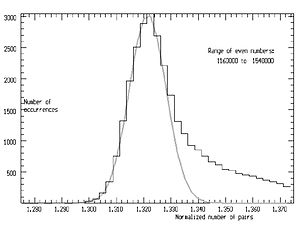
혜성 데이터를 나타내는 명확한 방법은 히스토그램이다.함수 ( ) 은 짝수 E의 1000개 인접 값을 인수하는 국소 평균 g, g로av 나누어 정규화할 수 있다.히스토그램은 중앙 E의 어느 한 쪽에 최대 10%까지 누적될 수 있다.
그런 히스토그램이 오른쪽에 나타난다.일련의 잘 정의된 봉우리들이 뚜렷이 드러난다.이러한 각 피크는 특정 최소 인자를 갖는 / 2 의 값 집합에 의해 형성되는 것으로 식별할 수 있다.주요 피크는 라벨에 표시된 바와 같이 3, 5, 7의 가장 낮은 요인에 해당한다.가장 낮은 요인이 높아지면 피크가 왼쪽으로 이동하고 결국 병합되어 가장 낮은 값의 일차 피크를 제공한다.
사실 피크의 계층 구조가 있다 주요 피크는 보조 피크로 구성되며, / 의 두 번째로 작은 요소들이 연속적으로 나타난다 이 계층 구조는 모든 요소가 소진될 때까지 계속된다.
확대된 섹션은 종속기업 피크의 승계를 보다 상세히 보여준다.
봉우리의 상대적 위치는 하디와 리틀우드가 개발한 형태에서 다음과 같다.[2]
/ 의 인자인 primes p를 모두 인수하는 경우 오른쪽의 인자는 Hardy-Littlewood의 twin prime constant이다.
여기서 제품은 2배 이상의 모든 프라임을 인수한다.
특히 관심 있는 것은 / 의 값만 선택하여 형성된 피크다.(1)식의 제품 계수는 1에 매우 가깝다.봉우리는 가우스 형태(회색으로 표시)에 매우 가깝다.이 E 값 범위의 경우, 피크 위치는 이상적인 }의 0.03% 내에 있다
When histograms are formed for different average values of E, the width of this (primes only) peak is found to be proportional to . However, it is a factor of about 1.85 less than the value that would소수 일치의 완전 무작위 발생 가설에서 예상되다이는 전체 히스토그램에서 분리된 피크를 발생시키는 상관관계가 있기 때문에 예상할 수 있다.
한 프리임이 아니라 E/ 의 전체 범위로 돌아가면, / 의 지정된 최저 인자와 관련된 다른 피크가 가우스인에 의해 장착될 수 있지만, 그 하단 어깨에만 장착될 수 있는 것으로 보인다.부속 봉우리들의 집합체에 의해 형성되는 상부 어깨는 단순한 가우스 형태 위에 놓여 있다.
전체 히스토그램에서 피크의 상대적 높이는 서로 다른 요인을 갖는 다양한 의 E } 모집단을 나타낸다.는 가장 낮은 인자의 산물인\ \,에 대략 반비례한다.따라서 전체 히스토그램에 표시된 피크(3,5)의 높이는 주 피크의 약 1/15이다.높이는 약 20%까지 달라질 수 있다. 정확한 값은 피크가 구성 요소에서 구성되는 방식과 다양한 너비의 복잡한 함수다.
소수 E가 0개의 프라임 쌍을 가지고 있을 가능성에 대해 추측하고, 이러한 가우스 형태를 확률로 받아들이고, 0-페어 포인트로 추론하는 것이 합법적이라고 가정하는 것은 흥미롭다.이렇게 하면 여기서 고려한 범위에서 한 E에 대해 0 쌍의 확률이 순서 10이−3700 된다.피크 폭의 축소를 고려한, 모든 E에서 무한대에 걸친 통합 확률은 그리 크지 않다.골드바흐 추측을 위반하기 위한 어떤 검색도 이러한 가능성이 합리적으로 예상될 수 있다.
참조
- ^ 플리겔, 헨리 F.; 로버슨, 더글러스 S.; "골드바흐 혜성: 골드바흐의 추측과 관련된 숫자"; 레크리에이션 수학 저널 v21(1) 1-7, 1989.
- ^ G. H. Hardy와 J. E. Littlewood, "partitio numumorum의 일부 문제; III: 프리임의 합으로 숫자의 표현에 관한 것", Acta Mathematica, vol. 44, 페이지 1-70, 1922.


 (는) 세 가지 다른 방법으로 두 프리임의 합으로 표현될 수 있다
(는) 세 가지 다른 방법으로 두 프리임의 합으로 표현될 수 있다
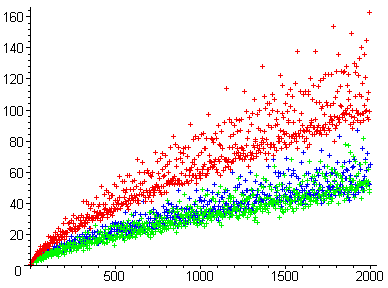
 3의 값을 기반으로 한다.즉, 빨간색 점은 6의 배수, 파란색 점은 "6의 배수, 더하기 2"의 형태, 녹색 점은 6+4의 배수다.
3의 값을 기반으로 한다.즉, 빨간색 점은 6의 배수, 파란색 점은 "6의 배수, 더하기 2"의 형태, 녹색 점은 6+4의 배수다.