오류 임계값(진화)

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "오류 임계값" 진화 – 뉴스 · 신문 · 책 · 학자 · JSTOR (2012년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

진화 생물학 및 인구 유전학에서 오류 임계값(또는 임계 돌연변이 비율)은 돌연변이가 분자의 다음 세대에서 정보를 파괴하기 전에 자기복제 분자가 가질 수 있는 염기쌍의 수에 대한 제한이다.에러 문턱은 "아이겐의 역설"을 이해하는 데 중요하다.

오류 문턱은 DNA가 출현하기 전, 특히 초기의 생명체(abiogenesis)의 기원(abiogenesis)에 있는 개념이다.최초의 자가복제 분자는 작은 리보핵산 같은 RNA 분자였을 것으로 추측된다.이들 분자는 염기쌍이나 "자릿수"의 끈으로 구성되며, 그 순서는 분자가 환경과 상호 작용하는 방법을 지시하는 코드다.모든 복제는 돌연변이 오류가 발생할 수 있다.복제 과정 동안, 각 자릿수는 분자가 환경과 상호작용하는 방식을 변화시키는 몇몇 다른 숫자로 대체될 확률을 가지고 있으며, 그러한 환경에서는 그 적합성 또는 재생산 능력을 증가시키거나 감소시킬 수 있다.

피트니스 풍경

Manfred Eigen은 1971년 논문(Eigen 1971)에서 이 돌연변이 과정은 분자가 가질 수 있는 자릿수에 제한을 둔다고 지적했다.분자가 이 임계 크기를 초과하면 돌연변이의 효과는 압도적으로 커지며, 폭주하는 돌연변이 과정은 분자의 다음 세대에서 정보를 파괴할 것이다.오차 한계치는 분자에 대한 "피트니스 풍경"에 의해서도 제어된다.피트니스 풍경은 키(=피트니스)와 거리(=변종 횟수)의 두 가지 개념으로 특징지어진다.비슷한 분자는 서로 '가까이' 있고, 다른 분자보다 더 적합하고 번식 가능성이 높은 분자는 풍경 속에서 '높이' 있다.

특정 시퀀스와 그 이웃들이 높은 건강성을 지닐 경우, 그들은 기형종을 형성할 것이고, 적합된 이웃이 거의 없는 적합 시퀀스보다 더 긴 시퀀스 길이를 지원할 수 있을 것이다.또한 Wilke(Wilke 2005)는 유도 돌연변이가 0의 적합성을 산출하고 분자의 번식을 금지하는 치명적인 돌연변이가 있는 경관의 일부에는 오차 한계치 개념이 적용되지 않는다는 점에 주목했다.

아이겐의 역설

아이겐의 역설은 생명의 기원에 대한 연구에서 가장 난해한 퍼즐 중의 하나이다.위에서 설명한 오류 한계치 개념은 분자의 크기를 수백 자리까지 제한한다고 생각되지만, 지구상의 거의 모든 생명체는 그들의 유전 정보를 인코딩하기 위해 훨씬 더 긴 분자를 필요로 한다.이 문제는 살아있는 세포에서 돌연변이를 복구하는 효소에 의해 처리되어 인코딩 분자가 수백만 개의 염기쌍의 크기에 도달할 수 있게 한다.물론 이 큰 분자들은 자신을 회복시키는 바로 그 효소를 인코딩해야 하며, 여기에 맨프레드 아이겐이 1971년 논문에서 처음 제시한 아이겐의 역설(아이겐 1971)이 있다.^[1]간단히 말해 아이겐의 역설은 다음과 같다.

• 오류 수정 효소가 없다면, 복제 분자의 최대 크기는 약 100개의 염기쌍이다.
• 복제 분자가 오류 수정 효소를 인코딩하려면 100 염기보다 실질적으로 커야 한다.

이것은 훨씬 더 어려운 해결책이 있는 일종의 역설이다.큰 게놈과 오류 수정 효소 중 어느 것이 먼저인가?이러한 모순에 대한 많은 해결책이 제안되었다.

• 확률적 교정기 모델(Szathmary & Maynard Smith, 1995).이 제안된 해결책에서, 두 가지 다른 유형의 원시적인 분자들은 아마도 캡슐이나 "세포 벽"에 의해 어떤 식으로든 서로 연관되어 있다.만약 그들의 생식 성공이 각 세포에 동일한 수를 가지면서 향상되고, 다양한 종류의 분자가 "아이들" 사이에 무작위로 분포되는 분열에 의해 생식이 일어난다면, 비록 그 분자 중 하나가 선택적 고증을 가질 수 있을지라도, 선택 과정은 세포에서 그러한 동등한 표현을 촉진할 것이다.상대편보다 뒤떨어지다
• 완화된 오류 임계값(Kun 등, 2005년) - 실제 이등분자에 대한 연구는 돌연변이 비율이 복제당 기본 쌍당 0.001의 순서로 처음 예상보다 상당히 낮을 수 있다는 것을 보여준다.이를 통해 기본 오류 보정 효소를 포함하기에 충분한 7~8천 염기쌍의 순서 길이가 허용될 수 있다.

간단한 수학적 모형

A, B, C가 값 0과 1을 차지할 수 있는 3자리 분자[A,B,C]를 고려한다.8개의 순서([000], [001], [010], [011], [100], [101], [110], [111])가 있다.[000] 분자가 가장 적합하다고 가정해 봅시다. 각 복제 시마다 평균$${\$displaystyle$ a$}$의 복사본이 생성되는데 서 > 1 ${\displaystyle a>1$이 분자는 "마스터 시퀀스"라고 불린다.나머지 7개의 순서는 덜 적합하다. 각각 복제당 1개의 복사본만 생산한다.세 자리 각각에 대한 복제는 μ의 돌연변이 비율로 이루어진다.즉, 시퀀스의 자릿수를 복제할 때마다 오류가 발생할$$ 확률 $\mu {\displaystyle }$ ${\displaystyle \mu }$이(가) 있으며, 0은 1로 대체되거나 그 반대로 변경된다.이중 돌연변이와 분자의 죽음(인구는 무한히 증가할 것이다)은 무시하고, 8개의 분자를 마스터 시퀀스로부터의 해밍 거리에 따라 세 부류로 나누자.

해밍 거리를 두다	시퀀스
0	[000]
1	[001] [010] [100]
2	[110] [101] [011]
3	[111]

거리 d에 대한 시퀀스 수는 L=3에 대한$$ 이항계수$({\displaystyle \genfrac{}{}{0ex}{}{L}{}}$ d${\displaystyle }$) ${\${\$tbinom {L}{d}}}$에 불과하며, 각 시퀀스를 L=3차원 입방체의 정점으로 시각화할 수 있으며, 해밍 거리가 0 또는 ±1인 돌연변이 경로를 지정하는 큐브의 각 가장자리로 지정할 수 있다.예를 들어, [001] 분자의 돌연변이의 3분의 1이 [000]개의 분자를 생성하는 반면, 나머지 3분의 2는 등급2의 분자를 생성한다고 볼 수 있다[011]와 [101].이제 부모 $모집단{\displaystyle {}_{}}$ n ${\displaystyle j_{}}$ ${\$$displaystyle n'_{i}$의 하위$$ 모집단 $n{\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$$displaystyle n_{j}$에 대한 식을 쓸 수 있다$.$

${\displaystyle n'_{i}=\sum _{j=0}^{3}w_{ij}n_{j}}}}}$

진원종 모델에 따라 자연 선택과 돌연변이를 통합한 매트릭스 'w'는 다음과 같이 제공된다.

${\displaystyle \mathbf {w} ={\begin{bmatrix}a\cdot Q&3a\cdot \mu &Q&0&0\\\0&2\mu &0&0&3\mu &Q>end{bmatrix}}}}}}}}}$

여기서 $Q{\displaystyle }$=${\displaystyle }$( ${\displaystyle 1\mu {}^{}}$) L ${\$ Q$=(1-\mu )^{L}}$는 전체 분자가 성공적으로 복제될 확률이다$$.w 행렬의 고유 벡터는 각 등급에 대한 평형 모집단 수를 산출한다.예를 들어 돌연변이율 μ가 0이면 Q=1이 되고 평형농도는${\displaystyle }$[${\displaystyle \mathrm{n}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}}$n ${\displaystyle {3\mathrm{}}_{}}$ ${\displaystyle {}_{}}$= [${\displaystyle }$1${\displaystyle ,}$ ${\displaystyle 0,}$ ${\displaystyle 0}$, 0${\displaystyle ]}$ ${\displaystyle [n_{0},n_{1},n_{2},n_{3}}}}}=[1,0,$0,$0,$0,0$,0$]이 된다$.$가장 적합한 순서가 살아남는 유일한 순서가 될 거야Q=0.95의 복제 충실도와 a=1.05의 유전적 장점을 가지고 있다면 평형 농도는 대략${\displaystyle }$[${\displaystyle 0.33,0.38,}$ ${\displaystyle 0.24,}$ ${\displaystyle 0.06}$ ${\displaystyle ]}$ $[\displaystyle [0.33,0.38,0.24,0.06]}$이 될 것이다$.$ 마스터 시퀀스가 우세하지 않음을 알 수 있다. 그럼에도 불구하고 해밍 거리가 낮은 시퀀스는 대다수를 차지한다.Q의 복제 충실도가 0에 근접하면 평형 농도는 대략${\displaystyle }$[ ${\displaystyle 0.125,0.375,}$ ${\displaystyle 0.375}$, 0.375${\displaystyle ,0.125}$ ${\displaystyle ]}$ ${\displaystyle [0.125,$0$.375,$ 0.$375,0.$375$,0$.125$]\}$이 될 것이다.이것은 8개의 시퀀스 각각에 동일한 개수를 가진 모집단이다.(모든 시퀀스에서 모집단이 완벽하게 같다면 [1,3,3,1]/8의 모집단이 있을 것이다.)

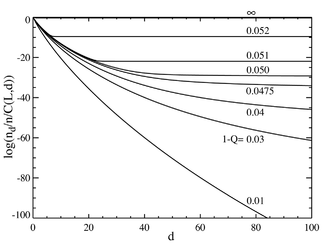
만약 우리가 지금 L=100이라고 하는 염기쌍의 수가 큰 경우로 간다면, 우리는 위상전환을 닮은 행동을 얻게 된다.왼쪽 그림에는 이항계수$($ k$displaystyle {\tbinom{100}{k}}}}$로 나눈 일련의 평형농도가 표시된다$.$ (이 곱셈은 해당 거리에서 개별 시퀀스에 대한 모집단을 보여 주며, 동일한 분포에 대해 평형선을 산출한다.)마스터 시퀀스의 선택적 우위는 a=1.05로 설정된다.수평축은 해밍 거리 d이다.다양한 곡선은 다양한 총 돌연변이 비율$({\displaystyle 1}$- Q$){\displaystyle (1-Q)}$에 대한 것으로$,$ 총 돌연변이 비율의 낮은 값의 경우, 모집단은 마스터 시퀀스 주변에 모여 있는 메아시스형으로 구성된다.약 1-Q=0.05의 총 돌연변이 비율 이상에서는 분포가 빠르게 퍼져 모든 시퀀스를 균등하게 채운다.오른쪽 아래의 그림은 총 돌연변이 비율의 함수로서 마스터 시퀀스의 부분 모집단을 보여준다.다시 보면, 약 1-Q=0.05의 임계 돌연변이 비율 이하에서는 마스터 시퀀스가 대부분의 모집단을 포함하고 있는 반면, 이 비율 이상에서는 전체 모집단의 $약$ 2${\displaystyle {}^{}}$- ${\displaystyle L^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {10}^{}}$- ${\displaystyle {30}^{}}$ $[\$ 스타일 $2^{-L}\$약$10^{-30}}$만을 포함하고 있는 것으로 보인다.

0.05보다 조금 큰 1Q의 값에서 급격한 전환이 있음을 알 수 있다.이 값을 초과하는 돌연변이 비율의 경우 마스터 시퀀스의 모집단은 사실상 0으로 떨어진다.이 값 이상으로 지배한다.

L이 무한대에 접근하는 한계에서, 시스템은 사실상 Q: ${\displaystyle \mathrm{Q}}$ ${\displaystyle c_{}}$= ${\displaystyle 1}$/ a${\displaystyle }$. ${\displaystyle Q_{c}=1/a.}$의 임계값으로 위상전환을 한다$.$ 전체 돌연변이율(1-Q)을 일종의 "온도"로 생각할 수 있는데, 이는 $1{\displaystyle \mathrm{}}$- ${\displaystyle {}_{}}$의 임계 온도보다 분자 시퀀스의 충실도를 "융"하는 것이다.${\displaystyle c_{}}$ ${\$ 충실한 복제가 일어나려면 정보가 게놈에 "동결"되어야 한다.

참고 항목

• 에러 대재앙
• 소멸 소용돌이
• 유전 엔트로피
• 유전적 침식
• 뮬러 래칫

참조

• Eigen, M. (1971). "Selforganization of matter and evolution of biological Macromolecules". Naturwissenschaften. 58 (10): 465–523. Bibcode:1971NW.....58..465E. doi:10.1007/BF00623322. PMID 4942363. S2CID 38296619.
• "Quasispecies theory in the context of population genetics - Claus O. Wilke" (PDF). Retrieved October 12, 2005.
• Campos, P. R. A.; Fontanari, J. F. (1999). "Finite-size scaling of the error threshold transition in finite populations" (PDF). J. Phys. A: Math. Gen. 32: L1–L7. arXiv:cond-mat/9809209. Bibcode:1999JPhA...32L...1C. doi:10.1088/0305-4470/32/1/001. S2CID 16500591.
• Holmes, Edward C. (2005). "On being the right size". Nature Genetics. 37 (9): 923–924. doi:10.1038/ng0905-923. PMC 7097767. PMID 16132047.
• Eörs Szathmáry; John Maynard Smith (1995). "The major evolutionary transitions". Nature. 374 (6519): 227–232. Bibcode:1995Natur.374..227S. doi:10.1038/374227a0. PMID 7885442. S2CID 4315120.
• Luis Villarreal; Guenther Witzany (2013). "Rethinking quasispecies theory: From fittest type to cooperative consortia". World Journal of Biological Chemistry. 4 (4): 79–90. doi:10.4331/wjbc.v4.i4.79. PMC 3856310. PMID 24340131.
• Ádám Kun; Mauro Santos; Eörs Szathmáry (2005). "Real ribozymes suggest a relaxed error threshold". Nature Genetics. 37 (9): 1008–1011. doi:10.1038/ng1621. PMID 16127452. S2CID 30582475.