논리 게이트
Logic gate

논리 게이트는 단일 이진 출력을 생성하는 하나 이상의 이진 입력에 대해 수행되는 논리 연산인 부울 함수를 수행하는 이상화된 또는 물리적 장치입니다.
문맥에 따라, 용어는, 예를 들어, 제로 라이즈 타임 및 무제한 팬-아웃을 갖는 이상적인 논리 게이트를 나타낼 수도 있고, 또는 비이상적인 물리 디바이스를[1] 나타낼 수도 있습니다(비교를 위해 이상적인 및 실제 op-amp 참조).
실제 세계에서 논리 게이트를 만드는 주요 방법은 전자 스위치 역할을 하는 다이오드 또는 트랜지스터를 사용합니다.오늘날 대부분의 논리 게이트는 MOSFET(금속-산화물-반도체 전계 효과 트랜지스터)로 만들어집니다.[2]진공관, 릴레이 로직, 유체 로직, 공압 로직, 광학, 분자 또는 기계적 요소를 사용하여 구성할 수도 있습니다.
증폭을 통해 논리 게이트는 부울 함수를 구성할 수 있는 것과 동일한 방식으로 캐스케이드할 수 있으므로 모든 부울 논리의 물리적 모델을 구성할 수 있습니다. 따라서 부울 논리로 설명할 수 있는 모든 알고리즘과 수학을 구성할 수 있습니다.
논리 회로에는 멀티플렉서, 레지스터, 산술 논리 장치(ALU) 및 컴퓨터 메모리와 같은 장치가 포함되며, 이 장치는 1억 개 이상의 논리 게이트를 포함할 수도 있습니다.
복합 논리 게이트 AOI(And-OR-Invert) 및 OAI(Or-AND-Invert)는 MOSFET을 사용한 구성이 개별 게이트의 합계보다 간단하고 효율적이기 때문에 회로 설계에 종종 사용됩니다.[3]
가역 논리에서는 토폴리 또는 프레드킨 게이트가 사용됩니다.
전자 게이트
기능적으로 완전한 논리 시스템은 릴레이, 밸브(진공 튜브) 또는 트랜지스터로 구성될 수 있습니다.논리 게이트의 가장 단순한 제품군은 바이폴라 트랜지스터를 사용하며, 저항-트랜지스터 논리(RTL)라고 불립니다.이득 요소가 없는 단순 다이오드 논리 게이트와 달리 RTL 게이트는 더 복잡한 논리 기능을 생성하기 위해 무한정 캐스케이드될 수 있습니다.RTL 게이트는 초기 집적 회로에서 사용되었습니다.더 빠른 속도와 더 나은 밀도를 위해, RTL에 사용되는 저항기를 다이오드로 대체하여 다이오드-트랜지스터 논리(DTL)를 만들었습니다.트랜지스터-트랜지스터 로직(TTL)은 그 후 DTL을 대체하였습니다.집적 회로가 복잡해짐에 따라 바이폴라 트랜지스터는 더 작은 전계 효과 트랜지스터(MOSFET)로 대체되었습니다(PMOS 및 NMOS 참조).전력 소비를 더욱 줄이기 위해, 디지털 시스템의 대부분의 현대 칩 구현은 이제 CMOS 로직을 사용합니다.CMOS는 낮은 전력 소산과 함께 빠른 속도를 달성하기 위해 상보적(n채널 및 p채널 모두) MOSFET 장치를 사용합니다.
소규모 논리의 경우, 설계자들은 이제 Texas Instruments의 TTL 7400 시리즈, RCA의 CMOS 4000 시리즈, 그리고 그들의 최근 후손과 같은 장치 계열의 조립식 논리 게이트를 사용합니다.점점 더 이러한 고정 기능 로직 게이트는 설계자가 여러 개의 혼합 로직 게이트를 하나의 집적 회로로 패키징할 수 있도록 하는 프로그래머블 로직 디바이스로 대체되고 있습니다.FPGA와 같은 프로그래밍 가능한 논리 장치의 현장 프로그래밍 가능 특성은 하드웨어의 '하드' 속성을 감소시켰습니다. 이제 하드웨어 시스템의 일부 구성 요소를 재프로그래밍함으로써 하드웨어 시스템의 논리 설계를 변경할 수 있으므로 논리 시스템의 하드웨어 구현의 특징이나 기능을 변경할 수 있습니다.다른 종류의 논리 게이트는 다음과 같습니다.[4]
| 논리계열 | 약칭 | 묘사 |
|---|---|---|
| 다이오드 논리 | DL | |
| 터널 다이오드 로직 | TDL | 다이오드 로직과 동일하지만 더 빠른 속도로 수행할 수 있습니다.[failed verification] |
| 네온논리 | NL | 네온 전구 또는 3요소 네온 트리거 튜브를 사용하여 논리를 수행합니다. |
| 코어 다이오드 로직 | CDL | 반도체 다이오드와 소형 페라이트 토로이달 코어에 의해 수행되어 적당한 속도와 적당한 전력 레벨을 제공합니다. |
| 4계층 디바이스 로직 | 4LDL | 사이리스터 및 SCR을 사용하여 고전류 및 고전압이 필요한 경우 로직 작동을 수행합니다. |
| 직접-커플드 트랜지스터 로직 | DCTL | 포화 상태와 차단 상태 사이의 트랜지스터 전환을 사용하여 논리를 수행합니다.트랜지스터들은 신중하게 조절된 파라미터가 필요합니다.다른 구성 요소가 거의 필요하지 않기 때문에 경제적이지만 사용되는 전압 레벨이 낮기 때문에 노이즈에 취약한 경향이 있습니다.종종 현대 TTL 논리의 아버지로 여겨집니다. |
| 금속-산화물-반도체 로직 | 모스 | 대부분의 최신 논리 게이트의 기본인 MOSFET(금속-산화물-반도체 전계 효과 트랜지스터)를 사용합니다.MOS 로직 제품군은 PMOS 로직, NMOS 로직, CMOS(Complementary MOS) 및 BiCMOS(Bipolar CMOS)를 포함합니다. |
| 전류 모드 논리 | CML | 트랜지스터를 사용하여 논리를 수행하지만, 포화를 방지하고 매우 빠른 스위칭을 가능하게 하기 위해 정전류 소스에서 바이어싱을 수행합니다.상당히 낮은 논리 수준에도 불구하고 높은 소음 내성을 가지고 있습니다. |
| 양자점 셀룰러 오토마타 | QCA | 이진 논리 비트를 합성하기 위해 터널링 가능한 q비트를 사용합니다.양자점 내의 두 전자 사이의 정전기적 반발력은 적합하게 구동된 편광 아래의 전자 구성(고수준 논리 상태 1 또는 저수준 논리 상태 0을 정의하는)을 할당합니다.이것은 무트랜지스터, 무전류, 무접합 이진 논리 합성 기법으로 매우 빠른 연산 속도를 가질 수 있습니다. |
전자 논리 게이트는 릴레이 및 스위치와 상당한 차이가 있습니다.훨씬 빠르고 전력을 훨씬 적게 소비하며 크기도 훨씬 작습니다(대부분의 경우 100만 배 이상).또한 근본적인 구조적 차이가 있습니다.스위치 회로는 입력과 출력 사이에 전류가 (어느 방향으로든) 흐를 수 있는 연속적인 금속 경로를 생성합니다.그러나, 반도체 로직 게이트는 고이득 전압 증폭기로서 기능하는데, 고이득 전압 증폭기는 입력에서 작은 전류를 싱크하고 출력에서 낮은 임피던스 전압을 생성합니다.반도체 로직 게이트의 출력과 입력 사이에는 전류가 흐를 수 없습니다.
7400 및 4000 패밀리와 같은 표준화된 집적 회로 로직 패밀리의 또 다른 중요한 장점은 캐스케이드(cascaded)가 가능하다는 것입니다.이는 하나의 게이트의 출력을 하나 또는 여러 개의 다른 게이트의 입력에 연결할 수 있음을 의미합니다.각 집적 회로의 한계가 고려된다면 게이트 내부 작업에 대해 설계자의 큰 우려 없이 다양한 복잡도의 시스템을 구축할 수 있습니다.
한 게이트의 출력은 다른 게이트에 대한 유한한 수의 입력만을 구동할 수 있으며, 이를 '팬아웃 한계'라고 합니다.또한, 게이트의 입력의 변화로부터 그에 상응하는 출력의 변화에 이르기까지 항상 '전파 지연'이라고 불리는 지연이 존재합니다.게이트들이 계단식일 때, 총 전파 지연은 대략 개별 지연들의 합이고, 이것은 고속 동기 회로에서 문제가 될 수 있는 효과입니다.많은 입력이 출력에 연결되어 있을 때 모든 입력과 배선의 용량이 분산되어 있고 각 출력에서 제공할 수 있는 전류의 양이 한정되어 있기 때문에 추가적인 지연이 발생할 수 있습니다.
역사와 발전
이진법 체계는 고대 이칭의 이진법에 영향을 받아 고트프리트 빌헬름 라이프니츠(1705년 출판)에 의해 정교화되었습니다.[5][6]라이프니츠는 이진법을 사용하여 산술과 논리의 원리를 결합했다고 밝혔습니다.
찰스 샌더스 피어스는 1886년 편지에서 어떻게 논리 연산이 전기 스위칭 회로에 의해 수행될 수 있는지 설명했습니다.[7]초기 전기기계 컴퓨터는 진공관(열이온 밸브)이나 트랜지스터(이후 전자 컴퓨터가 구축된)의 혁신보다는 스위치와 릴레이 로직으로 만들어졌습니다.루트비히 비트겐슈타인(Ludwig Wittgenstein)은 Tractatus Logico-Philosophicus(1921)의 명제 5.101로 16행 진리표의 버전을 소개했습니다.우연 회로의 발명가인 발터 보테는 1924년에 최초의 현대 전자와 게이트로 1954년 노벨 물리학상의 일부를 받았습니다.콘라드 쥐세는 1935년부터 1938년까지 자신의 컴퓨터 Z1을 위한 전자기계 논리 게이트를 설계하고 제작했습니다.
1934년부터 1936년까지 NEC 엔지니어 나카시마 아키라, 클로드 섀넌, 빅터 셰스타코프는 독립적으로 발견한 2-값 부울 대수가 스위칭 회로의 동작을 설명할 수 있다는 것을 보여주는 일련의 논문에서 스위칭 회로 이론을 소개했습니다.[8][9][10][11]이러한 전기 스위치의 특성을 사용하여 로직을 구현하는 것은 모든 전자 디지털 컴퓨터의 기본 개념입니다.스위칭 회로 이론은 제2차 세계 대전 중과 전후에 전기 공학계에 널리 알려졌기 때문에 디지털 회로 설계의 기초가 되었고, 이론적 엄격성은 이전에 우세했던 특별한 방법을 대체했습니다.[11]
벨 연구소 엔지니어 모하메드 M은 PMOS와 NMOS 형태의 MOS(Metal-Oxide-Semiconductor) 장치를 시연했습니다. 1960년의 아탈라와 다원 칸.[12]두 가지 유형은 이후 1963년 Fairchild Semiconductor에서 Chi-Tang Sah와 Frank Wanlass에 의해 상호보완적 MOS(CMOS) 로직으로 결합 및 채택되었습니다.[13]
분자 논리 게이트에서 활발한 연구가 이루어지고 있습니다.
기호
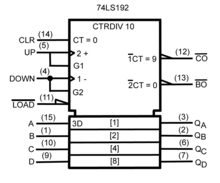
일반적으로 ANSI/IEEE 규격 91-1984 및 그 보충판 ANSI/IEEE 규격 91a-1991에 정의된 기본 논리 게이트에 대한 두 세트의 기호가 있습니다.전통적인 도식에 기초한 "독특한 모양" 세트는 단순한 도면에 사용되며 1950년대와 1960년대의 미국 군사 표준 MIL-STD-806에서 유래했습니다.[14]비공식적으로 "군사"라고 표현되기도 하며, 이는 그 기원을 반영합니다.나중에 IEEE 및 IEC에 의해 개선된 ANSI Y32.14 및 기타 초기 산업 표준에 기초한 "직사각 형상" 세트는 모든 유형의 게이트에 대해 직사각형 윤곽을 가지고 있으며 전통적인 기호로 가능한 것보다 훨씬 더 넓은 범위의 장치를 표현할 수 있습니다.[15]IEC 표준인 IEC 60617-12는 유럽의 경우 EN 60617-12:1999, 영국의 경우 BS EN 60617-12:1999, 독일의 경우 DIN EN 60617-12:1998과 같은 다른 표준에 의해 채택되었습니다.
IEEE 규격 91-1984 및 IEC 617-12의 상호 목표는 디지털 회로의 복잡한 논리 기능을 도식화된 기호로 기술하는 균일한 방법을 제공하는 것이었습니다.이러한 기능은 단순한 AND 및 OR 게이트보다 더 복잡했습니다.마이크로프로세서와 같은 대규모 회로에 대한 4비트 카운터와 같은 중간 규모의 회로가 될 수 있습니다.
IEC 617-12 및 번호가 변경된 후속 IEC 60617-12는 "독특한 형상" 기호를 명시적으로 표시하지 않지만, 이를 금지하지는 않습니다.[15]그러나 ANSI/IEEE 규격 91(및 91a)에 나와 있는 것은 다음과 같습니다. "IEC 간행물 617에 따르면 독특한 모양의 기호는 선호되지 않지만, 그 표준과 모순되는 것으로 간주되지는 않습니다." IEC 60617-12는 이에 상응하여 다음과 같은 내용을 포함하고 있습니다(섹션 2.1). "비선호적이지만, 다른 기호의 사용은 인정합니다.d 기호[기본 관문 목록]을 대신하는 독특한 모양인 공식 국가 표준에 따르면 이 표준과 모순되는 것으로 간주되어서는 안 됩니다.복잡한 기호(예: 내장 기호로 사용)를 형성하기 위해 이러한 다른 기호를 조합하여 사용하는 것은 권장되지 않습니다."이 절충안은 IEEE와 IEC 표준이 상호 준수될 수 있도록 하기 위해 각 IEEE 및 IEC 작업 그룹 간에 이루어졌습니다.
1980년대에 도식화는 게이트 어레이로 알려진 회로 기판과 맞춤형 IC를 모두 설계하는 주요 방법이었습니다.오늘날 사용자 지정 IC 및 필드 프로그래밍 가능 게이트 어레이는 일반적으로 Verilog 또는 VHDL과 같은 HDL(Hardware Description Languages)로 설계됩니다.
| 유형 | 독특한 모양 (IEEE 규격 91/91a-1991) | 사각형 (IEEE 규격 91/91a-1991) (IEC 60617-12:1997) | A와 B 사이의 부울 대수 | 진리표 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 단일 입력 게이트 | ||||||||||||||||||||||
| 버퍼 |
| |||||||||||||||||||||
| 것은 아니다. (inverter) | ¯ {A \ A} |
| ||||||||||||||||||||
| 전자공학에서는 NOT 게이트를 인버터라고 더 흔히 부릅니다.기호의 원을 버블(bubble)이라고 하며, 외부 논리 상태와 내부 논리 상태(1 ~ 0 또는 그 반대) 사이의 논리 부정을 나타내기 위해 논리 다이어그램에 사용됩니다.회로 다이어그램에서 양의 논리 규약 또는 음의 논리 규약이 사용되고 있음을 주장하는 문구를 첨부해야 합니다(각각 고전압 레벨 = 1 또는 저전압 레벨 = 1).웨지는 회로 다이어그램 전체에서 균일한 컨벤션을 필요로 하지 않고 액티브-로우(저전압 레벨 = 1) 입력 또는 출력을 직접 나타내기 위해 사용됩니다.이를 직접 극성 표시라고 합니다.IEEE 규격 91/91A 및 IEC 60617-12 참조.버블과 웨지 모두 사용되는 논리 규칙에 따라 회로 다이어그램의 고유 모양과 직사각형 모양 기호에 사용할 수 있습니다.순수 논리 다이어그램에서는 버블만 의미가 있습니다. | ||||||||||||||||||||||
| 접속과 접속 | ||||||||||||||||||||||
| 그리고. | 또 ∧ B |
| ||||||||||||||||||||
| 오어 | + A + 또 B |
| ||||||||||||||||||||
| 대체부정 및 공동부정 | ||||||||||||||||||||||
| 낸드 | 는 또는 를 ¯합니다. |
| ||||||||||||||||||||
| 도 아니다 |  |  | + 또는 |
| ||||||||||||||||||
| 배타적 조건 또는 이중 조건 | ||||||||||||||||||||||
| XOR |  |  | 또 ⊻ B |
| ||||||||||||||||||
| 두 입력 값이 서로 다른 경우에만 두 입력 배타적 논리합의 출력이 참이고, 값에 관계없이 같은 경우에는 거짓입니다.입력이 두 개 이상인 경우 고유 모양 기호의 출력이 정의되지 않습니다.참 입력의 수가 정확히 하나이거나 한정 기호의 "=" 뒤에 오는 숫자일 경우 직사각형 모양 기호의 출력은 참입니다. | ||||||||||||||||||||||
| XNOR |  | 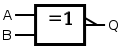 | ¯ B 또는 B |
| ||||||||||||||||||
진리표
| 인풋 | 산출량 | |
| A | 버퍼 | 인버터 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 인풋 | 산출량 | ||||||
| A | B | 그리고. | 낸드 | 오어 | 도 아니다 | XOR | XNOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | ||
| 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 0 | 1 | ||
범용 논리 게이트

찰스 샌더스 피어스(Charles Sanders Peirce, 1880-1881)는 NOR 게이트 단독(또는 NAND 게이트 단독)을 사용하여 다른 모든 논리 게이트의 기능을 재현할 수 있음을 보여주었지만 1933년까지 그의 연구는 출판되지 않았습니다.[16]최초로 출판된 증거는 Henry M에 의해서였습니다. 1913년의 셰퍼(Shefer)는 NAND 논리 연산을 셰퍼 스트로크(Shefer stroke)라고 부르기도 합니다. 논리 NOR는 Peirce's arrow라고 불리기도 합니다.[17]따라서 이러한 게이트를 유니버셜 논리 게이트라고 부르기도 합니다.[18]
| 유형 | 낸드 구축 | NOR 시공 |
|---|---|---|
| 것은 아니다. | 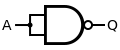 | 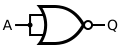 |
| 그리고. | 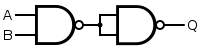 | 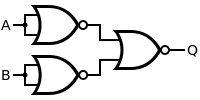 |
| 낸드 |  |  |
| 오어 |  | 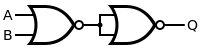 |
| 도 아니다 |  |  |
| XOR |  |  |
| XNOR |  |  |
드 모르간 등가 기호
De Morgan의 법칙을 사용하면 AND 함수는 입력과 출력이 음수인 OR 함수와 동일합니다.마찬가지로 OR 함수는 입력 및 출력이 음수인 AND 함수와 동일합니다.NAND 게이트는 입력이 네거티브된 OR 게이트와 동일하고 NOR 게이트는 입력이 네거티브된 AND 게이트와 동일합니다.
그러면 반대 코어 기호(AND 또는 OR)를 사용하지만 입력 및 출력이 음수인 기본 게이트에 대한 기호 세트가 대체됩니다.이러한 대체 기호를 사용하면 논리 회로 다이어그램을 훨씬 더 명확하게 만들 수 있으며, 능동형 고출력과 능동형 로우 입력의 우발적 연결 또는 그 반대를 보여주는 데 도움이 됩니다.양쪽 끝에 논리적 부정이 있는 연결은 부정이 없는 연결로 대체할 수 있으며 게이트를 적절히 변경하거나 그 반대로 변경할 수도 있습니다.한쪽 끝에 음수가 있고 다른 쪽 끝에 음수가 없는 연결은 대신 두 끝 중 하나에 De Morgan 등가 기호를 사용하여 해석하기 쉽게 만들 수 있습니다.연결 양 끝의 네거티브 또는 극성 표시기가 일치하면 해당 경로에 로직 네거티브가 발생하지 않으므로(효과적으로 버블 "취소") 한 심볼에서 다음 심볼로 로직 상태를 따라가기가 쉽습니다.이는 실제 논리 다이어그램에서 흔히 볼 수 있습니다. 따라서 판독기는 OR 또는 AND 도형으로만 도형을 연관시키는 습관을 들이지 말고, 표시된 "진정한" 논리 함수를 결정하기 위해 입력과 출력 모두에서 기포를 고려해야 합니다.
De Morgan 기호는 게이트의 주요 논리적 목적과 "시그널드"(활성, 온) 상태로 간주되는 노드의 극성을 더 명확하게 보여줄 수 있습니다.스위치에 의해 두 입력 NAND 게이트가 모터를 구동하는 데 사용되는 단순화된 경우를 생각해 보십시오."신호된" 상태(모터 ON)는 하나 또는 다른 스위치가 켜져 있을 때 발생합니다.AND 논리를 제시하는 일반 NAND 기호와 달리, 두 개의 음의 입력 OR 게이트인 De Morgan 버전은 OR이 관심있는 것으로 올바르게 표시합니다.일반 NAND 기호는 출력에는 버블이 있고 입력에는 버블이 없지만(모터를 켤 상태와 반대) De Morgan 기호는 모터를 구동할 극성으로 입력과 출력을 모두 표시합니다.
De Morgan의 정리는 경제적인 이유로 논리 게이트를 NAND 게이트만의 조합으로 구현하거나 NOR 게이트만의 조합으로 구현하는 데 가장 일반적으로 사용됩니다.
데이터 스토리지 및 순차 논리
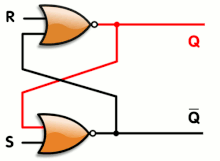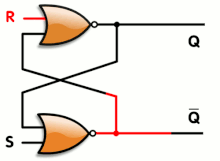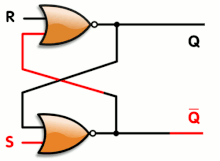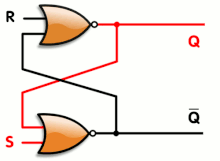
또한 로직 게이트를 사용하여 상태를 유지할 수 있으므로 데이터 저장이 가능합니다.저장 요소는 "래치" 회로에서 여러 개의 게이트를 연결하여 구성할 수 있습니다.래치 회로는 정적 랜덤 액세스 메모리에서 사용됩니다.클럭 신호를 사용하고 클럭의 상승 또는 하강 에지에서만 변경되는 더 복잡한 설계를 에지 트리거 "플립플롭"이라고 합니다.공식적으로 플립플롭은 무한히 유지할 수 있는 두 가지 안정된 상태를 가지고 있기 때문에 쌍안정 회로라고 불립니다.다중 비트 값을 저장하기 위해 여러 플립플롭을 병렬로 결합하는 것을 레지스터라고 합니다.이러한 게이트 설정을 사용하면 전체 시스템에 메모리가 있으며, 출력이 이전 상태, 즉 입력 상태의 순서에 따라 영향을 받을 수 있으므로 순차 논리 시스템이라고 합니다.대조적으로 조합 로직의 출력은 이전 입력 및 출력 상태의 영향을 받지 않고 순수하게 현재 입력의 조합입니다.
이 논리 회로는 컴퓨터 메모리에 사용됩니다.스토리지의 속도, 복잡성, 신뢰성 등의 요소에 따라 성능이 달라지며, 애플리케이션에 따라 다양한 유형의 설계가 사용됩니다.
삼상태 논리 게이트
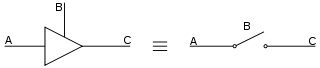
3-상태 논리 게이트는 하이(H), 로우(L) 및 하이 임피던스(Z)의 세 가지 다른 출력을 가질 수 있는 논리 게이트의 한 유형입니다.고임피던스 상태는 엄격하게 이진화된 논리에서 아무런 역할도 하지 않습니다.이 장치들은 여러 칩이 데이터를 전송할 수 있도록 CPU의 버스에 사용됩니다.적절한 제어 회로가 있는 라인을 구동하는 세 상태의 그룹은 기본적으로 멀티플렉서와 동등하며, 이 멀티플렉서는 별도의 장치 또는 플러그인 카드를 통해 물리적으로 배포될 수 있습니다.
전자 장치에서 출력이 높으면 출력이 양의 전원 단자(양의 전압)에서 전류를 소싱하고 있음을 의미합니다.출력이 낮으면 출력이 음의 전원 단자(영전압)로 싱킹 전류가 발생하고 있음을 의미합니다.임피던스가 높으면 출력이 회로에서 효과적으로 분리됩니다.
제조업
1990년대 이후 대부분의 논리 게이트는 NMOS와 PMOS 트랜지스터를 모두 사용하는 CMOS(Complementary Metal Oxide Semiconductor) 기술로 만들어졌습니다.종종 수백만 개의 논리 게이트가 단일 집적 회로에 패키징됩니다.
비전자 논리 게이트
비전자적인 구현은 다양하지만 실제 응용에 사용되는 것은 거의 없습니다.하버드 마크 I과 같은 초기 전기기계 디지털 컴퓨터는 전기기계식 릴레이를 사용하여 릴레이 로직 게이트로 제작되었습니다.논리 게이트는 분자 스케일을 포함하여, Sorteberg 릴레이 또는 기계식 논리 게이트와 같은 공압 장치를 사용하여 만들어질 수 있습니다.[19]분자(molecular logic gate)는 화학적 입력과 분광학적 출력을 기반으로 하는 다양한 형태의 기본 논리 게이트를 구성하고 있습니다.[20]논리 게이트는 DNA (DNA 나노기술 참고)[21]로 만들어졌고 마야(MAYA-II 참고)라고 불리는 컴퓨터를 만드는 데 사용되었습니다.논리 게이트는 양자역학적 효과로 만들어질 수 있습니다. 양자 논리 게이트를 참조하십시오.포토닉 로직 게이트는 비선형 광학 효과를 사용합니다.
원칙적으로 기능적으로 완전한 게이트(예를 들어 NOR 또는 NAND 게이트)로 이어지는 모든 방법은 모든 종류의 디지털 로직 회로를 만드는 데 사용될 수 있습니다.버스 시스템에 3-상태 로직을 사용할 필요는 없으며, 간단한 로직 게이트(NAND 게이트, NOR 게이트 또는 AND 및 OR 게이트 등)만 사용하여 구축할 수 있는 디지털 멀티플렉서로 대체할 수 있습니다.
논리 패밀리
RDL(저항-다이오드 로직), RTL(저항-트랜지스터 로직), DTL(다이오드-트랜지스터 로직), TTL(트랜지스터-트랜지스터 로직) 및 CMOS와 같은 다양한 특성(전력 소비, 속도, 비용, 크기)을 가진 여러 로직 제품군이 있습니다.또한 여전히 CMOS 기술을 사용하는 표준 CMOS 로직 대 고급 타입과 같은 하위 변형이 있지만 더 느린 PMOS 트랜지스터로 인한 속도 손실을 방지하기 위한 몇 가지 최적화가 있습니다.
참고 항목
참고문헌
- ^ Jaeger (1997). Microelectronic Circuit Design. McGraw-Hill. pp. 226–233. ISBN 0-07-032482-4.
- ^ Kanellos, Michael (2003-02-11). "Moore's Law to roll on for another decade". CNET. 집적 회로로부터
- ^ Tinder, Richard F. (2000). Engineering digital design (2nd ed.). pp. 317–319. ISBN 0-12-691295-5.
- ^ Rowe, Jim. "Circuit Logic – Why and How". No. December 1966. Electronics Australia.
- ^ Nylan, Michael (2001). The Five "Confucian" Classics. Yale University Press. pp. 204–206. ISBN 978-0-300-08185-5. Retrieved 2010-06-08.
- ^ Perkins, Franklin (2004). "Exchange with China". Leibniz and China: A Commerce of Light. Cambridge University Press. p. 117. ISBN 9780521830249.
... one of the traditional orderings of the hexagrams, the xiantian tu ordering made by Shao Yong, was, with a few modifications, the same order found in Leibniz's binary arithmetic.
- ^ 피어스, CS, "A에게 보내는 편지, 피어스. 마르콴드", 1886년 날짜, 찰스 S. Peirce, v. 5, 1993, pp. 420–423 참조
- ^ Yamada, Akihiko (2004). "History of Research on Switching Theory in Japan". IEEJ Transactions on Fundamentals and Materials. Institute of Electrical Engineers of Japan. 124 (8): 720–726. doi:10.1541/ieejfms.124.720.
- ^ "Switching Theory/Relay Circuit Network Theory/Theory of Logical Mathematics". IPSJ Computer Museum. Information Processing Society of Japan.
- ^ Stanković, Radomir S.; Astola, Jaakko T.; Karpovsky, Mark G. (2007). Some Historical Remarks on Switching Theory. CiteSeerX 10.1.1.66.1248.
- ^ a b Stanković, Radomir S. [in German]; Astola, Jaakko Tapio [in Finnish], eds. (2008). Reprints from the Early Days of Information Sciences: TICSP Series On the Contributions of Akira Nakashima to Switching Theory (PDF). Tampere International Center for Signal Processing (TICSP) Series. Vol. 40. Tampere University of Technology, Tampere, Finland. ISBN 978-952-15-1980-2. ISSN 1456-2774. Archived from the original (PDF) on 2021-03-08.Stanković, Radomir S. [in German]; Astola, Jaakko Tapio [in Finnish], eds. (2008). Reprints from the Early Days of Information Sciences: TICSP Series On the Contributions of Akira Nakashima to Switching Theory (PDF). Tampere International Center for Signal Processing (TICSP) Series. Vol. 40. Tampere University of Technology, Tampere, Finland. ISBN 978-952-15-1980-2. ISSN 1456-2774. Archived from the original (PDF) on 2021-03-08.
{{cite book}}CS1 메인 : 위치 누락 게시자 (링크) (3+207+1페이지) 10:00 min - ^ Lojek, Bo (2007). History of Semiconductor Engineering. Springer. pp. 321–323. ISBN 978-3-54034258-8.
- ^ "1963: Complementary MOS Circuit Configuration is Invented". Computer History Museum. Retrieved 2019-07-06.
- ^ "Graphical Symbols for Logic Diagrams". ASSIST Quick Search. Defense Logistics Agency. MIL-STD-806. Retrieved 2021-08-27.
- ^ a b "Overview of IEEE Standard 91-1984 Explanation of Logic Symbols" (PDF). Texas Instruments Semiconductor Group. 1996. SDYZ001A.
- ^ Peirce, C. S. (1880-1881년 겨울의 원고), "상수가 하나인 불리언 대수", 1933년 Collected Papers v. 4, 문단 12-20에 발표.1989년 찰스 S의 글로 재인쇄됨. Peirce v. 4, pp. 218–221, Google [1] 참조
- ^ Büning, Hans Kleine; Lettmann, Theodor (1999). Propositional logic: deduction and algorithms. Cambridge University Press. p. 2. ISBN 978-0-521-63017-7.
- ^ Bird, John (2007). Engineering mathematics. Newnes. p. 532. ISBN 978-0-7506-8555-9.
- ^ Merkle, Ralph C. (1993). "Two Types of Mechanical Reversible Logic". Xerox PARC.
- ^ Erbas-Cakmak, Sundus; Kolemen, Safacan; Sedgwick, Adam C.; Gunnlaugsson, Thorfinnur; James, Tony D.; Yoon, Juyoung; Akkaya, Engin U. (2018). "Molecular logic gates: the past, present and future". Chemical Society Reviews. 47 (7): 2228–2248. doi:10.1039/C7CS00491E. hdl:11693/50034. ISSN 0306-0012. PMID 29493684.
- ^ Stojanovic, Milan N.; Mitchell, Tiffany E.; Stefanovic, Darko (2002). "Deoxyribozyme-Based Logic Gates". Journal of the American Chemical Society. 124 (14): 3555–3561. doi:10.1021/ja016756v. PMID 11929243.
추가열람
- Awschalom, D. D.; Loss, D.; Samarth, N. (2002). Semiconductor Spintronics and Quantum Computation. Springer. ISBN 978-3-540-42176-4.
- Bostock, Geoff (1988). Programmable logic devices: technology and applications. McGraw-Hill. ISBN 978-0-07-006611-3.
- Brown, Stephen D.; Francis, Robert J.; Rose, Jonathan; Vranesic, Zvonko G. (1992). Field Programmable Gate Arrays. Kluwer Academic. ISBN 978-0-7923-9248-4.
외부 링크
 Wikimedia Commons의 Logic gate 관련 미디어
Wikimedia Commons의 Logic gate 관련 미디어












