무질서 산란
Chaotic scattering무질서한 산란은 초기 조건에 강한 민감성을 보이는 산란계를 다루는 혼돈 이론의 한 분야다.고전적 산란 시스템에는 하나 이상의 충격 매개변수 b가 있을 것이며, 이 매개변수는 입자가 산란기로 보내진다.이것은 입자가 무한을 향해 나갈 때 하나 이상의 출구 매개변수 y를 발생시킨다.입자가 시스템을 가로지르는 동안, T(입자가 시스템을 나가는 데 걸리는 시간)는 이동 거리 외에, s, 즉 특정 시스템에서는 입자가 단단하고 고정된 물체와 무손실 충돌을 겪는 "빌리어드 유사" 시스템에서는 두 개가 동등할 것이다(아래 참조).혼란스러운 산란계에서는 충격 매개변수의 미세한 변화가 출구 매개변수에 매우 큰 변화를 일으킬 수 있다.
가스파드-리스 시스템
훌륭한 예시 시스템은 "가스퍼드-쌀" (GR) 산란 시스템 - 단순히 "쓰리-디스크" 시스템이라고도 알려져 있는데, 이것은 혼란스러운 산란에서 많은 중요한 개념을 구체화하면서도 이해하기 쉽고 시뮬레이션이 용이하다.개념은 매우 간단하다: 우리는 세 개의 하드디스크를 삼각형 형태로 배열하고, 포인트 입자가 보내져서 무한대로 빠져나갈 때까지 완벽하고 탄성 있는 충돌을 겪는다.이 논의에서, 우리는 GR 시스템이 정삼각형의 점들에 따라 균등하게 간격을 두고 동일한 크기의 디스크를 갖는 것을 고려할 것이다.
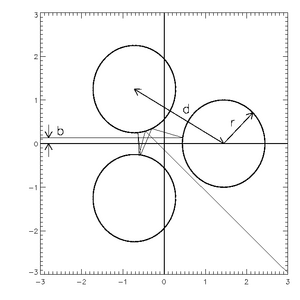
그림 1은 이 시스템을 보여주고, 그림 2는 두 가지 예시 궤적을 보여준다.먼저 궤적이 마지막으로 빠져나가기 전에 일정 시간 동안 시스템 주위를 공전한다는 점에 유의하십시오.또한, 충격 매개변수를 왼쪽의 완벽한 수평선 두 개의 시작(시스템은 완전히 되돌릴 수 있다: 출구 지점도 진입점이 될 수 있다)으로 간주할 경우, 두 궤적은 초기에는 거의 동일할 정도로 근접하다.그들이 퇴장할 때쯤에는 완전히 달라져 초기 조건에 대한 강한 민감성을 보여준다.이 시스템은 기사 전반에 걸쳐 예시로 사용될 것이다.
붕괴율
균일하게 분포된 충격 매개변수를 가진 다수의 입자를 도입하면, 입자가 시스템에서 빠져나가는 속도를 붕괴율이라고 한다.많은 시행에 걸쳐 시스템을 시뮬레이션하고 지연시간 히스토그램을 구성함으로써 붕괴율을 계산할 수 있다.GR 시스템의 경우, 지연 시간과 입자 궤적 길이는 곱셈 계수의 경우 등가지만 동일하다는 것을 쉽게 알 수 있다.충격 매개변수에 대한 일반적인 선택은 Y 좌표인 반면 궤적 각도는 0도(수평)로 일정하게 유지된다.한편, 우리는 이 입자가 일단 경계를 통과하면, 시스템 중심에서 임의로, 그러나 충분히 큰 거리를 지나게 되면, "시스템에서 빠져나왔다"고 말한다.
시스템에 남아 있는 입자의 수 N(T)은 다음과 같이 달라질 것으로 예상한다.
따라서 붕괴율인 은 다음과 같이 주어진다.
여기서 n은 총 입자 수입니다.[2]
그림 3은 무작위 충격 매개변수로 시작된 백만 개의 입자(1e6)의 시뮬레이션을 위한 경로 길이 대 입자 수의 그림을 보여준다. b. 음의 기울기의 적합 직선 = = 이 겹쳐진다.경로 길이 s는 (정수) 속도를 적절히 조절할 경우 붕괴 시간 T와 동등하다.지수 붕괴율은 특히 쌍곡선 무질서한 산란의 속성이다.비열정적 비열정적 비열정적 비열정적 비열정적 산술적 붕괴율을 가질 수 있다.[3]
실험시스템과 안정다지관

그림 4는 포인트 입자 대신 레이저를 사용해 가스파드-라이스 시스템을 실험적으로 실현한 것이다.실제로 이것을 시도해 본 사람이라면 누구나 알고 있듯이, 이것은 시스템을 테스트하는 데 그다지 효과적인 방법이 아니다. 즉 레이저 빔이 사방으로 흩어진다.스위트, Ott 및 요크에서 알 수 있듯이, 보다 효과적인 방법은 디스크 사이의 간격(또는 이 경우 실린더 쌍에 걸쳐 테이프로 색칠된 종이 조각)을 통해 색광을 유도하고 열린 간격을 통해 반사를 보는 것이다.그 결과는 아래와 같이 아래의 시뮬레이션 버전에서 보다 명확하게 볼 수 있는 교대 색의 복잡한 패턴이다.
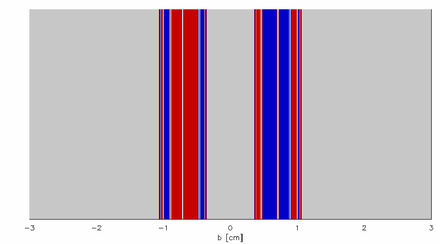
그림 5와 6은 각 충격 매개변수 b에 대한 끌어당김의 기저, 즉 주어진 b 값에 대해 입자가 어느 틈새를 통해 빠져나가는가?분지 경계는 칸토어(Cantor)를 형성하고 안정적 다지관의 구성원을 나타낸다. 즉, 일단 시작되면 시스템을 빠져나가지 않는 궤적이다.

불변 집합과 상징적 역학

대칭인 이상 우리는 시스템을 혼란스럽고 역동적인 시스템을 나타내는 일반적인 방법인 반복 함수 맵으로 쉽게 생각할 수 있다.[7] Figure 7 shows one possible representation of the variables, with the first variable, , representing the angle around the disc at rebound and the second, , representing the impact/rebound angle relative to원반불변성 집합이라고 불리는 이 두 변수들의 하위 집합은 그들 자신에게 매핑될 것이다.그림 8과 9에 표시된 4개의 멤버는 프랙탈이며, 전혀 매력적이지 않으며 측정값 0이 될 것이다.이것은 프랙탈 불변성 집합이 끌어당기고 실제로 유인력의 분지를 구성하는 더 일반적으로 논의되는 혼돈 시스템의 흥미로운 반전이다.불변 집합의 전혀 매력적이지 않은 성질은 쌍곡 혼돈 산란자의 또 다른 속성이라는 점에 유의한다.
불변 세트의 각 멤버는 심볼 역학을 사용하여 모델링할 수 있다. 즉, 궤적은 리바운드되는 각 디스크에 기초하여 라벨로 표시된다.그러한 모든 시퀀스의 집합은 셀 수 없는 집합을 형성한다.[8]그림 8과 9에 표시된 4명의 구성원에 대해 상징 역학은 다음과 같다.
...121212121212... ...232323232323... ...313131313131... ...123123123123...
각 시퀀스에 출발점이 있다는 점을 제외하고, 안정 다지관의 구성원도 마찬가지로 표현될 수 있다.불변 집합의 구성원이 두 유인력의 기저 사이의 경계에 "적합"해야 한다는 점을 고려할 때, 만약 혼란에 빠지면 궤적이 시퀀스를 따라 어느 곳으로든 빠져나갈 수 있다는 것이 명백하다.따라서 주어진 경계선 사이에 세 가지 "색상"의 교차 분지가 무한히 존재할 것이라는 점도 분명히 보여야 한다.[2][3][8]
불안정한 성격 때문에 불변 세트나 안정 다지관의 멤버에 직접 접근하기 어렵다.불확도 지수는 이러한 유형의 시스템의 프랙탈 치수를 측정하도록 이상적으로 맞춤화된다.단일 임팩트 파라미터 b를 다시 한 번 사용하여 랜덤 임팩트 파라미터로 여러 번의 실험을 수행하여 , 을(를 분 단위로 교란시키고 디스크에서 나오는 리바운드 수, 즉 불확실성 분율의 변화 빈도를 계산한다.시스템이 2차원이라 하더라도 단일 충격 매개변수는 안정적인 다지관의 프랙탈 치수를 측정하기에 충분하다는 점에 유의하십시오.이는 이중 임팩트 파라미터의 함수로 플로팅된 끌어당김의 기저인 과 {{\}을(를) 나타낸 그림 10에 나타나 있다 바진 사이의 경계에서 볼 수 있는 안정적 다지관은 한 차원만을 따라 프랙탈이다.
그림 11은 불확실성의 함수로써 시뮬레이션 가스파드-라이스 시스템에 대한 을(를) 나타낸다.The slope of the fitted curve returns the uncertainty exponent, , thus the box-counting dimension of the stable manifold is, . The invariant set is the intersection of the stable and unstable manifolds.[9]
시스템은 앞쪽으로 달리든 뒤쪽으로 달리든 동일하기 때문에 불안정한 다지관은 단순히 안정 다지관의 거울상일 뿐이며 프랙탈 치수는 동일할 것이다.[8] 이를 바탕으로 불변량 집합의 프랙탈 치수를 계산할 수 있다.[2]
여기서 D_s와 D_u는 각각 안정적이고 불안정한 다지관의 프랙탈 치수이며, N=2는 시스템의 치수성이다.불변 집합의 프랙탈 치수는 D=1.24이다.

프랙탈 치수, 붕괴율 및 랴푸노프 지수 사이의 관계
앞의 논의로부터 붕괴율, 프랙탈 치수, 랴푸노프 지수가 모두 연관되어 있다는 것을 분명히 해야 한다.예를 들어, 큰 랴푸노프 지수는 우리에게 불변 집합의 궤적이 흔들릴 경우 얼마나 빠르게 갈릴지 알려준다.마찬가지로 프랙탈 치수는 불변 집합의 궤도의 밀도에 대한 정보를 우리에게 줄 것이다.따라서 우리는 이차원 산란계에 대한 다음과 같은 추측에서 포착된 두 가지 모두 붕괴율에 영향을 줄 것을 알 수 있다.[2]
여기서 D는1 정보 차원이고 h와1 h는2 각각 작은 랴푸노프 지수 및 큰 랴푸노프 지수다.유인자의 경우 = 을(를) 표시하면 Kaplan–로 줄어든다.요크 추측.[2]
참고 항목
참조
- ^ Gaspard, Pierre; Rice, Stuart A. (1989-02-15). "Scattering from a classically chaotic repellor". The Journal of Chemical Physics. AIP Publishing. 90 (4): 2225–2241. doi:10.1063/1.456017. ISSN 0021-9606.
- ^ a b c d e Edward Ott (1993). Chaos in Dynamical Systems. Cambridge University Press.
- ^ a b c Yalçinkaya, Tolga; Lai, Ying-Cheng (1995). "Chaotic Scattering". Computers in Physics. AIP Publishing. 9 (5): 511-518. doi:10.1063/1.168549. ISSN 0894-1866.
- ^ a b c Peter Mills (2000). An Experimental Classical Chaotic Scattering System Investigated (Technical report). University of Waterloo.
- ^ David Sweet, Edward Ott and James A. Yorke. "Complex Topology in Chaotic Scattering: A Laboratory Observation". Nature. 399: 313.
- ^ a b Peter Mills (1998). Noisy Chaotic Scattering (Thesis). University of Waterloo.
- ^ Denny Gulick (1992). Encounters with Chaos. McGraw–Hill.
- ^ a b c Bleher, Siegfried; Grebogi, Celso; Ott, Edward (1990). "Bifurcation to chaotic scattering". Physica D: Nonlinear Phenomena. Elsevier BV. 46 (1): 87–121. doi:10.1016/0167-2789(90)90114-5. ISSN 0167-2789.
- ^ Ott, Edward; Tél, Tamás (1993). "Chaotic scattering: An introduction" (PDF). Chaos: An Interdisciplinary Journal of Nonlinear Science. AIP Publishing. 3 (4): 417–426. doi:10.1063/1.165949. ISSN 1054-1500. PMID 12780049.




 겹쳐진다.경로 길이 s는 (정수) 속도를 적절히 조절할 경우 붕괴 시간 T와 동등하다.지수 붕괴율은 특히 쌍곡선 무질서한 산란의 속성이다.비열정적 비열정적 비열정적 비열정적 비열정적 산술적 붕괴율을 가질 수 있다.
겹쳐진다.경로 길이 s는 (정수) 속도를 적절히 조절할 경우 붕괴 시간 T와 동등하다.지수 붕괴율은 특히 쌍곡선 무질서한 산란의 속성이다.비열정적 비열정적 비열정적 비열정적 비열정적 산술적 붕괴율을 가질 수 있다.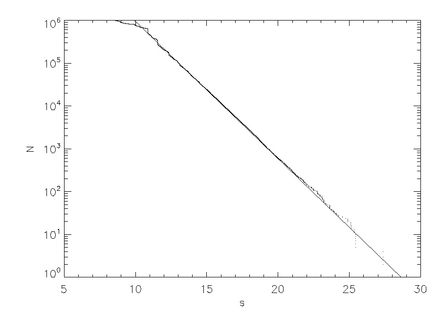
![\theta \in [-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb953905c1f4461b83fe73f5a00e751727ddd73b)
![\phi \in [-\pi /2,\pi /2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cde2ad5af060b602ccfcf027c34dfd11642cb703)



 {
{








