링 카운터
Ring counter링 카운터는 시프트 레지스터에 연결된 플립 플랍으로 구성된 카운터 유형으로, 마지막 플립 플랍의 출력이 첫 번째 플립 플랍의 입력에 공급되어 "원형" 또는 "링" 구조를 만듭니다.
링 카운터에는 다음 두 가지 유형이 있습니다.
- 원핫 카운터라고도 하는 스트레이트 링 카운터는 마지막 시프트 레지스터의 출력을 첫 번째 시프트 레지스터 입력에 연결하고 단일 1(또는 0) 비트를 링 주위에 순환시킵니다.
- 스위치 테일링 카운터, 워킹링 카운터, 존슨 카운터 또는 뫼비우스 카운터라고도 불리는 트위스트링 카운터는 마지막 시프트 레지스터 출력의 보완을 첫 번째 레지스터의 입력에 연결하고 1의 스트림을 순환시킨 후 링 주위에 0을 순환시킵니다.
4비트 링 카운터 시퀀스
| 스트레이트 링 카운터 | 존슨 카운터 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 주 | 문제 0 | 문제 1 | 문제 2 | 문제 3 | 주 | 문제 0 | 문제 1 | 문제 2 | 문제 3 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 2 | 1 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 4 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 5 | 0 | 1 | 1 | 1 | |
| 2 | 0 | 0 | 1 | 0 | 6 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
특성.
링 카운터는 하드웨어 설계(ASIC 및 FPGA 설계 등)에서 유한 상태 머신을 작성하기 위해 자주 사용됩니다.바이너리 카운터는 링 카운터보다 상당히 복잡하고 비트 수가 증가함에 따라 전파 지연이 커지는 가산기 회로를 필요로 하지만 링 카운터의 전파 지연은 코드 내의 비트 수에 관계없이 거의 일정합니다.
직선 형태와 뒤틀린 형태는 다른 특성, 그리고 상대적인 장점과 단점을 가지고 있습니다.
링 카운터의 일반적인 단점은 스테이트 번호의 통상적인 바이너리 부호화보다 밀도가 낮은 코드라는 것입니다.바이너리 카운터는 2^N 상태를 나타낼 수 있습니다.여기서 N은 코드의 비트수이며, 스트레이트 링 카운터는 N개의 상태만을 나타낼 수 있으며, Johnson 카운터는 2N 상태만을 나타낼 수 있습니다.이는 레지스터가 조합 로직보다 더 비싼 하드웨어 구현에서 중요한 고려 사항일 수 있습니다.
Johnson 카운터가 권장되는 경우가 있습니다.이는 동일한 수의 시프트 레지스터에서2배의 카운트 상태를 제공하며 시작 시 첫 번째 카운트 비트를 외부로 주입하지 않고도 전체 제로 상태에서 자기 초기화할 수 있기 때문입니다.Johnson 카운터는 그레이 코드와 같이 인접 상태가 1비트(즉, Hamming 거리가 1비트)만 다른 코드를 생성합니다.이 코드는 비트 패턴을 [1]비동기적으로 샘플링하는 경우에 도움이 됩니다.
일부 시퀀스 컨트롤러와 같이 카운터 상태를 완전 디코딩 또는 원핫으로 표현해야 할 경우 스트레이트링 카운터가 우선됩니다.One-hot 속성은 코드 세트가 최소 Hamming 거리 [2]2만큼 분리되므로 단일 비트 오류를 감지할 수 있습니다(1비트를 켜고 1비트를 끄는 것 이외 오류 패턴).
양방향 또는 업다운링 카운터를 작성하기 [3]위해 (멀티플렉서를 사용하여 왼쪽 또는 오른쪽 네이버에서 각 플립플랍의 입력을 취득) 양방향 시프트 레지스터가 사용되는 경우가 있습니다.
논리도
스트레이트 링 카운터는 다음과 같은 논리 구조를 가지고 있습니다.
리셋 라인이 초기 원핫 패턴을 설정하는 대신, 스트레이트 링은 마지막을 제외한 모든 출력에 걸쳐 분산된 피드백 게이트를 사용하여 자기 초기화되므로 마지막 [4]이외의 어느 단계에 1이 없을 때 입력에 1이 제시된다.
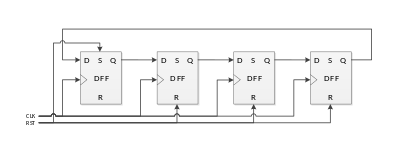
Robert Royce Johnson의 이름을 딴 Johnson 카운터는 반전 링입니다.다음은 4비트 Johnson 카운터입니다.
첫 번째 D 입력으로 피드백하기 전에 마지막 시프트 레지스터의 Q 신호 반전을 나타내는 작은 버블에 주목하여 Johnson 카운터가 됩니다.
역사
디지털 컴퓨팅의 시대 이전에는 디지털 카운터가 알파 및 베타 입자에 대한 방사성 붕괴와 같은 랜덤 이벤트의 비율을 측정하는 데 사용되었습니다.고속의 「프리 스케일링」카운터는 랜덤이벤트 레이트를 관리 용이성과 통상의 레이트로 낮춥니다.C. E. Wynn-Williams에 [5]의해 개발된 것과 같이 1940년 이전에 10년(10승)의 스케일러를 만들기 위해 5개의 상태의 링 카운터가 2개의 스케일러와 함께 사용되었습니다.
초기 링 카운터는 국소 쌍안정 플립 플랍이 아닌 글로벌 피드백에 의존하여 스테이지당 1개의 활성 소자(진공 튜브, 밸브 또는 트랜지스터)만을 사용하여 1941년 Robert E 특허 출원 등 1개의 핫 상태 이외의 상태를 억제했습니다. 국립 현금 등록 [6]회사의 어머니.윌콕스 P. 오버벡은 하나의 진공 [7][8]튜브에 여러 개의 양극을 사용하는 버전을 발명했다. 그의 업적을 인정받아 링 카운터는 때때로 "오버벡 링"[9][10]이라고 불린다(그리고 2006년 이후에는 "오버벡 카운터"라고 불리기도 한다. 위키피디아는 2006년부터 2018년까지 이 용어를 사용했다).
ENIAC에서는 10스테이트의 원핫링 카운터에 근거한 10진수 계산이 사용되었습니다.NCR의 Mumma와 MIT의 Overbeck의 작품은 ENIAC [11]기술에 대한 J. Presper Eckert와 John Mauchly의 특허를 무효화하면서 특허청에 의해 심사된 선행 예술 작품 중 하나이다.
1950년대에는 스테이지당 2관 또는 트윈 트라이오드의 플립 플랍이 있는 링 카운터가 [12]등장했습니다.
Robert Royce Johnson은 가장 간단한 피드백 논리로 다른 수의 주를 만들 목적으로 많은 다른 시프트 레지스터 기반 카운터를 개발하여 [13]1953년에 특허를 출원했습니다.Johnson 카운터는 이 중 가장 단순합니다.
응용 프로그램
로 계측기 암호 해독(황야를 로빈슨 codebreaking기에 예를 들어, 로도스 컴퓨터)[14]에 패턴 작업에서 세는 방법으로 주파수 prescalers고 소수 점 컴퓨터와 계산기에서를 사용하여 산수에 카운터 요소accumulator(가이거 계산기와 같은 악기들을 위한 예)[5]반지 카운터의 초기 응용 프로그램 있었다. 어느 하나2진수(콜로소스와 같은) 또는 10주 원핫(ENIAC와 같은) 표현.
스트레이트 링 카운터는 에 대해 완전히 디코딩된 원핫코드를 생성합니다.이 코드는 사이클 제어 사이클의 각 상태에서 특정 액션을 활성화하기 위해 자주 사용됩니다.또한 Johnson 카운터에서 각 [15][nb 1]상태에 대해 게이트를 하나씩 사용하여 원핫 코드를 디코딩할 수도 있습니다.
Johnson 카운터는 단일 핫코드 및 주파수 프리스케일러를 생성하는 효율적인 대체 방법일 뿐만 아니라 그레이 [16]코드처럼 한 번에 1비트만 변경되므로 글리치 없이 비동기적으로 샘플링할 수 있는 짝수 상태의 사이클을 인코딩하는 간단한 방법입니다.초기 컴퓨터 마우스는 2차원 각각에서 움직임을 나타내기 위해 상향식(양방향) 2비트 존슨 또는 회색 인코딩을 사용했지만, 마우스에서는 그러한 코드가 플립 플랍의 링에 의해 생성되지 않았다(대신 전자 기계식 또는 광학 직교 [17]인코더에 의해 생성되었다).2비트 Johnson 코드와 2비트 Gray 코드는 동일하지만 3비트 이상의 경우 Gray 코드와 Johnson 코드가 다릅니다.5비트의 경우 코드는 10진수의 [18][19][20][21][22][23][24][25]Libaw-Craig 코드 [와 동일합니다.
Johnson 카운터라고도 하는 워킹 링 카운터 및 몇 개의 저항기를 사용하면 사인파의 글리치 없는 근사치를 생성할 수 있습니다.조정 가능한 프리스케일러와 결합할 경우, 이는 아마도 가장 간단한 수치 제어 오실레이터일 것입니다.이러한 2개의 워킹링 카운터는 듀얼톤 멀티주파수 시그널링 및 초기 모뎀톤에서 [26]사용되는 연속 위상 주파수 시프트 키잉을 생성하는 가장 간단한 방법입니다.
|
|
|
|
|
|
|
|
「 」를 참조해 주세요.
메모들
- ^ 이러한 방식으로 디코딩된 단일 상태의 Johnson 카운터 회로는 원래 IBM MDA 및 CDA 비디오 디스플레이 어댑터 설계에서 타이밍 시퀀서 로직으로 확인할 수 있습니다. 하나 또는 두 개의 74x174 16진수 D-플립 플랍 IC는 시프트 레지스터로 배선되어 존슨 카운터 및 2입력 NAND 게이트(MOR 게이트)를 형성합니다.CGA)는 +RAS(Row Address Strobe [to DRAM]) 및 S/-L(Shift/NOT Load)과 같은 신호로 사용되는 상태를 디코딩하는 데 사용됩니다.출처:IBM 퍼스널 컴퓨터 옵션 및 어댑터 테크니컬 레퍼런스, 흑백 디스플레이 및 프린터 어댑터, 로직 다이어그램, IBM 퍼스널 컴퓨터 옵션 및 어댑터 테크니컬 레퍼런스, 컬러 그래픽스 모니터 어댑터, 로직 다이어그램.
레퍼런스
- ^ Pedroni, Volnei A. (2013). Finite State Machines in Hardware: Theory and Design. MIT Press. p. 50. ISBN 978-0-26201966-8.
- ^ Mengibar, Luis; Entrena, Luis; Lorenz, Michael G.; Sánchez-Reillo, Raúl (2003). "State Encoding for Low-Power FSMs in FPGA". Integrated Circuit and System Design. Power and Timing Modeling, Optimization and Simulation: Proceedings of the 13th International Workshop, PATMOS 2003, Torino, Italy, 10–12 September 2003. Vol. 13. Springer Science & Business Media. p. 35. ISBN 9783540200741.
- ^ Stan, Mircea R. (1997). "Synchronous up/down counter with clock period independent of counter size" (PDF). Proceedings 13th IEEE Symposium on Computer Arithmetic: 274–281.
- ^ Holdsworth, Brian; Woods, Clive (2002). Digital Logic Design (4 ed.). Newnes Books / Elsevier Science. pp. 191–192. ISBN 0-7506-4588-2. Retrieved 2020-04-19.
{{cite book}}: CS1 maint: 무시된 ISBN 오류(링크) CS1 maint: url-status(링크)(519페이지) [1] - ^ a b Lewis, Wilfrid Bennett (1942). Electrical Counting: With Special Reference to Counting Alpha and Beta Particles. Cambridge University Press. p. 90. ISBN 9781316611760.
- ^ "전자 축적", 로버트 E.1941년 출원된 어머니의 미국 특허 제2405096호
- ^ "전자 전환 장치", Wilcox P.1943년에 제출된 오버벡의 미국 특허 제2427533호
- ^ Dayton Codebreakers: 1942년 연구 보고서, "Overbeck씨의 새로운 고속 카운터, 1942년 1월 8일"을 언급했다.
- ^ RAMAC 305 - IBM Customer Engineering Manual of Instruction (PDF). IBM. 1959.
[…] The Overbeck ring is used to supply timed pulses within computer circuits much as cam operated circuit breakers supply timed pulses on mechanical machines. It consists of a set of triggers with a common input from the ring drive line which carries pulses supplied by the process drum. […] Initially the triggers are reset OFF with the exception of the home trigger, which is ON. Each negative input pulse will turn OFF the trigger that is ON. The fall of the voltage at pin 10 of the trigger being turned OFF will grid flip the next trigger ON. This continues through a closed ring […]
- ^ Electrical Technology - A Suggested 2-Year Post High School Curriculum. Technical Education Program Series. United States, Division of Vocational and Technical Education. 1960. p. 52.
- ^ Randall, Brian (2014). "The Origins of Digital Computers: Supplementary Bibliography". In Metropolis, Nicholas (ed.). History of Computing in the Twentieth Century. Elsevier. pp. 651–652. ISBN 9781483296685.
- ^ William Alfred Higinbotham, "고속 임펄스 회로", 미국 특허 제2536808호, 1949년 출원
- ^ Robert Royce Johnson, "전자 카운터", 미국 특허 번호 3030581은 1953년에 제출되었습니다.
- ^ Copeland, B. Jack (2010). Colossus: The Secrets of Bletchley Park's Code-breaking Computers. Oxford University Press. pp. 123–128. ISBN 978-0-19957814-6.
- ^ Langholz, Gideon; Kandel, Abraham; Mott, Joe L. (1998). Foundations of Digital Logic Design. World Scientific. pp. 525–526. ISBN 978-9-81023110-1.
- ^ 반 Holten, 코르넬리우스(8월 1982년).델프트 공과 대학교, 델프트, 네덜란드에서 쓰여진."대칭 출력과 디지털 분할 컴퍼스.-그 작가는 시각 펄스의 대칭과 모서리 구역을 통제되고 있는 피드백으로 존슨 카운터를 사용한다"(PDF).와이어리스 월드.Vol88, 안 돼 1559년.서튼, 서리, 영국:IPC비즈니스 프레스 회사를 대신하여 서명함. 43–46.ISSN 0043-6062.그 2021-02-21에 원래에서Archived(PDF).2021-02-20 Retrieved.[2][3](4장)
- ^ 올림피크 리옹, 리차드 F.(1981년 8월), 그 광학 마우스, 건축 방법론 스마트 디지털 Sensors에(보고서)(PDF), 팔로 알토 연구 센터, 캘리포니아 팔로 알토의 USA:제록스, VLSI81-1, 원본에서 2020-05-23에, 단순히 수, 그 계산기 X, Y를 위해 필요한 4개 주 2020-05-23 회수된(PDF)에서 보관하고 있다. 어느 쪽이든 방향(위 또는 아래로), 시간(즉, 00,01,11,10)에 조금도 변하고 있습니다.[Gray-code용 카운터 나 존슨 카운터(뫼비우스 계수기)의 이것은 단순한 경우다.(41페이지)
- ^ Libaw, William H.; Craig, Leonard J. (October 1953) [September 1953]. "A Photoelectric Decimal-Coded Shaft Digitizer". Transactions of the I.R.E. Professional Group on Electronic Computers. EC-2 (3): 1–4. doi:10.1109/IREPGELC.1953.5407731. eISSN 2168-1759. ISSN 2168-1740. Retrieved 2020-05-26. (4페이지)
- ^ 파월, E. 알렉산더(6월 1968년)."충족하는 것 특히 아날로그의 디지털 변환에 유용한".Fluidic 제어 회선(PDF)에게 유용한 코드에 관한 짧은 노트.Cranfield, 영국:대학 항공회과 생산 공학의. 페이지의 주 10.S2CID 215864694.CoAMemo156.그 2020-12-15에 원래에서Archived(PDF)..(18페이지)(NB2020-12-15 Retrieved.이 문서에서는 그레이 코드를 수정한 Glixon 코드를 명명하고 Richard W. Hamming의 이름을 잘못 표기하고 있습니다.)
- ^ Dokter, Folkert, Steinhauer, 위르겐(1973-06-18).디지털 전자입니다.필립스 기술 도서관(주요 표적 지역선)/맥밀런 교육(1영어 교육의 Reprint.).아인트호벤, 네덜란드:그 맥밀란 출판 주식 회사/N.V필립스의 Gloeilampenfabrieken. 페이지의 주 43.doi:10.1007/978-1-349-01417-0.아이 에스비엔 978-1-349-01419-4.SBN 333-13360-9..(270페이지)2020-05-11 Retrieved
- ^ Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). Vol. I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. pp. 52, 58, 98. ISBN 3-87145-272-6. (102+327+3페이지)
- ^ Dokter, Folkert; Steinhauer, Jürgen (1975) [1970]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Anwendung der digitalen Grundschaltungen und Gerätetechnik. Philips Fachbücher (in German). Vol. II (4th ed.). Hamburg, Germany: Deutsche Philips GmbH. p. 169. ISBN 3-87145-273-4. (xi+393+3페이지)
- ^ Steinbuch, Karl W., ed. (1962). Written at Karlsruhe, Germany. Taschenbuch der Nachrichtenverarbeitung (in German) (1 ed.). Berlin / Göttingen / New York: Springer-Verlag OHG. pp. 71–72, 74. LCCN 62-14511.
- ^ Steinbuch, Karl W.; Wagner, Siegfried W., eds. (1967) [1962]. Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. LCCN 67-21079. Title No. 1036.
- ^ Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik – Band II – Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (in German). Vol. 2 (3 ed.). Berlin, Germany: Springer Verlag. ISBN 3-540-06241-6. LCCN 73-80607.
- ^ 돈 랭커스터.'TV 타자기 쿡북'.1976년 페이지 180-181